K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 8 2021
30.
Đường tròn tâm \(I\left(8;3\right)\) bán kính \(R=\sqrt{7}\)
ẢNh của đường tròn qua phép tịnh tiến là đường tròn có tâm \(\left\{{}\begin{matrix}x'=8+5=13\\y'=3+7=10\end{matrix}\right.\) và bán kính R
Phương trình:
\(\left(x-13\right)^2+\left(y-10\right)^2=7\)
8.
Do \(\overrightarrow{DA}=\overrightarrow{CB}\) nên phép tịnh tiến vecto \(\overrightarrow{DA}\) biến C thành B
9.
\(\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AC}\) nên phép tịnh tiến \(T_{\overrightarrow{AB}+\overrightarrow{AD}}\) biến A thành C
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 8 2021
10.
Phép tịnh tiến \(\overrightarrow{AB}\) biến d thành tiếp tuyến tại B
11.
\(\overrightarrow{BC}=\left(-6;-3\right)\)
Gọi G là trọng tâm tam giác ABC
\(\Rightarrow\left\{{}\begin{matrix}x_G=\dfrac{x_A+x_B+x_C}{3}=2\\y_G=\dfrac{y_A+y_B+y_C}{3}=1\end{matrix}\right.\)
\(\Rightarrow G\left(2;1\right)\)
G' là ảnh của G qua phép tịnh tiến \(\overrightarrow{BC}\)
\(\Rightarrow\left\{{}\begin{matrix}x_{G'}=-6+2=-4\\y_{G'}=-3+1=-2\end{matrix}\right.\)
\(\Rightarrow G'\left(-4;-2\right)\)
AH
Akai Haruma
Giáo viên
26 tháng 7 2021
1.
Ta thấy: $-1\leq \cos x\leq 1$
$\Leftrightarrow 1\leq 2\cos x+3\leq 5$
$\Leftrightarrow 1\leq \sqrt{2\cos x+3}\leq \sqrt{5}$
$\Leftrightarrow -3\leq \sqrt{2\cos x+3}-4\leq \sqrt{5}-4$
Vậy $y_{\min}=-3$ khi $x=(2k+1)\pi$, $y_{\max}=\sqrt{5}-4$ khi $x=2k\pi$ với $k$ nguyên.
AH
Akai Haruma
Giáo viên
27 tháng 7 2021
2.
\(y=\cos ^2x-6\sin x+3=1-\sin ^2x-6\sin x+3\)
\(=-\sin ^2x-6\sin x+4\)
Ta thấy: $\sin ^2x\leq 1\Rightarrow -\sin ^2x\geq -1$
$\sin x\leq 1\Leftrightarrow -6\sin x\geq -6$
$\Rightarrow y=-\sin ^2x-6\sin x+4\geq -1-6+4=-3$
Vậy $y_{\min}=-3$. Giá trị này đạt tại $x=2k\pi +\frac{\pi}{2}$ với $k$ nguyên.
Mặt khác:
\(y=-\sin ^2x-6\sin x+4=9-(\sin x+1)(\sin x+5)\)
$-1\leq \sin x\leq 1\Rightarrow (\sin x+1)(\sin x+5)\geq 0$
$\Rightarrow y=9-(\sin x+1)(\sin x+5)\leq 9$
Vậy $y_{\max}=9$. Giá trị này đạt tại $x=2k\pi -\frac{\pi}{2}$ với $k$ nguyên.
HP
17 tháng 9 2021
1.1.
\(sinx=\dfrac{1}{4}\Leftrightarrow\left[{}\begin{matrix}x=arcsin\dfrac{1}{4}+k2\pi\\x=\pi-arcsin\dfrac{1}{4}+k2\pi\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 9 2021
Quy tắc b và c là phép biến hình (quy tắc b là phép đối xứng trục, quy tắc c là phép đối xứng tâm)
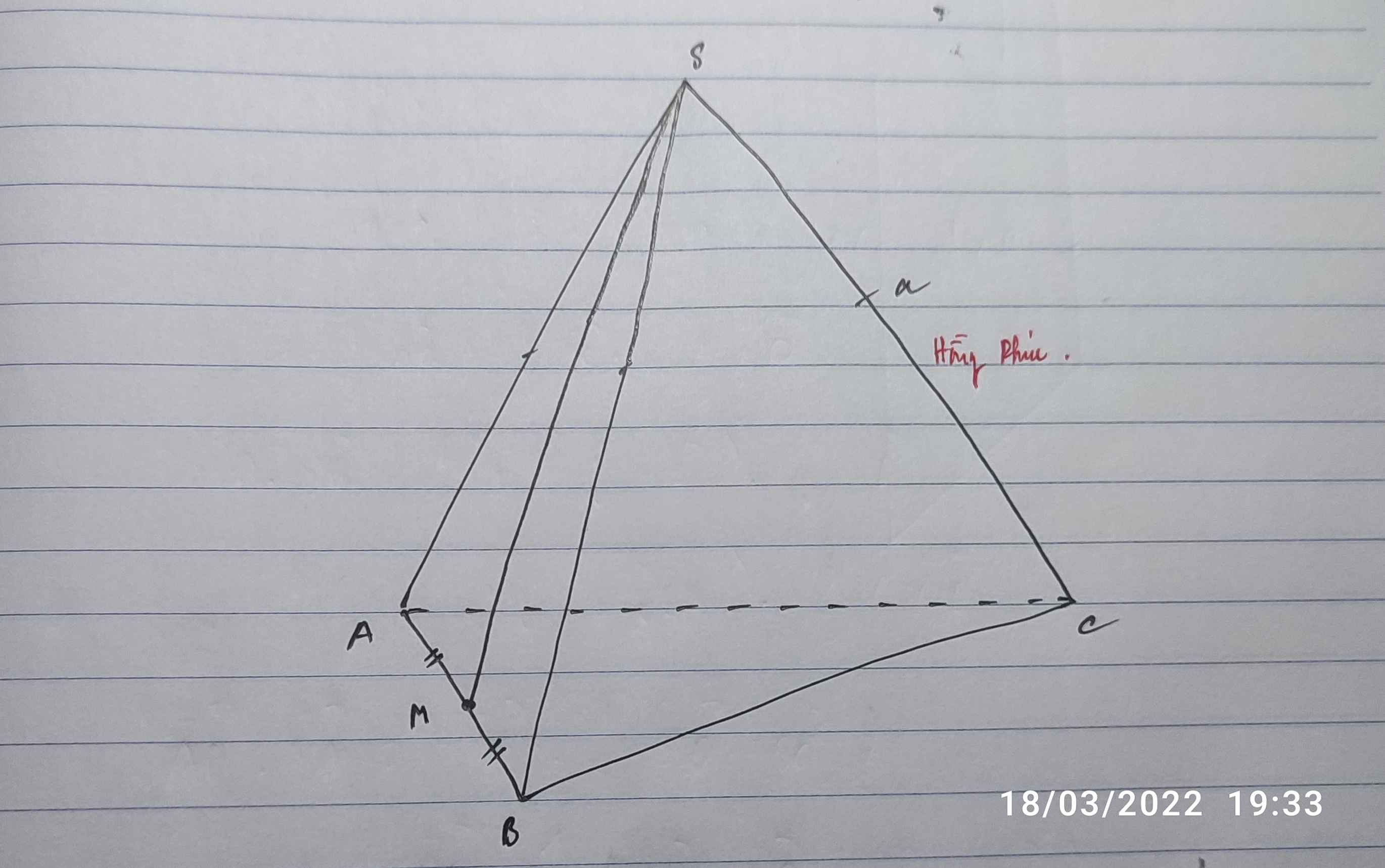
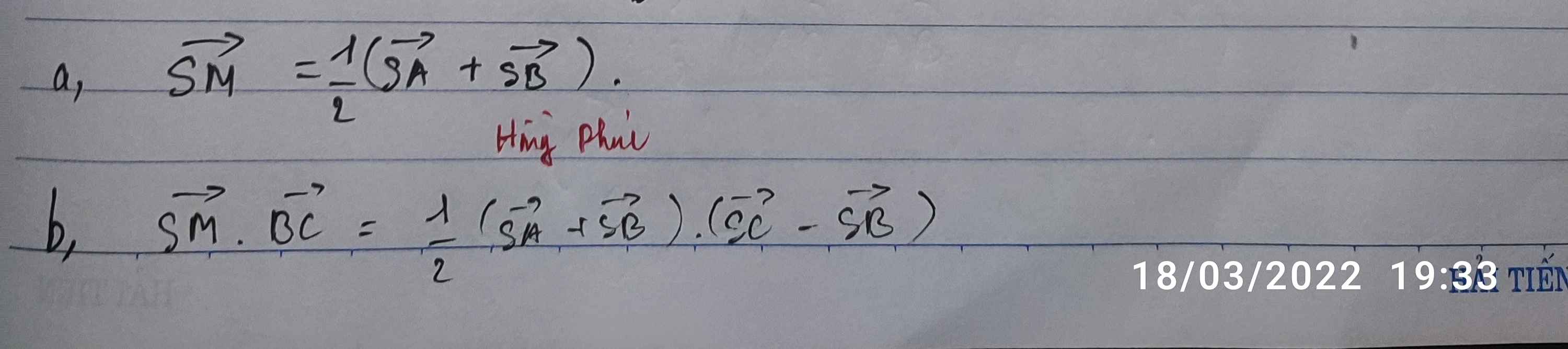
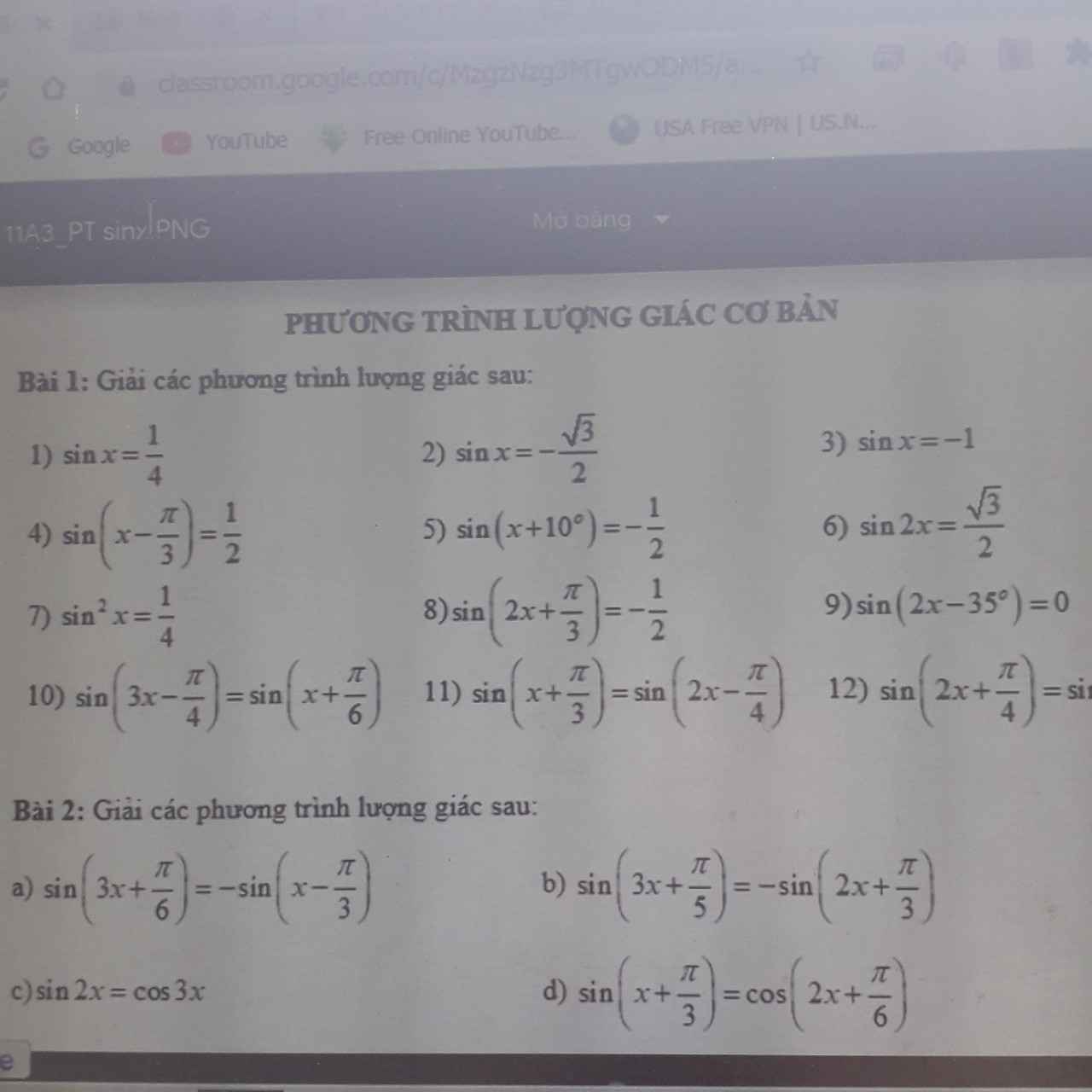
theo đề bài ta có \(n\ge4\)
\(C^2_2.C_{n-2}^2=2.C_{n-2}^4\Leftrightarrow\dfrac{\left(n-2\right)!}{2!\left(n-4\right)!}=\dfrac{2.\left(n-2\right)!}{4!.\left(n-6\right)!}\)
\(\Leftrightarrow6\left(n-2\right)\left(n-3\right)=\left(n-2\right)\left(n-3\right)\left(n-4\right)\left(n-5\right)\)
\(\Leftrightarrow6=n^2-9n+20\) \(\Leftrightarrow\left[{}\begin{matrix}n=2\left(\text{loại}\right)\\n=7\end{matrix}\right.\)
Vậy còn câu
này b có thể giúp mk đc ko