
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
\(\lim\limits_{x\to 2}\frac{x^2+ax+b}{2x^2-x-6}=\lim\limits_{x\to 2}\frac{x^2+ax+b}{(x-2)(2x+3)}\)
Để giới hạn này là hữu hạn thì $x^2+ax+b\vdots x-2$
$\Rightarrow 2^2+a.2+b=0\Leftrightarrow 2a+b=-4$
Đáp án A.
\(2x^2-x-6=0\) có 1 nghiệm \(x=2\)
Do đó giới hạn đã cho là hữu hạn khi và chỉ khi \(x^2+ax+b=0\) cũng có 1 nghiệm \(x=2\)
\(\Rightarrow4+2a+b=0\Rightarrow b=-2a-4\)
Vậy:
\(\lim\limits_{x\rightarrow2}\dfrac{x^2+ax-2a-4}{2x^2-x-6}=\lim\limits_{x\rightarrow2}\dfrac{\left(x-2\right)\left(x+2\right)+a\left(x-2\right)}{\left(x-2\right)\left(2x+3\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{\left(x-2\right)\left(x+a+2\right)}{\left(x-2\right)\left(2x+3\right)}=\lim\limits_{x\rightarrow2}\dfrac{x+a+2}{2x+3}=\dfrac{a+4}{7}\)
\(\Rightarrow\dfrac{a+4}{7}=\dfrac{3}{2}\Rightarrow a=\dfrac{13}{2}\Rightarrow b=-2a-4=-17\)
\(\Rightarrow2a+b=-4\)


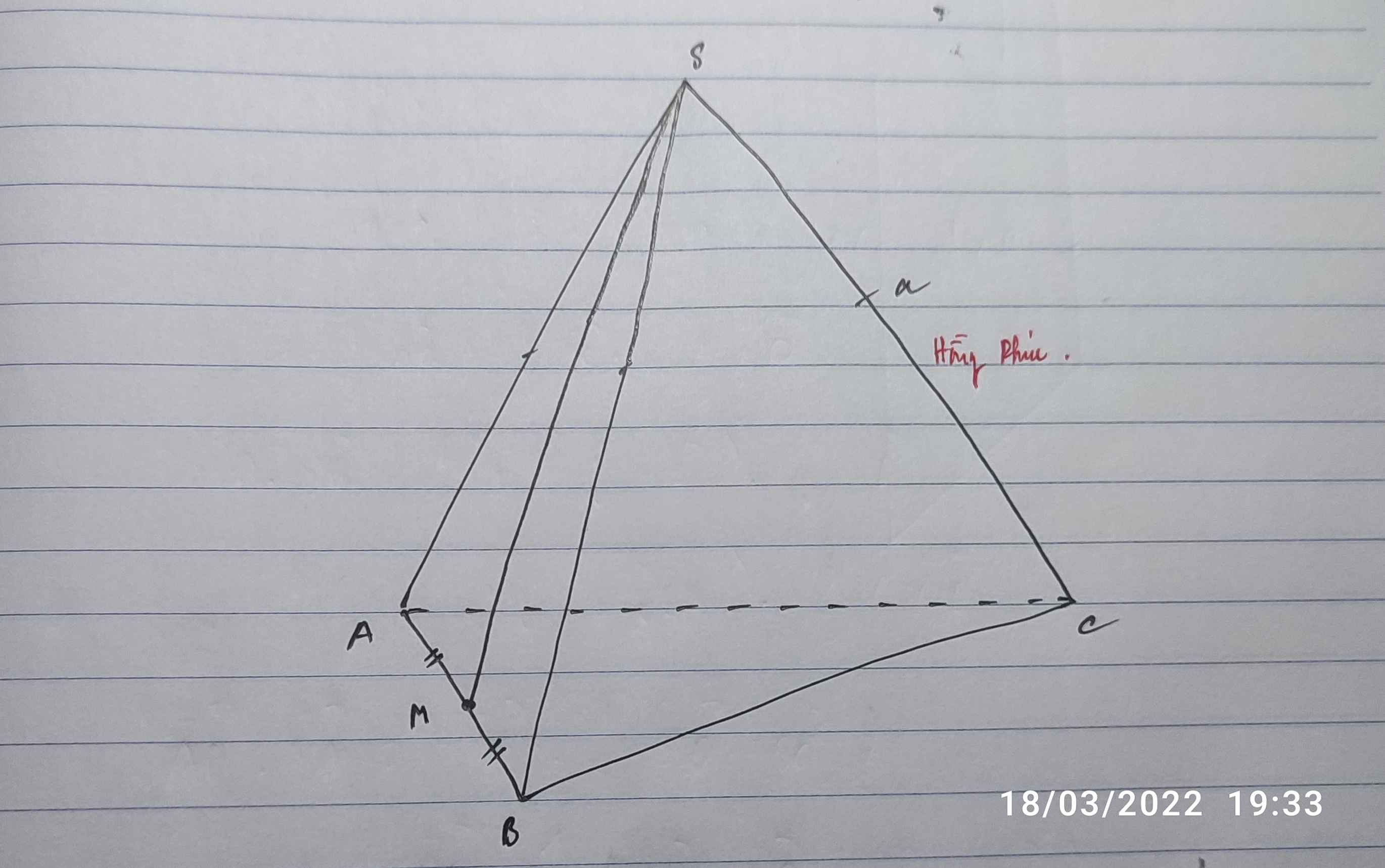
Do MN là đường trung bình tam giác ABC \(\Rightarrow MN||AB\) mà \(AB||CD\Rightarrow MN||CD\)
MN và (ABCD) không có điểm chung \(\Rightarrow MN||\left(ABCD\right)\)
MN và (SCD) không có điểm chung \(\Rightarrow MN||\left(SCD\right)\)
MN nằm trên (SAB) nên MN không song song (SAB)
Vậy MN song song với cả (ABCD) và (SCD)

Khoảng cách từ M để ABC bằng MA
Khoảng cách từ EF đến SAB bằng EM = AF


TH1: Xét cox = 0 ( có p là nghiệm ko)
TH2: Xét \(\cos x\ne0\). Ta chia cả hai vế \(\cos^2x\)
Pt trở thành \(2\tan^2x-4\tan x+4-1\left(1+\tan^2x\right)=0\)
\(\Leftrightarrow\tan^2x-4\tan x+3=0\)
Đặt \(\tan x=t\). Giải pt nữa là xg ạ
\(2sin^2x-4sinx.cosx+4cos^2x=1\)
\(\Leftrightarrow2\left(sin^2x+cos^2x\right)-4sinx.cosx+2cos^2x-1=0\)
\(\Leftrightarrow2-2sin2x+cos2x=0\)
\(\Leftrightarrow2sin2x-cos2x=2\)
\(\Leftrightarrow\sqrt{5}\left(\dfrac{2}{\sqrt{5}}sin2x-\dfrac{1}{\sqrt{5}}cos2x\right)=2\)
\(\Leftrightarrow sin\left(2x-arccos\dfrac{2}{\sqrt{5}}\right)=\dfrac{2}{\sqrt{5}}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-arccos\dfrac{2}{\sqrt{5}}=arcsin\dfrac{2}{\sqrt{5}}+k2\pi\\2x-arccos\dfrac{2}{\sqrt{5}}=\pi-arcsin\dfrac{2}{\sqrt{5}}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}arccos\dfrac{2}{\sqrt{5}}+\dfrac{1}{2}arcsin\dfrac{2}{\sqrt{5}}+k\pi\\x=\dfrac{\pi}{2}+\dfrac{1}{2}arccos\dfrac{2}{\sqrt{5}}-\dfrac{1}{2}arcsin\dfrac{2}{\sqrt{5}}+k\pi\end{matrix}\right.\)









1.
Ta thấy: $-1\leq \cos x\leq 1$
$\Leftrightarrow 1\leq 2\cos x+3\leq 5$
$\Leftrightarrow 1\leq \sqrt{2\cos x+3}\leq \sqrt{5}$
$\Leftrightarrow -3\leq \sqrt{2\cos x+3}-4\leq \sqrt{5}-4$
Vậy $y_{\min}=-3$ khi $x=(2k+1)\pi$, $y_{\max}=\sqrt{5}-4$ khi $x=2k\pi$ với $k$ nguyên.
2.
\(y=\cos ^2x-6\sin x+3=1-\sin ^2x-6\sin x+3\)
\(=-\sin ^2x-6\sin x+4\)
Ta thấy: $\sin ^2x\leq 1\Rightarrow -\sin ^2x\geq -1$
$\sin x\leq 1\Leftrightarrow -6\sin x\geq -6$
$\Rightarrow y=-\sin ^2x-6\sin x+4\geq -1-6+4=-3$
Vậy $y_{\min}=-3$. Giá trị này đạt tại $x=2k\pi +\frac{\pi}{2}$ với $k$ nguyên.
Mặt khác:
\(y=-\sin ^2x-6\sin x+4=9-(\sin x+1)(\sin x+5)\)
$-1\leq \sin x\leq 1\Rightarrow (\sin x+1)(\sin x+5)\geq 0$
$\Rightarrow y=9-(\sin x+1)(\sin x+5)\leq 9$
Vậy $y_{\max}=9$. Giá trị này đạt tại $x=2k\pi -\frac{\pi}{2}$ với $k$ nguyên.