K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
23 tháng 7 2021
Ta có \(P=\sum\dfrac{1}{\sqrt{2a^2+5ab+2b^2}}\le\sum\dfrac{1}{\sqrt{9ab}}=\dfrac{1}{3}\sum\dfrac{1}{\sqrt{ab}}\le\dfrac{1}{6}\sum\left(\dfrac{1}{a}+\dfrac{1}{b}\right)=\dfrac{1}{3}\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)=\dfrac{2}{3}\).
Dấu "=" xảy ra khi và chỉ khi \(a=b=c=\dfrac{3}{2}\)
XO
3 tháng 10 2020
Ta có : \(\hept{\begin{cases}\left|x^2+x-2\right|\ge0\forall x\\\left|x^2-1\right|\ge0\forall x\end{cases}}\Rightarrow\left|x^2+x-2\right|+\left|x^2-1\right|\ge0\forall x\)
Đẳng thức |x2 + x - 2| + |x2 - 1| = 0 xảy ra
<=> \(\hept{\begin{cases}x^2+x-2=0\\x^2-1=0\end{cases}}\Rightarrow\hept{\begin{cases}x^2+2x-x-2=0\\x^2=1\end{cases}}\Rightarrow\hept{\begin{cases}\left(x+2\right)\left(x-1\right)=0\\x^2=1\end{cases}}\)
+) Nếu : (x + 2)(x - 1) = 0
=> \(\orbr{\begin{cases}x+2=0\\x-1=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=-2\\x=1\end{cases}}\)
+) Nếu x2 = 1
=> \(\orbr{\begin{cases}x=1\\x=-1\end{cases}}\)
Vậy x = 1
V
3
2 tháng 7 2017
=(2^2-1)*(2^2+1)*(2^4+1)*...*(2^64+1)
=(2^4-1)(2^2+1)*(2^4+1)*...*(2^64+1)
=(2^8-1)(2^8+1)*...*(2^64+1)
=...
=(2^64-1)(2^64+1)
=2^128-1
mk vua lm ra do!!!!!!
NV
2
PN
13 tháng 8 2020
Ta giả sử \(4\) và \(\sqrt{7}\) (*) là \(a\) và \(b\left(a,b>0\right)\) thì ta có điều hiển nhiên sau : \(a+b>a-b\)
Đặt căn ở hai bên ta được : \(\sqrt{a+b}>\sqrt{a-b}\)
Thế (*) vào ta được : \(\sqrt{4+\sqrt{7}}>\sqrt{4-\sqrt{7}}\)
Do VT > VP nên trừ ở VP đi một số thực dương sẽ không đổi chiều dấu
Nên ta suy ra được \(\sqrt{4+\sqrt{7}}>\sqrt{4-\sqrt{7}}-\sqrt{2}\)
Hay viết cách khá là \(A>B\)
TA
13 tháng 8 2020
A=Căn ( 4 + căn 7) ...... B= Căn ( 4 - Căn 7 ) - Căn 2
xét:
Nếu A < B
Thì Căn (4 + căn 7) > Căn (4 - Căn7) - Căn 2
Nếu Căn (4+ căn 7) = 0
Thì Căn (4+Căn7) - Căn 2 = 0
Mà B= Căn (4 - Căn 7) ( Tức nhỏ hơn Căn (4 + căn 7)
=> A > B
Q
1
16 tháng 12 2019
\(ĐK:x\ge1\)
\(PT\Leftrightarrow x+3-4\sqrt{x+3}+4+\sqrt{x-1}=0\)
\(\Leftrightarrow\left(\sqrt{x+3}-2\right)^2+\sqrt{x-1}=0\)
\(\Leftrightarrow\hept{\begin{cases}\sqrt{x+3}=2\\x-1=0\end{cases}\Leftrightarrow}x=1\left(tm\right)\)
DH
1
MN
1 tháng 2 2020
HPT : \(\hept{\begin{cases}\frac{1}{x}+\frac{1}{y}=\frac{5}{36}\\\frac{4}{x}+\frac{3}{y}=\frac{1}{2}\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\frac{3}{x}+\frac{3}{y}=\frac{5}{12}\left(1\right)\\\frac{4}{x}+\frac{3}{y}=\frac{1}{2}\left(2\right)\end{cases}}\)
Từ (1) và (2), lấy vế trừ vế ta được :
\(\Leftrightarrow\left(\frac{4}{x}+\frac{3}{y}\right)-\left(\frac{3}{x}+\frac{3}{y}\right)=\frac{1}{2}-\frac{5}{12}\)
\(\Leftrightarrow\frac{1}{x}=\frac{1}{12}\)
\(\Leftrightarrow\frac{1}{y}=\frac{5}{36}-\frac{1}{x}=\frac{5}{36}-\frac{1}{12}=\frac{1}{18}\)
\(\Leftrightarrow\hept{\begin{cases}x=12\\y=18\end{cases}}\)
19 tháng 8 2021
a: \(A=\sqrt{64a^2}+2a=8a+2a=10a\)
b: \(B=3\sqrt{9a^6}-6a^3=3\cdot3a^3-6a^3=3a^3\)
19 tháng 8 2021
a) \(A=\sqrt{64a^2}+2a=8\left|a\right|+2a\)
b) \(B=3\sqrt{9a^6}-6a^3=9\left|a^3\right|-6a^3\)
17 tháng 10 2021
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=4\sqrt{41}\left(cm\right)\\AC=5\sqrt{41}\left(cm\right)\end{matrix}\right.\)
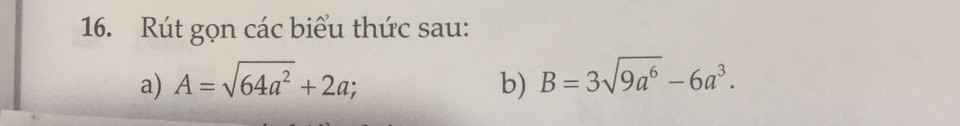
\(3x^2-2\left(m-3\right)x-2m+3=0\)
\(\Delta'=\left(m-3\right)^2-\left(-2m+3\right)=m^2-4m+6=\left(m-2\right)^2+2>0\)
\(\Rightarrow\) PT luôn có 2 nghiệm phân biệt
Áp dụng hệ thức Vi-et ta có: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-3\right)\\x_1x_2=-2m+3\end{matrix}\right.\)
Khi đó ta có:
\(P=x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2\\ =4\left(m-3\right)^2-2\left(-2m+3\right)=4m^2-20m+30\)
\(=\left(4m^2-20m+25\right)+5=\left(2m-5\right)^2+5\ge5\)
Dấu = xảy ra \(\Leftrightarrow2m-5=0\Leftrightarrow m=\dfrac{5}{2}\)
Ủa a=3 mà ạ