
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



7)Đk \(x\le2\)
Pt \(\Leftrightarrow x^2-x+8=4-2x\)
\(\Leftrightarrow x^2+x+4=0\)
\(\Delta=-15< 0\) => vô nghiệm
Vậy pt vô nghiệm
10) \(\sqrt{9x+9}-4\sqrt{\dfrac{x+1}{4}}=5\) (đk: \(x\ge-1\)
\(\Leftrightarrow\sqrt{\left(x+1\right).9}-\dfrac{4\sqrt{x+1}}{\sqrt{4}}=5\)
\(\Leftrightarrow3\sqrt{x+1}-2\sqrt{x+1}=5\)
\(\Leftrightarrow\sqrt{x+1}=5\) \(\Leftrightarrow x=24\) (tm)
Vậy \(S=\left\{24\right\}\)

c: \(\sqrt{3+\sqrt{8}}=\sqrt{2}+1\)
d: \(\sqrt{11+4\sqrt{6}}=2\sqrt{2}+3\)
e: \(\sqrt{14-6\sqrt{5}}=3-\sqrt{5}\)


a: \(\sqrt{2x+3}=5\)
\(\Leftrightarrow2x+3=25\)
hay x=11
b: \(\sqrt{\left(x-2\right)^2}=8\)
\(\Leftrightarrow\left|x-2\right|=8\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=8\\x-2=-8\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=10\\x=-6\end{matrix}\right.\)
a) \(\sqrt{3+2x}=5\left(đk:x\ge-\dfrac{3}{2}\right)\)
\(\Leftrightarrow3+2x=25\Leftrightarrow x=11\left(tm\right)\)
b) \(\sqrt{\left(x-2\right)^2}=8\)
\(\Leftrightarrow\left|x-2\right|=8\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=8\\x-2=-8\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=10\\x=-6\end{matrix}\right.\)
c) \(đk:x\le3\)
\(\Leftrightarrow\sqrt{3-x}-3\sqrt{3-x}+5\sqrt{3-x}=6\)
\(\Leftrightarrow3\sqrt{3-x}=6\)
\(\Leftrightarrow\sqrt{3-x}=2\Leftrightarrow3-x=4\Leftrightarrow x=-1\left(tm\right)\)
d) \(đk:x\ge0\)
\(\Leftrightarrow4\sqrt{x}-6\sqrt{x}+4\sqrt{x}=5\)
\(\Leftrightarrow2\sqrt{x}=5\Leftrightarrow\sqrt{x}=\dfrac{5}{2}\Leftrightarrow x=\dfrac{25}{4}\left(tm\right)\)
e) \(đk:x\ge-5\)
\(\Leftrightarrow2\sqrt{x+5}-3\sqrt{x+5}+4\sqrt{x+5}=6\)
\(\Leftrightarrow3\sqrt{x+5}=6\Leftrightarrow\sqrt{x+5}=2\Leftrightarrow x+5=4\Leftrightarrow x=-1\left(tm\right)\)
f) \(đk:x\ge-2\)
\(\Leftrightarrow3\sqrt{x+2}-5\sqrt{x+2}+4\sqrt{x+2}=6\)
\(\Leftrightarrow2\sqrt{x+2}=6\Leftrightarrow\sqrt{x+2}=3\Leftrightarrow x+2=9\Leftrightarrow x=7\left(tm\right)\)

1: Xét ΔABC vuông tại A có
\(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{C}=30^0\)
Xét ΔABC vuông tại A có
\(BC=\dfrac{AC}{\sin60^0}\)
\(=\dfrac{32\sqrt{3}}{3}\left(cm\right)\)
hay \(AB=\dfrac{16\sqrt{3}}{3}\left(cm\right)\)


b)\(\left\{{}\begin{matrix}x+y=-1+m\left(1\right)\\2x-y=2m\end{matrix}\right.\)
\(\Rightarrow3x=-1+3m\)
\(\Leftrightarrow x=\dfrac{-1+3m}{3}\)
Thay \(x=\dfrac{-1+3m}{3}\) vào (1) có:
\(\dfrac{-1+3m}{3}+y=-1+m\)\(\Leftrightarrow y=-1+m-\dfrac{-1+3m}{3}=-\dfrac{2}{3}\)
Suy ra với mọi m hệ luôn có nghiệm duy nhất \(\left(x;y\right)=\left(\dfrac{-1+3m}{3};-\dfrac{2}{3}\right)\)
\(xy=\left(\dfrac{-1+3m}{3}\right).\left(-\dfrac{2}{3}\right)=10\)
\(\Leftrightarrow m=-\dfrac{44}{3}\)
Vậy...
\(\left\{{}\begin{matrix}x+y=m-1\\2x-y=2m\end{matrix}\right.\)⇔\(\left\{{}\begin{matrix}2x+2y=2m-2\\2x-y=2m\end{matrix}\right.\)⇔\(\left\{{}\begin{matrix}3y=-2\\x=m-1-y\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}y=\dfrac{-2}{3}\\x=m-\dfrac{1}{3}\end{matrix}\right.\)
Ta có :
\(x.y=10\text{⇔}\left(m-\dfrac{1}{3}\right).\dfrac{-2}{3}=10\)
\(\text{⇔}m=\dfrac{-44}{3}\)


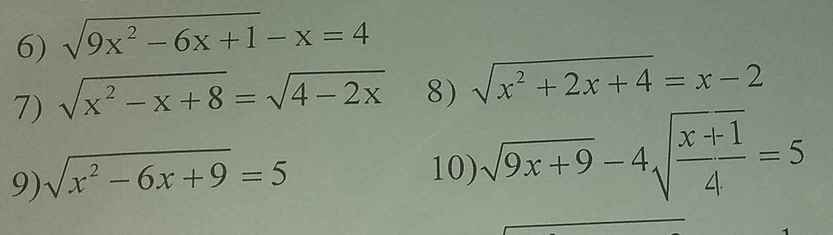
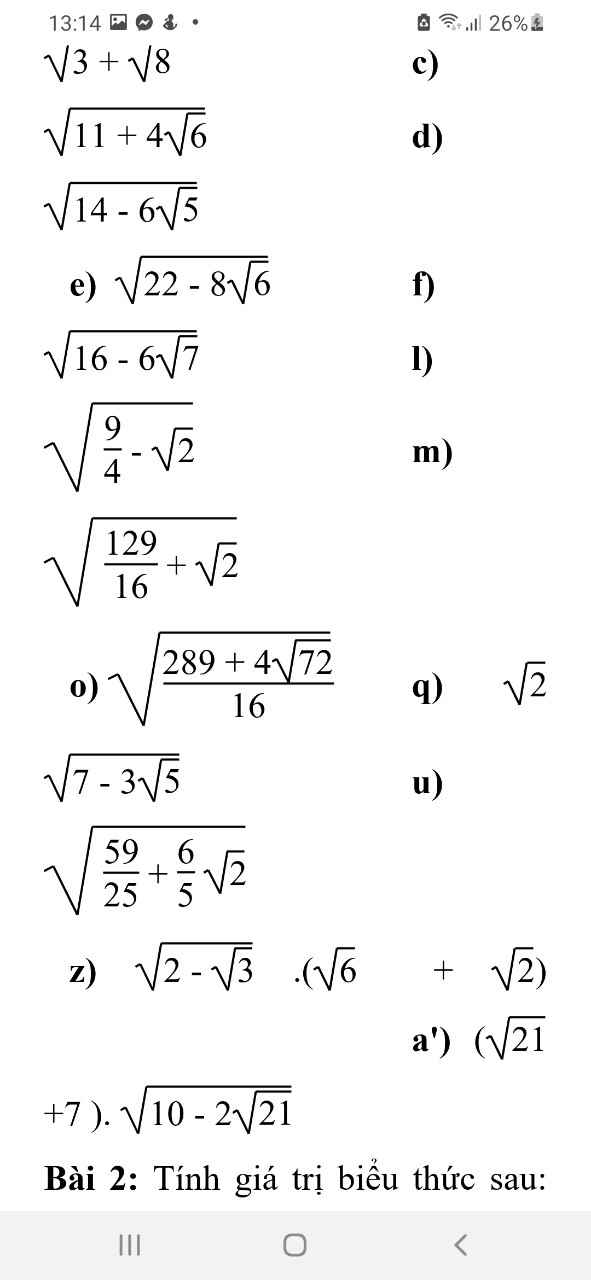







9: Ta có: \(\left(1+\sqrt{2}-\sqrt{3}\right)\left(1+\sqrt{2}+\sqrt{3}\right)\)
\(=\left(\sqrt{2}+1\right)^2-3\)
\(=3+2\sqrt{2}-3=2\sqrt{2}\)
10: Ta có: \(\dfrac{\sqrt{15}-\sqrt{5}}{\sqrt{6}-\sqrt{2}}+2\sqrt{10}\)
\(=\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{\sqrt{2}\left(\sqrt{3}-1\right)}+2\sqrt{10}\)
\(=\dfrac{\sqrt{10}}{2}+\dfrac{4\sqrt{10}}{2}=\dfrac{5\sqrt{10}}{2}\)
13)\(\dfrac{2\sqrt{10}+\sqrt{30}-2\sqrt{2}-\sqrt{6}}{2\sqrt{10}-2\sqrt{2}}=\dfrac{\sqrt{10}\left(2+\sqrt{3}\right)-\sqrt{2}\left(2+\sqrt{3}\right)}{2\left(\sqrt{10}-\sqrt{2}\right)}\)\(=\dfrac{\left(\sqrt{10}-\sqrt{2}\right)\left(2+\sqrt{3}\right)}{2\left(\sqrt{10}-\sqrt{2}\right)}=\dfrac{2+\sqrt{3}}{2}\)
14)sai đề? phải là \(\sqrt{3-\sqrt{5}}\)
\(=\dfrac{\sqrt{3-\sqrt{5}}\left(3+\sqrt{5}\right)}{2\sqrt{10}-2\sqrt{2}}=\dfrac{\sqrt{6-2\sqrt{5}}\left(3+\sqrt{5}\right)}{\sqrt{2}\left(2\sqrt{10}-2\sqrt{2}\right)}\)
\(=\dfrac{\sqrt{\left(\sqrt{5}-1\right)^2}\left(3+\sqrt{5}\right)}{4\left(\sqrt{5}-1\right)}=\dfrac{\left|\sqrt{5}-1\right|\left(3+\sqrt{5}\right)}{4\left(\sqrt{5}-1\right)}\)
\(=\dfrac{3+\sqrt{5}}{4}\)
15)\(\sqrt{\left(1-\sqrt{2016}\right)^2}.\sqrt{2017+2\sqrt{2016}}=\left|1-\sqrt{2016}\right|\sqrt{1+2\sqrt{2016}+2016}\)
\(=\left(\sqrt{2016}-1\right)\sqrt{\left(1+\sqrt{2016}\right)^2}=\left(\sqrt{2016}-1\right)\left(1+\sqrt{2016}\right)\)
\(=2015\)