
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tam giác AHC vuông tại H ( do AH \(⊥\)BC )
=> AH2 + CH2 = AC2 ( định lý Pytago )
=> 42 + CH2 = 52
=> 9 + CH2 = 25
=> CH2 = 16
=> CH = 4 cm ( CH > 0 )
Ta có: CH + BH = BC
=> 4 + BH = 9
=> BH = 5 cm
Tam giác AHC vuông tại H ( do AH\(⊥\)BC )
=> AH2 + CH2 = AC2 ( định lý Pytago )
=> 42 + CH2 = 52
=> 16 + CH2 = 25
=> CH2 = 9
=> CH = 3 cm ( CH > 0 )
Ta có: CH + BH = BC
=> 3 + BH = 9
=> BH = 6 cm
Tam giác ABH vuông tại H ( do AH\(⊥\)BC )
=> AH2 + BH2 = AB2 ( định lý Pytago )
=> 42 + 62 = AB2
=> 16 + 36 = AB2
=> AB2 = 52
=> AB = \(\sqrt{52}\)cm ( AB > 0 )
Xin lỗi bạn nhé, bài trên mình chưa để ý đề bài và làm sai, mình làm lại bài này, bạn vẫn dùng hình ở trên nha!
=> AB2 =

=>(2x-1)^2=24^2
=>2x-1=24 hoặc 2x-1=-24
=>x=-23/2 hoặc x=25/2

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=3^2+4^2=25\)
hay BC=5(cm)
b) Xét ΔABC có AB<AC<BC(3cm<4cm<5cm)
mà góc đối diện với cạnh AB là \(\widehat{ACB}\)
và góc đối diện với cạnh AC là \(\widehat{ABC}\)
và góc đối diện với cạnh BC là \(\widehat{BAC}\)
nên \(\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\)
Xét ΔABC có
HB là hình chiếu của AB trên BC
HC là hình chiếu của AC trên BC
AB<AC
Do đó: HB<HC
c) Xét ΔCAB vuông tại A và ΔCAD vuông tại A có
CA chung
AB=AD(gt)
Do đó: ΔCAB=ΔCAD(hai cạnh góc vuông)
Suy ra: CB=CD(hai cạnh tương ứng)
Xét ΔCBD có CB=CD(cmt)
nên ΔCBD cân tại C(Định nghĩa tam giác cân)

Bài 2 :
Bài 2 :
a, \(A=6x^3y^6z\)hệ số 6 ; biến x^3y^6z ; bậc 10
b, \(B=-\dfrac{2}{3}xy^2\left(9x^4y^2\right)=-6x^5y^4\)
hệ số -6 ; biến x^5y^4 ; bậc 9
Bài 3 :
\(A=3,5xy^2\) ta có \(x=\left|-2\right|=2;y=-1\)
Thay vào ta đc
A = 3,5 . 2 . 1 = 7

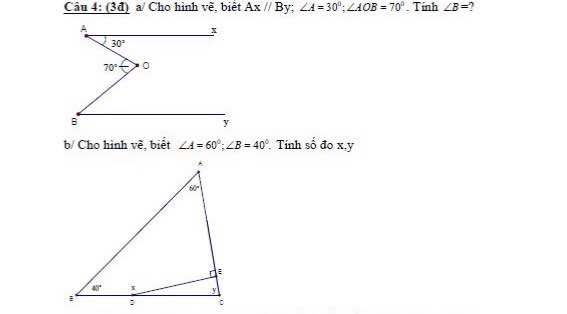


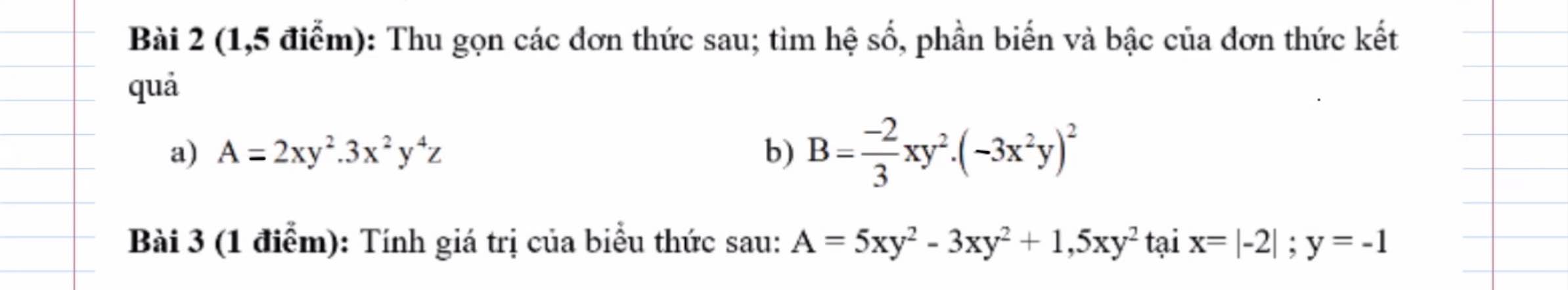
Câu 4a.
Kẻ tia $Om\parallel Ax$ như hình:
Vì $Ax\parallel Om$ nên $\widehat{AOm}=\widehat{xAO}=30^0$ (hai góc so le trong)
$\Rightarrow \widehat{mOB}=\widehat{AOB}-\widehat{AOm}=70^0-30^0=40^0$
$Ax\parallel By, Ax\parallel Om\Rightarrow By\parallel Om$
$\Rightarrow \widehat{B}=\widehat{mOB}=40^0$ (hai góc so le trong)
a) Trên nửa mặt phẳng bờ OB chứa điểm A, kẻ tia Oz//Ax//By
Ta có: Oz//Ax(cách vẽ)
\(\Rightarrow\widehat{xAO}=\widehat{AOz}=30^0\)( 2 góc so le trong)
Ta có: \(\widehat{AOz}+\widehat{zOB}=\widehat{AOB}\)
\(\Rightarrow\widehat{zOB}=\widehat{AOB}-\widehat{AOz}=70^0-30^0=40^0\)
Ta có: Oz//By
\(\Rightarrow\widehat{B}=\widehat{zOB}=40^0\)( 2 góc so le trong)
b) Xét tam giác ABC có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)( tổng 3 góc trong tam giác)
\(\Rightarrow\widehat{C}=180^0-\widehat{A}-\widehat{B}=180^0-60^0-40^0=80^0\)
\(\Rightarrow y=80^0\)
Xét tứ giác AEDB có:
\(\widehat{AED}+\widehat{EDB}+\widehat{ABD}+\widehat{BAE}=360^0\)
\(\Rightarrow\widehat{EDB}=360^0-\widehat{AED}-\widehat{ABD}-\widehat{BAE}=360^0-90^0-40^0-60^0=170^0\)
\(\Rightarrow x=170^0\)