K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 10 2021
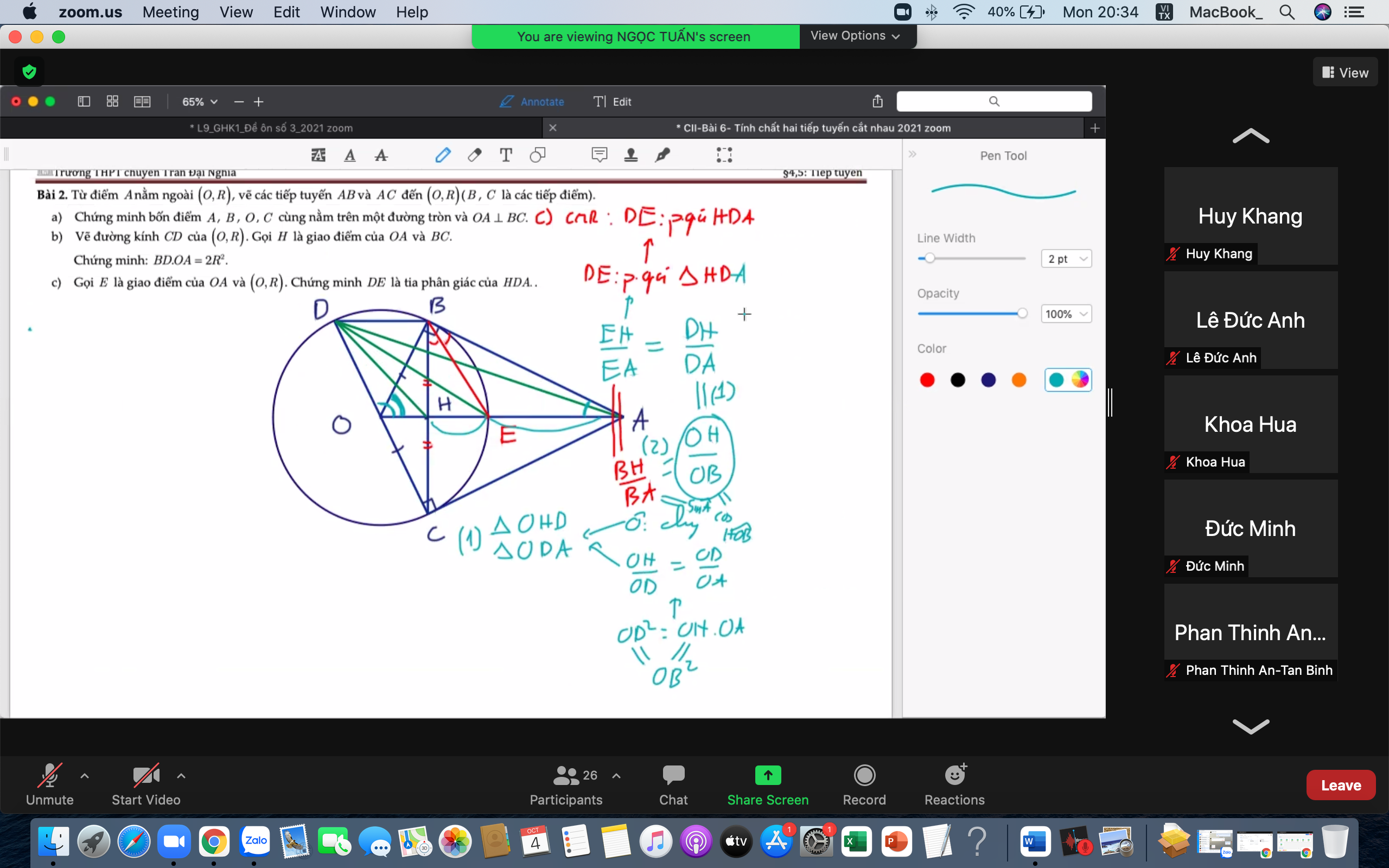
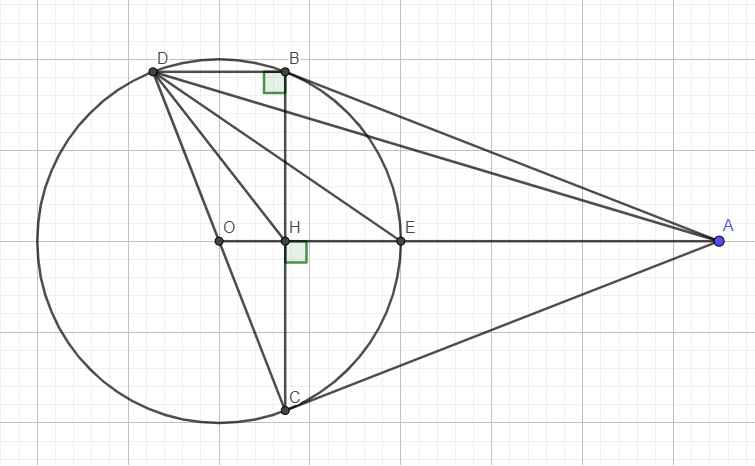
Ta có: \(\widehat{DBC}=90^0\) (nt chắn nửa đường tròn)
\(\Rightarrow BD||OA\) (cùng vuông góc BC)
\(\Rightarrow\widehat{BDE}=\widehat{DEO}\) (slt)
Mà \(\widehat{DEO}=\widehat{ODE}\) (OD=OE=R nên tam giác ODE cân tại O)
\(\Rightarrow\widehat{ODE}=\widehat{BDE}\) (1)
Lại có OH là đường trung bình tam giác BCD (đi qua 2 trung điểm)
\(\Rightarrow BD=2OH\)
Theo câu b: \(BD.OA=2R^2=2OD^2\Rightarrow2OH.OA=2OD^2\)
\(\Rightarrow\dfrac{OH}{OD}=\dfrac{OD}{OA}\)
Hai tam giác ODH và OAD có: \(\left\{{}\begin{matrix}\widehat{O}\text{ chung}\\\dfrac{OH}{OD}=\dfrac{OD}{OA}\end{matrix}\right.\)
\(\Rightarrow\Delta ODH\sim\Delta OAD\Rightarrow\widehat{ODH}=\widehat{OAD}\)
Mà \(\widehat{OAD}=\widehat{BDA}\) (so le trong) (2)
(1);(2) \(\Rightarrow\widehat{HDE}=\widehat{ADE}\) hay DE là phân giác \(\widehat{HDA}\)
PK
0
LG
2
20 tháng 9 2020
Ta có \(x^4+x^2+1=\left(x^2+1\right)^2-x^2=\left(x^2+x+1\right)\left(x^2-x+1\right)>0,\forall x\)
Mặt khác: \(x^2-3x+1=2\left(x^2-x+1\right)-\left(x^2+x+1\right)\)
Đặt \(y=\sqrt{\frac{x^2-x+1}{x^2+x+1}}\)(có thể viết điều kiện \(y\ge0\)hoặc chính xác hơn là \(\frac{\sqrt{3}}{3}\le y\le\sqrt{3}\)), ta được:
\(2y^2-1=\frac{-\sqrt{3}}{3}y=0\Leftrightarrow6y^2+\sqrt{3y}-3=0\), ta được \(y=\frac{\sqrt{3}}{3}\)(loại \(y=\frac{-\sqrt{3}}{2}\))
=> Phương trình có nghiệm là x=1
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 1 2022
Hàm bậc 2 có \(\left\{{}\begin{matrix}a=1>0\\-\dfrac{b}{2a}=6-m\end{matrix}\right.\) nên nghịch biến trên khoảng \(\left(-\infty;6-m\right)\)
Hàm nghịch biến trên khoảng đã cho khi:
\(6-m\ge2\Rightarrow m\le4\)
\(\Rightarrow\) Có 4 giá trị nguyên dương của m
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 4 2022
a.
\(0< a< \dfrac{\pi}{2}\Rightarrow cosa>0\Rightarrow cosa=\sqrt{1-sin^2a}=\dfrac{4}{5}\)
\(\Rightarrow tana=\dfrac{sina}{cosa}=\dfrac{3}{4}\) ; \(cota=\dfrac{1}{tana}=\dfrac{4}{3}\)
\(\Rightarrow A=\dfrac{\dfrac{4}{3}+\dfrac{3}{4}}{\dfrac{4}{3}-\dfrac{3}{4}}=...\)
b.
\(A=\dfrac{\dfrac{2sina}{cosa}+\dfrac{3cosa}{cosa}}{\dfrac{4sina}{cosa}-\dfrac{5cosa}{cosa}}=\dfrac{2tana+3}{4tana-5}=\dfrac{2.3+3}{4.3-5}=...\)
\(B=\dfrac{\dfrac{3sina}{cos^3a}-\dfrac{2cosa}{cos^3a}}{\dfrac{5sin^3a}{cos^3a}+\dfrac{4cos^3a}{cos^3a}}=\dfrac{3tana\left(1+tan^2a\right)-2\left(1+tan^2a\right)}{5tan^3a+4}=...\) em tự thay số
c.
\(B=\dfrac{cos^2x+2sinx.cosx+1}{sin^2x+3}=\dfrac{\dfrac{cos^2x}{cos^2x}+\dfrac{2sinx.cosx}{cos^2x}+\dfrac{1}{cos^2x}}{\dfrac{sin^2x}{cos^2x}+\dfrac{3}{cos^2x}}\)
\(=\dfrac{1+2tanx+\left(1+tan^2x\right)}{tan^2x+3\left(1+tan^2x\right)}=...\)
AH
Akai Haruma
Giáo viên
9 tháng 9 2021
Lời giải:
a.
$|x|\leq 2\Leftrightarrow -2\leq x\leq 2$
Tập $A=[-2;2]$
$(x-1)(x-4)< 0\Leftrightarrow 1< x< 4$
Tập $B=(1;4)$
Đến đây bạn có thể dễ dàng biểu diễn nó trên trục số
b.
$A\cap B=[-2;2]\cap (1;4)=(1;2]$
$A\cup B=[-2;2]\cup (1;4)=[-2;4)$
$A\setminus B= [-2;2]\setminus (1;4)=[-2;1]$
5 tháng 7 2021
- Xét : \(x^2+8x-20\le0\)
\(\Rightarrow-10\le x\le2\)
Mà \(x>0\)
\(\Rightarrow0< x\le2\)
- Xét \(x^2-2\left(m+3\right)x+m^2-2m< 0\)
Có : \(\Delta^,=b^{,2}-ac=\left(m+3\right)^2-\left(m^2-2m\right)\)
\(=m^2+6m+9-m^2+2m=8m+9\)
- Để bất phương trình có nghiệm
\(\Leftrightarrow\Delta>0\)
\(\Leftrightarrow m>-\dfrac{9}{8}\)
=> Bất phương trình có nghiệm \(S=\left(x_1;x_2\right)\)
Mà \(0< x\le2\)
\(\Rightarrow0< x_1< x_2\le2\)
\(TH1:x=2\)
\(\Rightarrow4-4\left(m+3\right)+m^2-2m< 0\)
\(\Rightarrow3-\sqrt{17}< m< 3+\sqrt{17}\)
\(TH2:0< x_1< x_2< 2\)
\(\Rightarrow\left\{{}\begin{matrix}m^2-2m>0\\m^2-6m-8>0\\0< 2\left(m+3\right)< 2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m< 0\\m>2\end{matrix}\right.\\\left[{}\begin{matrix}m>3+\sqrt{17}\\m< 3-\sqrt{17}\end{matrix}\right.\\-3< m< -2\end{matrix}\right.\)
Vậy \(3-\sqrt{7}< m< 3+\sqrt{7}\)
6 tháng 7 2021
Ban ơi :(( ngay chỗ dấu ngoặc nhọn đầu tiên của TH2 có công thức j k bạn?
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 7 2021
Nếu \(y\le0\Rightarrow\left(y-4\right)^2\ge16>9\left(ktm\right)\Rightarrow y>0\)
Nếu \(x\ge0\Rightarrow\left(x+5\right)^2\ge25>9\left(ktm\right)\Rightarrow x< 0\)
Đặt \(\left\{{}\begin{matrix}-x=a>0\\y=b>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left(a-5\right)^2+\left(b-4\right)^2\le9\\3a+b\ge14\end{matrix}\right.\)
Ta có:
\(14^2\le\left(3a+b\right)^2\le\left(3^2+1\right)\left(a^2+b^2\right)\Rightarrow a^2+b^2\ge\dfrac{196}{10}=\dfrac{98}{5}\)
\(P_{min}=\dfrac{98}{5}\) khi \(\left(a;b\right)=\left(\dfrac{21}{5};\dfrac{7}{5}\right)\) hay \(\left(x;y\right)=\left(-\dfrac{21}{5};\dfrac{7}{3}\right)\)
Lại có:
\(\left(a-5\right)^2+\left(b-4\right)^2\le9\Leftrightarrow a^2+b^2\le10a+8b-32\le\sqrt{\left(10^2+8^2\right)\left(a^2+b^2\right)}-32\)
\(\Rightarrow P\le2\sqrt{41}\sqrt{P}-32\Leftrightarrow P-2\sqrt{41}\sqrt{P}+32\le0\)
\(\Rightarrow\left(\sqrt{P}-3-\sqrt{41}\right)\left(\sqrt{P}-3+\sqrt{41}\right)\le0\) (1)
Do \(P\ge\dfrac{98}{5}\Rightarrow\sqrt{P}-3+\sqrt{41}>0\)
Nên (1) tương đương: \(\sqrt{P}-3-\sqrt{41}\le0\Rightarrow P\le50+6\sqrt{41}\)
\(P_{max}=50+6\sqrt{41}\) khi \(\left(a;b\right)=\left(5+\dfrac{15}{\sqrt{41}};4+\dfrac{12}{\sqrt{41}}\right)\)
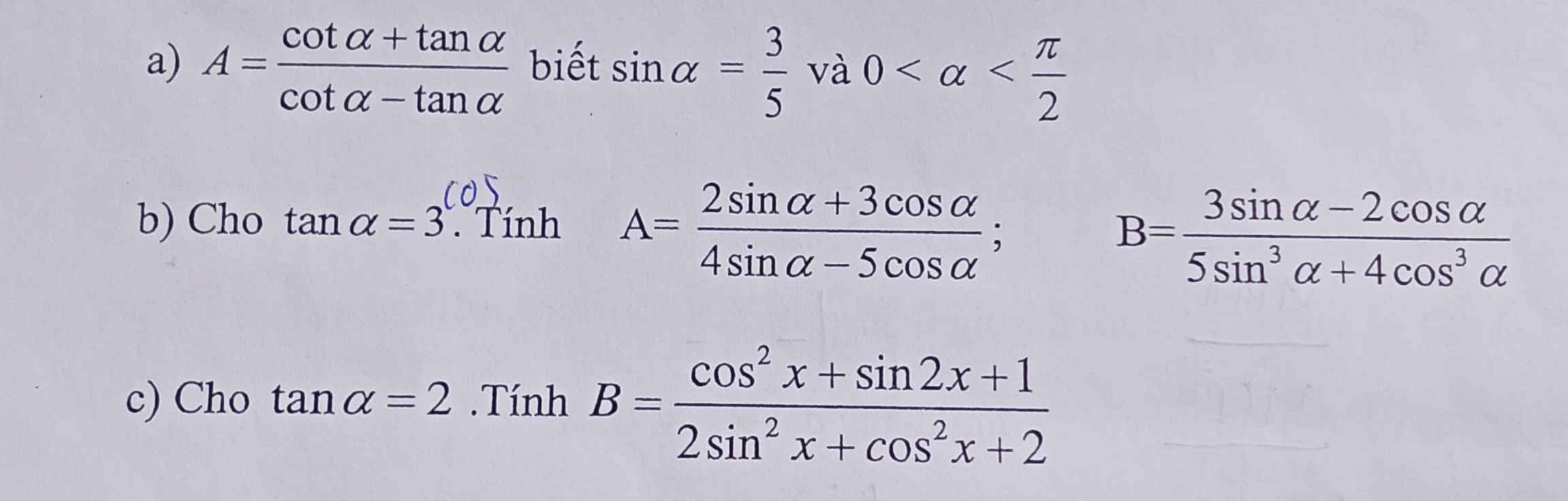
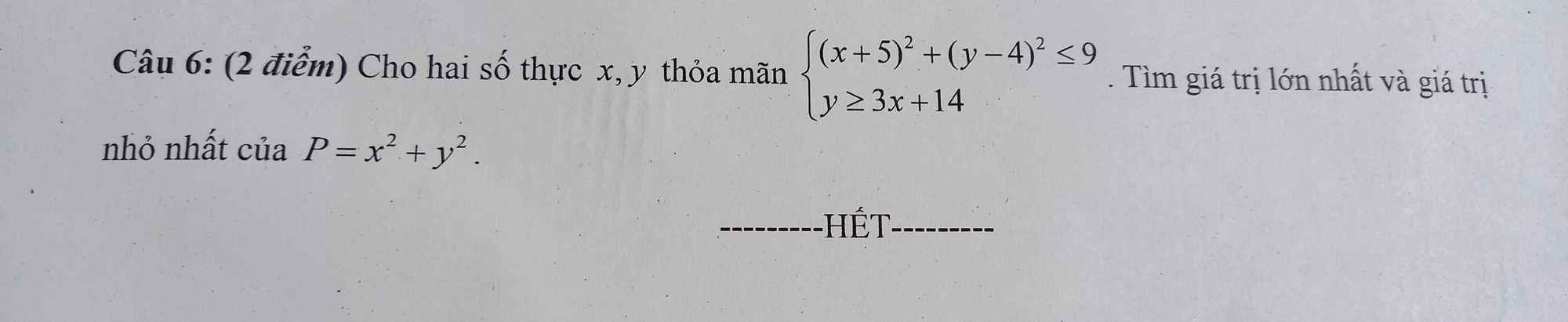
Bài 4:
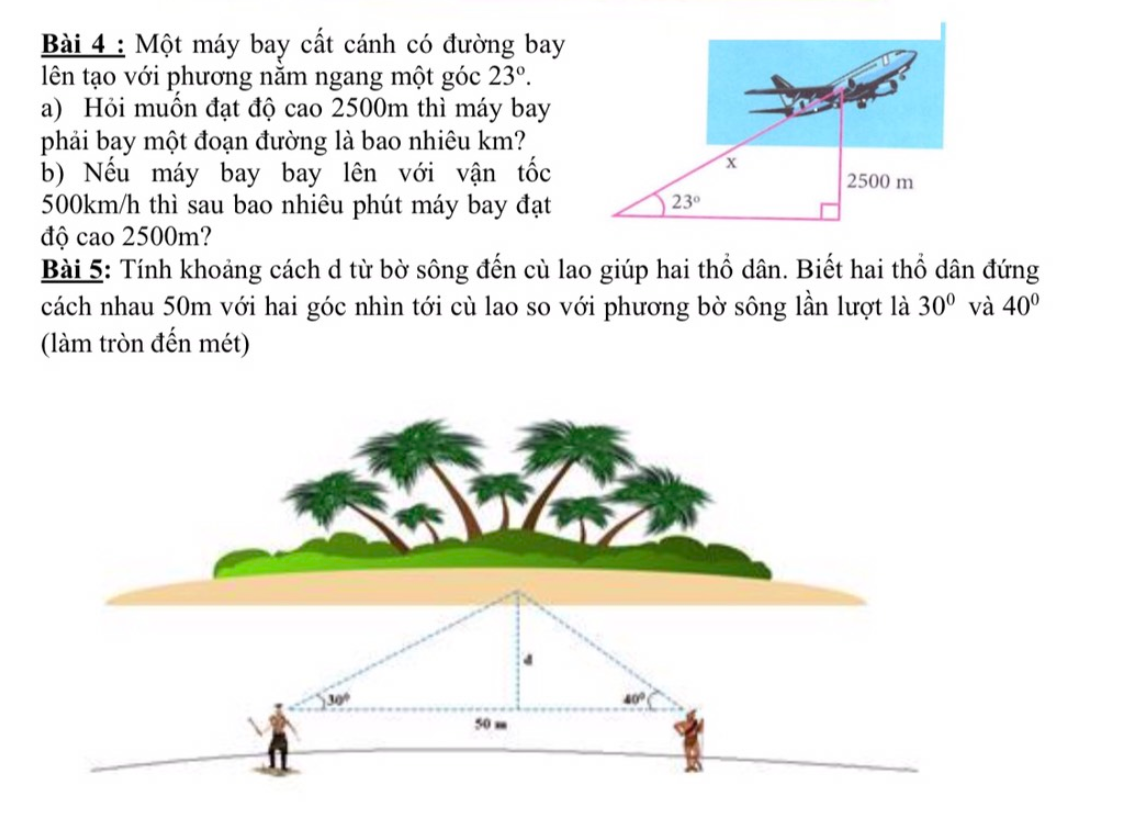
a) Gọi AB là độ cao máy bay, BC là đoạn đường máy bay bay
Áp dụng tslg trong tam giác ABC vuông tại A:
\(sinC=\dfrac{AB}{BC}\Rightarrow BC=\dfrac{AB}{sinC}=\dfrac{2500}{sin23^0}\approx6398\left(m\right)\)
b) Đổi: \(6398m=6,398km\)
Thời gian máy bay đạt độ cao 2500m:
\(t=\dfrac{S}{v}=\dfrac{6,398}{500}\approx0,03h=1,8ph\)
nốt bài 5 ik =))