Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(x^2+y^2-2x+4y+6=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\)
\(=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1>0\forall x,y\)
b) \(2x^2+2x+3=2\left(x^2+x+\dfrac{1}{4}\right)+\dfrac{5}{2}\)
\(=2\left(x+\dfrac{1}{2}\right)^2+\dfrac{5}{2}\ge\dfrac{5}{2}>0\forall x\)
c) \(x^2+y^2+z^2\ge xy+yz+xz\)
\(\Leftrightarrow2x^2+2y^2+2z^2\ge2xy+2yz+2xz\)
\(\Leftrightarrow\left(x^2-2xy+y^2\right)+\left(y^2+2yz+z^2\right)+\left(x^2+2xz+z^2\right)\ge0\)
\(\Leftrightarrow\left(x-y\right)^2+\left(y-z\right)^2+\left(x-z\right)^2\ge0\left(đúng\right)\)
\(ĐTXR\Leftrightarrow x=y=z\)

a, \(\left(2x+1\right)^2-2\left(2x+1\right)\left(x-3\right)+\left(x-3\right)^2\)
\(=\left(2x+1-x+3\right)^2=\left(x+4\right)^2\)
b, \(xy+xz+3y+3z=x\left(y+z\right)+3\left(y+z\right)=\left(x+3\right)\left(y+z\right)\)
c, \(xy-xz+y-z=x\left(y-z\right)+\left(y-z\right)=\left(x+1\right)\left(y-z\right)\)
d, \(x^2-xy-8x+8y=\left(x^2-xy\right)-\left(8x-8y\right)\)
\(=x\left(x-y\right)-8\left(x-y\right)=\left(x-8\right)\left(x-y\right)\)
e, \(x^2+2xy+y^2-xz-yz=\left(x^2+2xy+y^2\right)-\left(xz+yz\right)\)
\(=\left(x+y\right)^2-z\left(x+y\right)=\left(x+y+z\right)\left(x+y\right)\)
f, \(25-4x^2-4xy-y^2=25-\left(4x^2+4xy+y^2\right)\)
\(=5^2-\left(2x+y\right)^2=\left(5-2x-y\right)\left(5+2x+y\right)\)
1,
a, (2x + 1- x + 3)2 = (x+4)2
b,\(x\left(y+z\right)+3\left(y+z\right)=\left(y+z\right)\left(x+3\right)\)
c, \(x\left(y-z\right)+\left(y-z\right)=\left(y-z\right)\left(x+1\right)\)
d,\(x\left(x-y\right)+8\left(y-x\right)\)=\(\left(x-y\right)\left(x-8\right)\)
e,\(\left(x+y\right)^2-z\left(x+y\right)\)=\(\left(x+y\right)\left(x+y-z\right)\)
f,\(25-\left(4x^2+4xy+y^2\right)=5^2-\left(2x+y\right)^2\)
\(=\left(5+2x+y\right)\left(5-2x-y\right)\)
Chúc các bn hc tốt![]()

2:
a: \(=\left(2x^2-xy\right)+\left(2xz-yz\right)\)
\(=x\left(2x-y\right)+z\left(x-2y\right)=\left(x-2y\right)\left(x+z\right)\)
b: \(=\left(x^2-4y^2\right)-\left(x-2y\right)\)
\(=\left(x-2y\right)\left(x+2y\right)-\left(x-2y\right)\)
\(=\left(x-2y\right)\left(x+2y-1\right)\)
c: \(=\left(y^2+10y+25\right)-9z^2\)
\(=\left(y+5\right)^2-\left(3z\right)^2\)
\(=\left(y+5+3z\right)\left(y+5-3z\right)\)
d: \(=\left(x+2y\right)^3-\left(x-2y\right)\left(x+2y\right)\)
\(=\left(x+2y\right)\left[\left(x+2y\right)^2-\left(x-2y\right)\right]\)
\(=\left(x+2y\right)\left(x^2+4xy+4y^2-x+2y\right)\)
1:
a: \(x\left(3-4x\right)+5\left(3-4x\right)=\left(3-4x\right)\left(x+5\right)\)
b: \(2y\left(5y-6\right)-4\left(6-5y\right)\)
\(=2y\left(5y-6\right)+4\left(5y-6\right)\)
\(=2\left(5y-6\right)\left(y+2\right)\)
c: \(=27\left(x-2\right)^3-3x\left(x-2\right)^2\)
\(=3\left(x-2\right)^2\cdot\left[9\left(x-2\right)-x\right]\)
\(=3\left(x-2\right)^2\left(8x-18\right)=6\left(x-2\right)^2\cdot\left(4x-9\right)\)
d: \(=6y\left(x-y\right)\left(x+y\right)-8y\left(x+y\right)^2\)
\(=2y\left(x+y\right)\left[3\left(x-y\right)-4\left(x+y\right)\right]\)
\(=2y\left(x+y\right)\left(3x-3y-4x-4y\right)\)
\(=2y\left(x+y\right)\left(-x-7y\right)\)
Bài 1
a) x(3 - 4x) + 5(3 - 4x)
= (3 - 4x)(x + 5)
b) 2y(5y - 6) - 4(6- 5y)
= 2y(5y - 6) + 4(5y - 6)
= (5y - 6)(2y + 4)
= 2(5y - 6)(y + 2)
c) 27(x - 2)³ - 3x(2 - x)²
= 27(x - 2)³ - 3x(x - 2)²
= 3(x - 2)²[9(x - 2) - x]
= 3(x - 2)²(9x - 18 - x)
= 3(x - 2)²(8x - 18)
= 6(x - 2)²(4x - 9)
d) 6y(x² - y²) - 8y(x + y)²
= 6y(x - y)(x + y) - 8y(x + y)²
= 2y(x + y)[3(x - y) - 4(x + y)]
= 2y(x + y)(3x - 3y - 4x - 4y)
= 2y(x + y)(-x - 7y)
= -2y(x + y)(x + 7y)

Bài 2: a) Để tính giá trị của A = 5x(x^2-3) + x^2(7-5x) - 7x tại x = -3, ta thay x = -3 vào biểu thức và tính toán: A = 5(-3)((-3)^2-3) + (-3)^2(7-5(-3)) - 7(-3) = 5(-3)(9-3) + 9(7+15) + 21 = -15(6) + 9(22) + 21 = -90 + 198 + 21 = 129
Vậy giá trị của A tại x = -3 là 129.
Bài 3: a) Để rút gọn và tính giá trị của biểu thức c = 5x^2-3x(x+2), ta thay x = -3 vào biểu thức và tính toán: c = 5(-3)^2 - 3(-3)(-3+2) = 5(9) - 3(9)(-1) = 45 - 27 = 18
Vậy giá trị của c tại x = -3 là 18.
b) Để rút gọn và tính giá trị của biểu thức b = 3x^2y(2x^2-y) - 4x^2(4x^2-y^2), ta thay x = -3 và y = -2 vào biểu thức và tính toán: b = 3(-3)^2(-2)(2(-3)^2-(-2)) - 4(-3)^2(4(-3)^2-(-2)^2) = 3(9)(-2)(2(9)-2) - 4(9)(4(9)-4) = -54(18-2) - 36(36-4) = -54(16) - 36(32) = -864 - 1152 = -2016
Vậy giá trị của b tại x = -3 và y = -2 là -2016.
c) Để rút gọn và tính giá trị của biểu thức c = xy^2(x-xy) - x(x=y) + yx(2x^2-2xy), ta thay x = -3 và y = -2 vào biểu thức và tính toán: c = (-3)(-2)^2((-3)-(-3)(-2)) - (-3)(x=(-3)) + (-2)(-3)(2(-3)^2-2(-3)(-2)) = (-3)(4)(-3+6) - (-3)(x=(-3)) + (-2)(-3)(18-12) = (-3)(4)(3) - (-3)(x=(-3)) + (-2)(-3)(6) = (-12)(3) + (-3)(-3) + (-2)(-3)(6) = -36 + 9 + 36 = 9
Vậy giá trị của c tại x = -3 và y = -2 là 9.
2:
a: \(A=5x^3-15x+7x^2-5x^3-7x=7x^2-22x\)
Khi x=-3 thì A=7(-3)^2+22*3
=63+66
=129
b: \(B=x^4-x^2y^2+x^2y^2+y^4=x^4+y^4\)
Khi x=-3 và y=-2 thì B=(-3)^4+(-2)^4
=81+16
=97

\(1,=\left(x-2\right)\left(5-y\right)\\ 2,=2\left(x-y\right)^2-z\left(x-y\right)=\left(x-y\right)\left(2x-2y-z\right)\\ 3,=5xy\left(x-2y\right)\\ 4,=3\left(x^2-2xy+y^2-4z^2\right)=3\left[\left(x-y\right)^2-4z^2\right]\\ =3\left(x-y-2z\right)\left(x-y+2z\right)\\ 5,=\left(x+2y\right)^2-16=\left(x+2y-4\right)\left(x+2y+4\right)\\ 6,=-\left(6x^2-3x-4x+2\right)=-\left(2x-1\right)\left(3x-2\right)\\ 7,=\left(2x+y\right)\left(2x+y+x\right)=\left(2x+y\right)\left(3x+y\right)\\ 8,=\left(x-y\right)\left(x+5\right)\\ 9,=\left(x+1\right)^2-y^2=\left(x-y+1\right)\left(x+y+1\right)\\ 10,=\left(x^2-9\right)x=x\left(x-3\right)\left(x+3\right)\\ 11,=\left(x-2\right)\left(y+1\right)\\ 12,=\left(x-3\right)\left(x^2-4\right)=\left(x-3\right)\left(x-2\right)\left(x+2\right)\\ 13,=3\left(x+y\right)-\left(x+y\right)^2=\left(x+y\right)\left(3-x-y\right)\)
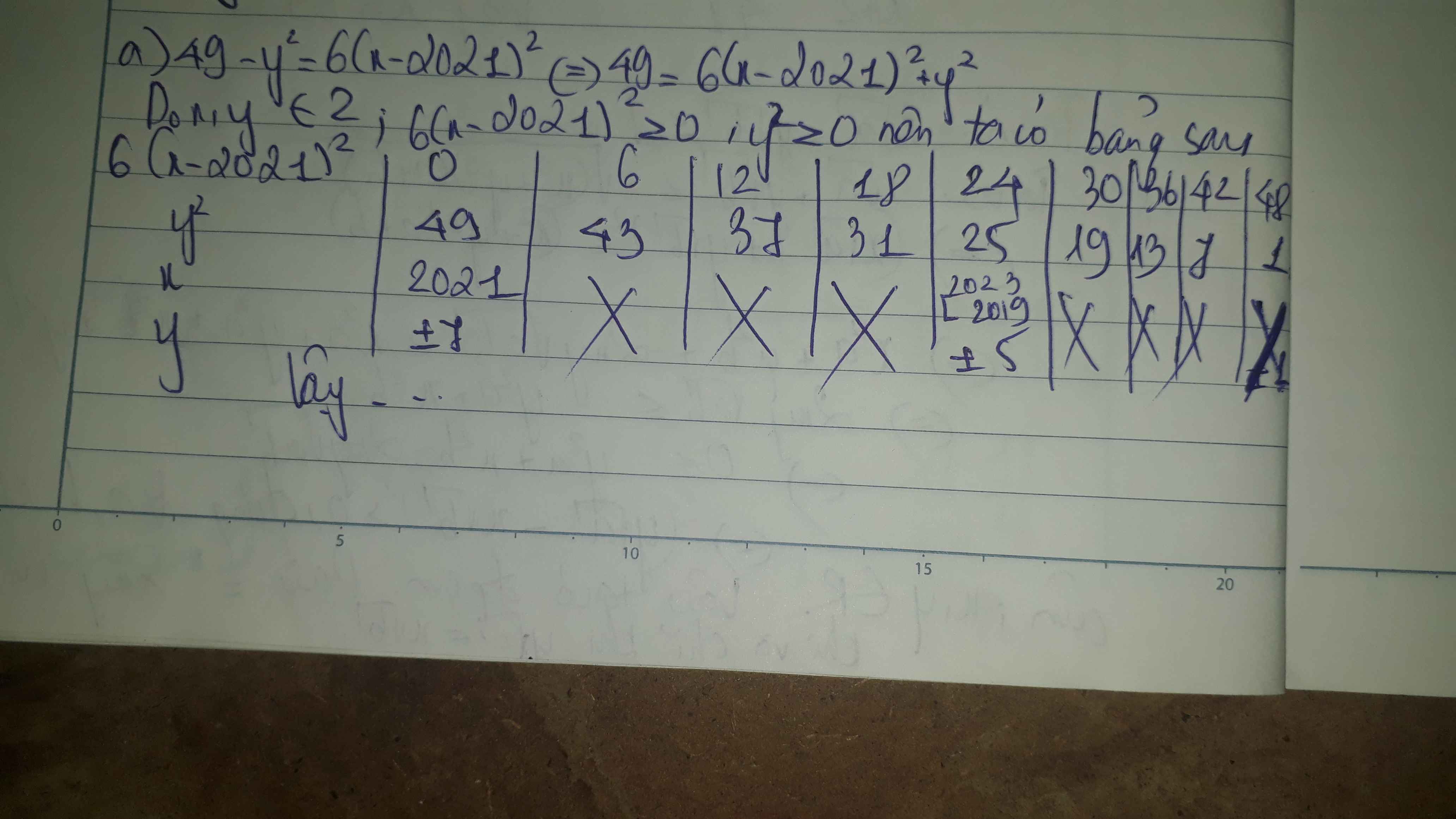
\(a,=\left(x+y\right)\left(y+z\right)\\ b,=x\left(x^2+2x+1\right)=x\left(x+1\right)^2\\ c,=\left(x-y\right)\left(x+y\right)+\left(x-y\right)=\left(x+y+1\right)\left(x-y\right)\\ d,= \left(2x-5\right)\left(2x+5\right)\\ e,=\left(4y-3\right)\left(4y+3\right)\)