
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
a) \(=\dfrac{\sqrt{5}.\sqrt{7}}{5}=\dfrac{\sqrt{35}}{5}\)
b) \(=\dfrac{\left|y\right|}{\sqrt{3}}=\dfrac{\sqrt{3}y}{3}\)
c) \(=\dfrac{\sqrt{2}}{\sqrt{t}}=\dfrac{\sqrt{2t}}{t}\)
d) \(=\sqrt{\dfrac{7p^2-3p^2}{7}}=\sqrt{\dfrac{4p^2}{7}}=\dfrac{2\left|p\right|}{\sqrt{7}}=\dfrac{-2\sqrt{7}p}{7}\)
Bài 2:
a) \(=\dfrac{\sqrt{21}-\sqrt{15}}{3}\)
b) \(=\dfrac{10\left(4+3\sqrt{2}\right)}{16-18}=-20-15\sqrt{2}\)
c) \(=\dfrac{\left(3\sqrt{10}-5\right)\left(6+\sqrt{10}\right)}{36-10}=\dfrac{18\sqrt{10}+30-30-5\sqrt{10}}{26}=\dfrac{13\sqrt{10}}{26}=\dfrac{\sqrt{10}}{2}\)

\(P=\dfrac{2\sqrt{x}+1+\left(1-\sqrt{x}\right)\left(1+\sqrt{x}\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}:\dfrac{\sqrt{x}+2}{\sqrt{x}}\)
\(=\dfrac{2\sqrt{x}+1+1-x}{\sqrt{x}\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}}{\sqrt{x}+2}=\dfrac{-x+2\sqrt{x}+2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)}=\dfrac{-x+2\sqrt{x}+2}{x+3\sqrt{x}+2}\)

ta có sinB=\(\dfrac{AH}{AB}\)\(\Rightarrow\)AH=AB.sinB=3,6.sin62=3,18
BH=\(\sqrt{AB^2-AH^2}\)(pytago)=\(\sqrt{3,6^2-3,18^2}\)=1,69
\(_{\widehat{C}}\)=90-\(\widehat{B}\)=90-62=28\(^0\)
sinC=\(\dfrac{AB}{BC}\)\(\Rightarrow\)BC=\(\dfrac{AB}{sinC}\)=\(\dfrac{3,6}{sin28}\)=7,67
mà:CH=BC-BH=7,67-1,69=5,98
AC=\(\sqrt{BC^2-AB^2}\)(pytago)=\(\sqrt{7,67^2-3,6^2}\)=6.77

a: Xét (O) có
CM là tiếp tuyến có M là tiếp điểm
CN là tiếp tuyến có N là tiếp điểm
Do đó: CM=CN
hay C nằm trên đường trung trực của MN(1)
Ta có: OM=ON
nên O nằm trên đường trung trực của MN(2)
Từ (1) và (2) suy ra OC là đường trung trực của MN

\(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=-1\end{matrix}\right.\)
8: \(=\dfrac{x_1^2+x_2^2}{\left(x_1\cdot x_2\right)^2}=\dfrac{2}{1}=2\)
9: \(=\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=2^3-3\cdot\left(-1\right)\cdot2=8+6=14\)
16: \(=\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}=\sqrt{2^2-4\cdot\left(-1\right)}=\sqrt{4+4}=2\sqrt{2}\)

a) Xét pt hoành độ gđ của (P) và (d) có:
\(\dfrac{1}{2}x^2=mx+2\) \(\Leftrightarrow x^2-2mx-4=0\) (1)
Có \(ac=1.\left(-4\right)< 0\)
=>Pt (1) luôn có hai nghiệm trái dấu
=> (P) và (d) luôn cắt nhau tại hai điểm phân biệt
b) \(M=\left(d\right)\cap Oy\Rightarrow M\left(0;2\right)\) \(\Rightarrow OM=2\)
Nhận xét: (P) luôn nằm phia trên trục hoành
(d) luôn cắt (P) tại hai điểm A(x1;y1) và B(x2;y2) với x1;x2 là hai nghiệm của pt (1) , x1.x2<0
=> A;B nằm khác phía nhau so với trục tung
Theo viet: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=-4\end{matrix}\right.\)
Do H và K lần lượt là hình chiếu của A và B trên trục hoành
=> \(OH=\left|x_1\right|\), \(OK=\left|x_2\right|\)
\(S_{MHK}=\dfrac{1}{2}.MO.HK=\dfrac{1}{2}.2\left(\left|x_1\right|+\left|x_2\right|\right)\)
\(\Leftrightarrow4=\left|x_1\right|+\left|x_2\right|\) \(\Leftrightarrow16=x_1^2+x_2^2+2\left|x_1x_2\right|\)
\(\Leftrightarrow16=\left(x_1+x_2\right)^2-2x_1x_2-2x_1x_2\) (do x1x2<0 => |x1x2|=-x1x2)
\(\Leftrightarrow16=4m^2-2\left(-4\right)-2\left(-4\right)\)
\(\Leftrightarrow m=0\)
Vậy...

\(\Delta=m^2-4\left(m-1\right)=m^2-4m+4=\left(m-2\right)^2\ge0\)
Để pt có 2 nghiệm pb khi x khác 2
Theo Vi et \(\left\{{}\begin{matrix}x_1+x_2=m\left(1\right)\\x_1x_2=m-1\left(2\right)\end{matrix}\right.\)
Vì x1 là nghiệm pt trên nên \(x_1^2=mx_1-m+1\)
Thay vào ta được \(mx_1-m+1+3x_2=19\)(3)
Từ (1) ; (3) ta có hệ \(\left\{{}\begin{matrix}mx_1+mx_2=m^2\\mx_1+3x_2=m+18\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(m-3\right)x_2=m^2-m-18\\x_2=m-x_1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{m^2-m-18}{m-3}\\x_1=\dfrac{m^2-3m-m^2+m+18}{m-3}=\dfrac{-2m+18}{m-3}\end{matrix}\right.\)
Thay vào (2) ta được \(\dfrac{\left(m^2-m-18\right)\left(-2m+18\right)}{\left(m-3\right)^2}=m-1\Rightarrow m=5;m=-3\)
bạn giải chi tiết xem còn nghiệm nào ko nhé


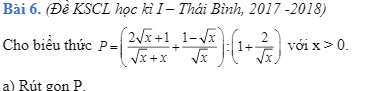


 Mình đang cần rất gấp từ câu 7 đến câu 21. Mọi người giải giúp mình. Mình cảm ơn !
Mình đang cần rất gấp từ câu 7 đến câu 21. Mọi người giải giúp mình. Mình cảm ơn !
 Giúp mình câu Viest với, mình phân tích không ra, mình đang cần gấp.Cảm ơn rất nhiều!
Giúp mình câu Viest với, mình phân tích không ra, mình đang cần gấp.Cảm ơn rất nhiều!
a: \(A=\sqrt{x^2+2x+5}=\sqrt{x^2+2x+1+4}\)
=>\(A=\sqrt{\left(x+1\right)^2+4}>=\sqrt{4}=2\)
b: \(B=\sqrt{x^2-4x+4+1}=\sqrt{\left(x-2\right)^2+1}>=1\)