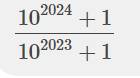Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Phân số này nên để ở dạng này thôi. Đây cũng là dạng khá rút gọn rồi. Không nên tính ra số cụ thể nhé bạn.

`7,`
`a, B+A=4x-2x^2+3`
`-> B=(4x-2x^2+3)-A`
`-> B=(4x-2x^2+3)-(x^2-2x+1)`
`B=4x-2x^2+3-x^2+2x-1`
`B=(-2x^2-x^2)+(4x+2x)+(3-1)`
`B=-3x^2+6x+2`
`b, C-A=-x+7`
`-> C=(-x+7)+A`
`-> C=(-x+7)+(x^2-2x+1)`
`-> C=-x+7+x^2-2x+1`
`C=x^2+(-x-2x)+(7+1)`
`C=x^2-3x+8`
`c,`
`A-D=x^2-2`
`-> D= A- (x^2-2)`
`-> D=(x^2-2x+1)-(x^2-2)`
`D=x^2-2x+1-x^2+2`
`D=(x^2-x^2)-2x+(1+2)`
`D=-2x+3`
`6,`
`a,`
`P+Q=4x-2x^2+3`
`-> Q=(4x-2x^2+3)-P`
`-> Q=(4x-2x^2+3)-(3x^2+x-1)`
`Q=4x-2x^2+3-3x^2-x+1`
`Q=(-2x^2-3x^2)+(4x-x)+(3+1)`
`Q=x^2+3x+4`
`b,`
`x^2-5x+2-P=H`
`-> H= (x^2-5x+2)-(3x^2+x-1)`
`H=x^2-5x+2-3x^2-x+1`
`H=(x^2-3x^2)+(-5x-x)+(2+1)`
`H=-4x^2-6x+3`
`c,`
`P-R=5x^2-3x-4`
`-> R= P- (5x^2-3x-4)`
`-> R=(3x^2+x-1)-(5x^2-3x-4)`
`R=3x^2+x-1-5x^2+3x+4`
`R=(3x^2-5x^2)+(x+3x)+(-1+4)`
`R=-2x^2+4x+3`

\(\frac{16}{81}=\left(\frac{4}{9}\right)^2=\left(-\frac{4}{9}\right)^2=\left(\frac{2}{3}\right)^2=\left(-\frac{2}{3}\right)^2\)

\(\frac{1}{12}-\left(-\frac{1}{6}-\frac{1}{4}\right)\)
\(=\frac{1}{12}-\left(-\frac{2}{12}-\frac{3}{12}\right)\)
\(=\frac{1}{12}+\frac{2}{12}+\frac{3}{12}\)
\(=\frac{1}{2}\)
Thanks bạn cute Jeon Koo Koo nhìu nha , tớ cảm ơn pạn rất nhìu :3

Hình bạn tự vẽ.
Bài 1.
a) Xét tam giác AHB và AHC có:
$\widehat{AHB}=\widehat{AHC}=90^o$ (gt)
$AB=AC$ (tam giác ABC cân tại A)
$AH$ chung.
Vậy $\Delta AHB=\Delta AHC$ (cạnh huyền - cạnh góc vuông)
\(\Rightarrow HB=HC\) (1)
b) Ta có: \(AC\bot AB;MB\bot AB\Rightarrow\) MB// AC $(2)$ do đó $\widehat{ACB}=\widehat{CBM}$ (so le trong) (3)
Tương tự MC // AB $(4)$
Từ $(2)$ và $(4)$ theo tính chất cặp đoạn chắn ta có $AC=MB. (5)$
Từ $(1),(3)$ và $(5)$ ta có $\Delta AHC = \Delta MHB$
Do đó $\widehat{MHB}=\widehat{AHC}=\widehat{AHB}=90^o$
Vậy $\widehat{MHB}+\widehat{AHB}=180^o$
Do đó $A,H,M$ thẳng hàng.