K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
BC
1
9 tháng 11 2021
a: Xét (O) có
ΔABC nội tiếp đường tròn
AB là đường kính
Do đó: ΔABC vuông tại C
H
30 tháng 1 2022
\(\left(\dfrac{1}{a^2+a}-\dfrac{1}{a+1}\right):\dfrac{1-a}{a^2+2a+1}=\left(\dfrac{1}{a\left(a+1\right)}-\dfrac{1}{a+1}\right);\dfrac{1-a}{\left(a+1\right)^2}=\left(\dfrac{1}{a\left(a+1\right)}-\dfrac{a}{a\left(a+1\right)}\right):\dfrac{1-a}{\left(a+1\right)^2}=\left(\dfrac{1-a}{a\left(a+1\right)}\right).\dfrac{\left(a+1\right)^2}{1-a}=\dfrac{a+1}{a}\)
27 tháng 9 2021
1b) \(C=\sqrt{81a}-\sqrt{144a}+\sqrt{36a}\left(a\ge0\right)=8\sqrt{a}-12\sqrt{a}+6\sqrt{a}=2\sqrt{a}\)
Bài 2:
a),b) \(P=\left(\dfrac{1}{1-\sqrt{a}}-\dfrac{1}{1+\sqrt{a}}\right)\left(\dfrac{1}{\sqrt{a}}+1\right)\left(đk:x>0,x\ne1\right)\)
\(=\dfrac{1+\sqrt{a}-1+\sqrt{a}}{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}\right)}.\dfrac{\sqrt{a}+1}{\sqrt{a}}=\dfrac{2\sqrt{a}}{1-\sqrt{a}}.\dfrac{1}{\sqrt{a}}=\dfrac{2}{1-\sqrt{a}}\)
c) \(P=\dfrac{2}{1-\sqrt{a}}=\dfrac{2}{1-\sqrt{4}}=\dfrac{2}{1-2}=-2\)
d) \(P=\dfrac{2}{1-\sqrt{a}}=9\)
\(\Rightarrow-9\sqrt{a}+9=2\Rightarrow\sqrt{a}=\dfrac{7}{9}\Rightarrow a=\dfrac{49}{81}\left(tm\right)\)
N
1
24 tháng 6
Câu 6: Để hàm số y=(1-m)x+3 nghịch biến trên R thì 1-m<0
=>m>1
=>Chọn B
Câu 7: D
Câu 10: (D)//(D')
=>\(\left\{{}\begin{matrix}3m+1=2\left(m+1\right)\\-2\ne-2\left(loại\right)\end{matrix}\right.\Leftrightarrow m\in\varnothing\)
=>Chọn D
Câu 11: \(x^2+2x+2=\left(x+1\right)^2+1>=1>0\forall x\)
=>\(\sqrt{x^2+2x+2}\) luôn xác định với mọi số thực x
=>Chọn A
Câu 12: Để hai đường thẳng y=x+3m+2 và y=3x+2m+3 cắt nhau tại một điểm trên trục tung thì \(\left\{{}\begin{matrix}1\ne3\left(đúng\right)\\3m+2=2m+3\end{matrix}\right.\)
=>3m+2=2m+3
=>m=1
=>Chọn C
DT
1
26 tháng 7 2023
1:
a: =12/10-7/10=5/10=1/2
b: \(=\dfrac{4}{13}-\dfrac{4}{13}+\dfrac{-5}{11}-\dfrac{6}{11}=-\dfrac{11}{11}=-1\)
2:
a: x+2/7=-11/7
=>x=-11/7-2/7=-13/7
b: (x+3)/4=-7/2
=>x+3=-14
=>x=-17
3 tháng 10 2021
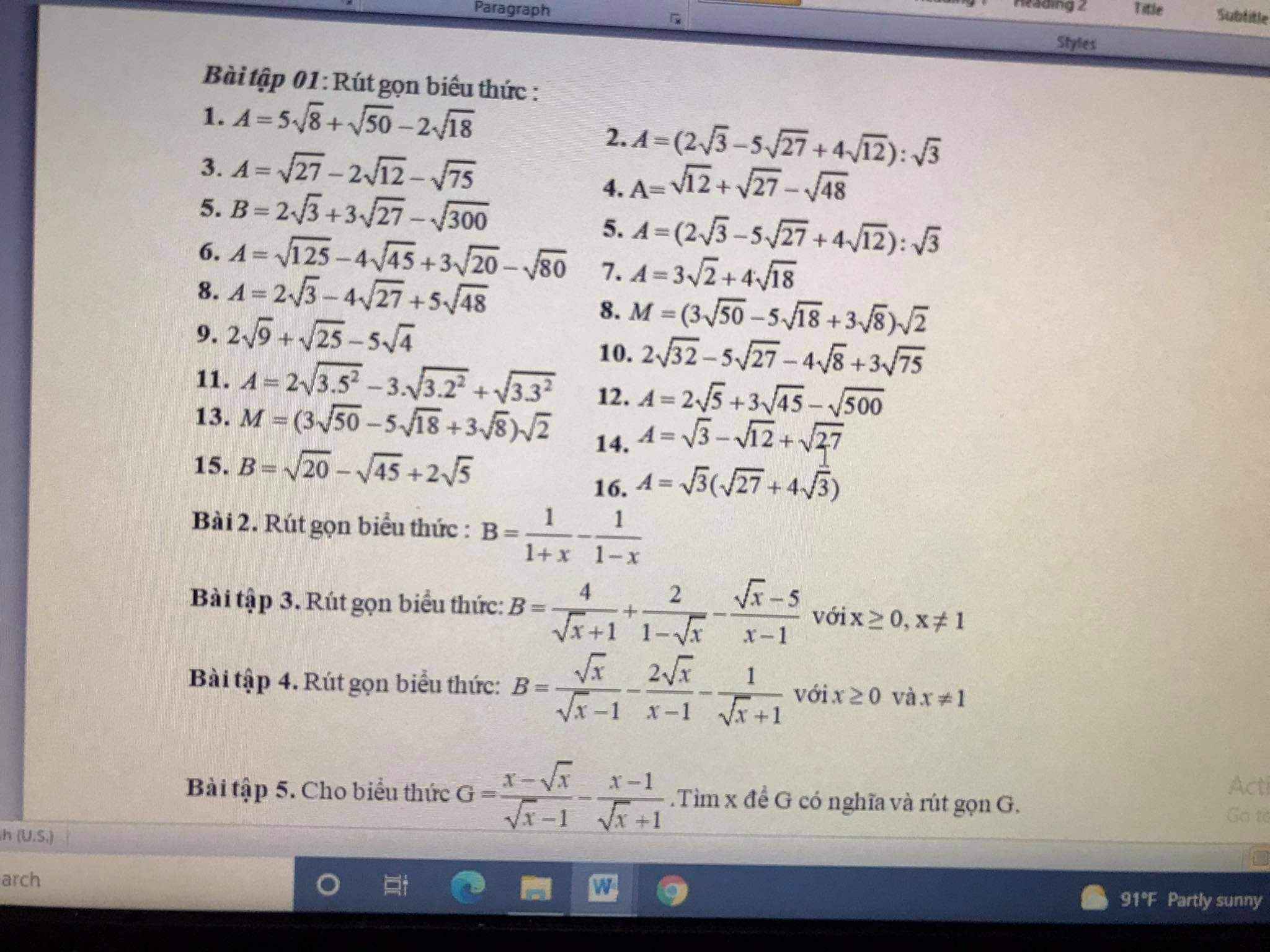
Bài 5:
ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne1\end{matrix}\right.\)
Ta có: \(G=\dfrac{x-\sqrt{x}}{\sqrt{x}-1}-\dfrac{x-1}{\sqrt{x}+1}\)
\(=\sqrt{x}-\sqrt{x}+1\)
=1
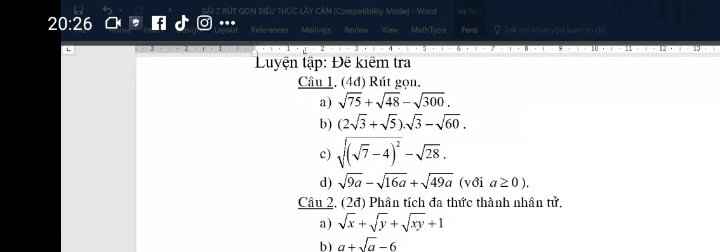
Câu 1:
b: Ta có: \(\left(2\sqrt{3}+\sqrt{5}\right)\cdot\sqrt{3}-\sqrt{60}\)
\(=6+\sqrt{15}-2\sqrt{15}\)
\(=6-\sqrt{15}\)
c: Ta có: \(\sqrt{\left(\sqrt{7}-4\right)^2}-\sqrt{28}\)
\(=4-\sqrt{7}-2\sqrt{7}\)
\(=4-2\sqrt{7}\)