Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Giúp mình giải bài 3 theo cách của lớp 5 với ạ. Cảm ơn mọi người nhiều.
\(\dfrac{S_{AOD}}{S_{DOC}}=\dfrac{10}{20}=\dfrac{1}{2}\)
=>\(AO=\dfrac{1}{2}CO\)
Vì ABCD là hình thang có hai đáy là AB và CD
và AC cắt BD tại O
nên \(S_{AOD}=S_{BOC}\)
=>\(S_{BOC}=10\left(cm^2\right)\)
\(AO=\dfrac{1}{2}OC\)
=>\(S_{AOB}=\dfrac{1}{2}\cdot S_{BOC}=5\left(cm^2\right)\)
\(S_{ABCD}=S_{ABO}+S_{BOC}+S_{DOC}+S_{AOD}\)
\(=5+10+20+10=45\left(cm^2\right)\)
\(\dfrac{13}{2}\) : 4\(\dfrac{2}{3}\): 2
= \(\dfrac{13}{2}\): \(\dfrac{14}{3}\):2
= \(\dfrac{13}{2}\) \(\times\) \(\dfrac{3}{14}\):2
= \(\dfrac{39}{28}\) : 2
= \(\dfrac{39}{28}\) \(\times\) \(\dfrac{1}{2}\)
= \(\dfrac{39}{56}\)
Mình tính từng cái ra nha, từng cái sẽ ra được kết quả của phép tính:
\(1-\dfrac{1}{5}-\dfrac{1}{6}\)
\(=\left(1-\dfrac{1}{5}\right)-\dfrac{1}{6}\)
\(=\left(\dfrac{5}{5}-\dfrac{1}{5}\right)-\dfrac{1}{6}\)
\(=\dfrac{4}{5}-\dfrac{1}{6}\)
\(=\dfrac{24}{30}-\dfrac{5}{30}\)
\(=\dfrac{19}{30}\)
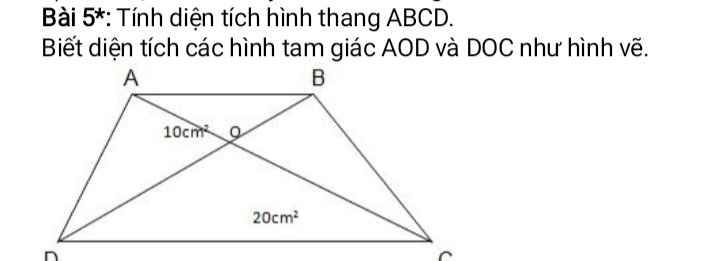
Bài 3:
Nếu đáy lớn được tăng thêm 5 cm thì diện tích sẽ tăng một phần bằng 5 x chiều cao : 2
Vậy chiều cao của hình thang là:
$20\times 2:5=2$ (m)
Diện tích hình thang ban đầu là:
$50\times 2:2=50$ (m2)