
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ủa làm xong bấm nhầm nút.
Không gian mẫu: \(12^3\)
Chọn 2 lần quay từ 3 lần quay: \(C_3^2\)
Có 6 số lẻ và 6 số chẵn nên số cách thỏa mãn là: \(C_3^2.6^2.6\)

a: Gọi (d1): ax+by+c=0 là phương trình đường thẳng cần tìm
(d1) vuông góc (d)
=>(d1): 10x+4y+c=0
Thay x=2 và y=3 vào (d1), ta được:
c+20+12=0
=>c=-32
=>10x+4y-32=0
c: (d): x=1-2t và y=3+4t
=>VTCP là (-2;4)=(-1;2)
=>(d1) có VTPT (-1;2)
mà (d1) đi qua M(2;-3)
nên (d1): -1(x-2)+2(y+3)=0
=>-x+2+2y+6=0
=>-x+2y+8=0
b: (d1) vuông góc (d)
=>(d1): y=0x+b
Thay x=-1 và y=2 vào (d1), ta được:
0*(-1)+b=2
=>b=2
=>(d1): y=2

\(\dfrac{sin^3x+cos^3x}{sinx+cosx}=\dfrac{\left(sinx+cosx\right)\left(sin^2x+cos^2x-sinx.cosx\right)}{sinx+cosx}\)
\(=sin^2x+cos^2x-sinx.cosx=1-sinx.cosx\)

a: (3+x^2)^5
SHTQ là: \(C^k_5\cdot\left(x^2\right)^{5-k}\cdot3^k=C^k_5\cdot x^{10-2k}\cdot3^k\)
SỐ hạng chứa x^4 tương ứng với 10-2k=4
=>k=3
=>Số hạng đó là 270x^4
b: \(\Leftrightarrow\dfrac{\left(n+1\right)!}{\left(n+1-1\right)!\cdot1!}+3\cdot\dfrac{\left(n+2\right)!}{\left(n+2-2\right)!\cdot2!}=\dfrac{\left(n+1\right)!}{\left(n+1-3\right)!\cdot3!}\)
=>\(\left(n+1\right)+3\cdot\dfrac{\left(n+1\right)\left(n+2\right)}{2}=\dfrac{\left(n+1\right)\cdot n\cdot\left(n-1\right)}{6}\)
=>6n+6+9(n^2+3n+2)=n^3-n
=>n^3-n=6n+6+9n^2+27n+18=9n^2+33n+24
=>n^3-9n^2-34n-24=0
=>n=12
(x^2+3)^12
SHTQ là \(C^k_{12}\cdot\left(x^2\right)^{12-k}\cdot3^k=C^k_{12}\cdot3^k\cdot x^{24-2k}\)
Số hạng chứa x^6 tương ứng với 24-2k=6
=>2k=18
=>k=9
=>Hệ số là 4330260

b: \(sin^2b+cos^2b=1\)
=>\(sin^2b=1-\dfrac{1}{5}=\dfrac{4}{5}\)
=>\(sinb=\dfrac{2}{\sqrt{5}}\) hoặc \(sinb=-\dfrac{2}{\sqrt{5}}\)
TH1: \(sinb=\dfrac{2}{\sqrt{5}}\)
\(tanb=\dfrac{2}{\sqrt{5}}:\dfrac{1}{\sqrt{5}}=2\)
cot b=1/tanb=1/2
TH2: \(sinb=-\dfrac{2}{\sqrt{5}}\)
\(tanb=\dfrac{-2}{\sqrt{5}}:\dfrac{1}{\sqrt{5}}=-2\)
cot b=1/tan b=-1/2
c: \(1+cot^2y=\dfrac{1}{sin^2y}\)
=>\(\dfrac{1}{sin^2y}=1+2=3\)
=>\(sin^2y=\dfrac{1}{3}\)
=>\(siny=\dfrac{1}{\sqrt{3}}\) hoặc \(siny=-\dfrac{1}{\sqrt{3}}\)
TH1: \(siny=\dfrac{1}{\sqrt{3}}\)
\(coty=\dfrac{cosy}{siny}\)
=>\(cosy=\dfrac{1}{\sqrt{3}}\cdot\left(-\sqrt{2}\right)=\dfrac{-\sqrt{2}}{\sqrt{3}}\)
\(tany=\dfrac{1}{coty}=\dfrac{-1}{\sqrt{2}}\)
TH2: \(siny=-\dfrac{1}{\sqrt{3}}\)
\(cosy=coty\cdot siny=\left(-\sqrt{2}\right)\cdot\dfrac{-1}{\sqrt{3}}=\dfrac{\sqrt{2}}{\sqrt{3}}=\dfrac{\sqrt{6}}{3}\)
$tany=\frac{1}{coty}=\frac{-1}{\sqrt{2}}$


a: Tọa độ điểm G là:
\(\left\{{}\begin{matrix}x_G=\dfrac{1-4+0}{3}=-1\\y_G=\dfrac{3-1-2}{3}=0\end{matrix}\right.\)
\(\overrightarrow{AB}=\left(-5;-4\right)\)
\(\overrightarrow{AC}=\left(-1;-5\right)\)
Vì \(\overrightarrow{AB}< >\overrightarrow{AC}\) nên ba điểm A,B,C không thẳng hàng
hay ΔABC nhọn


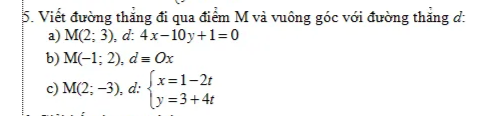


 giúp mình câu b) c) với ạ
giúp mình câu b) c) với ạ

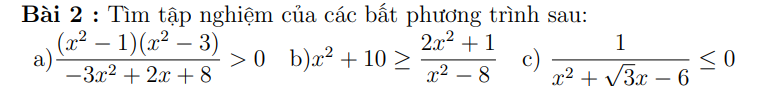
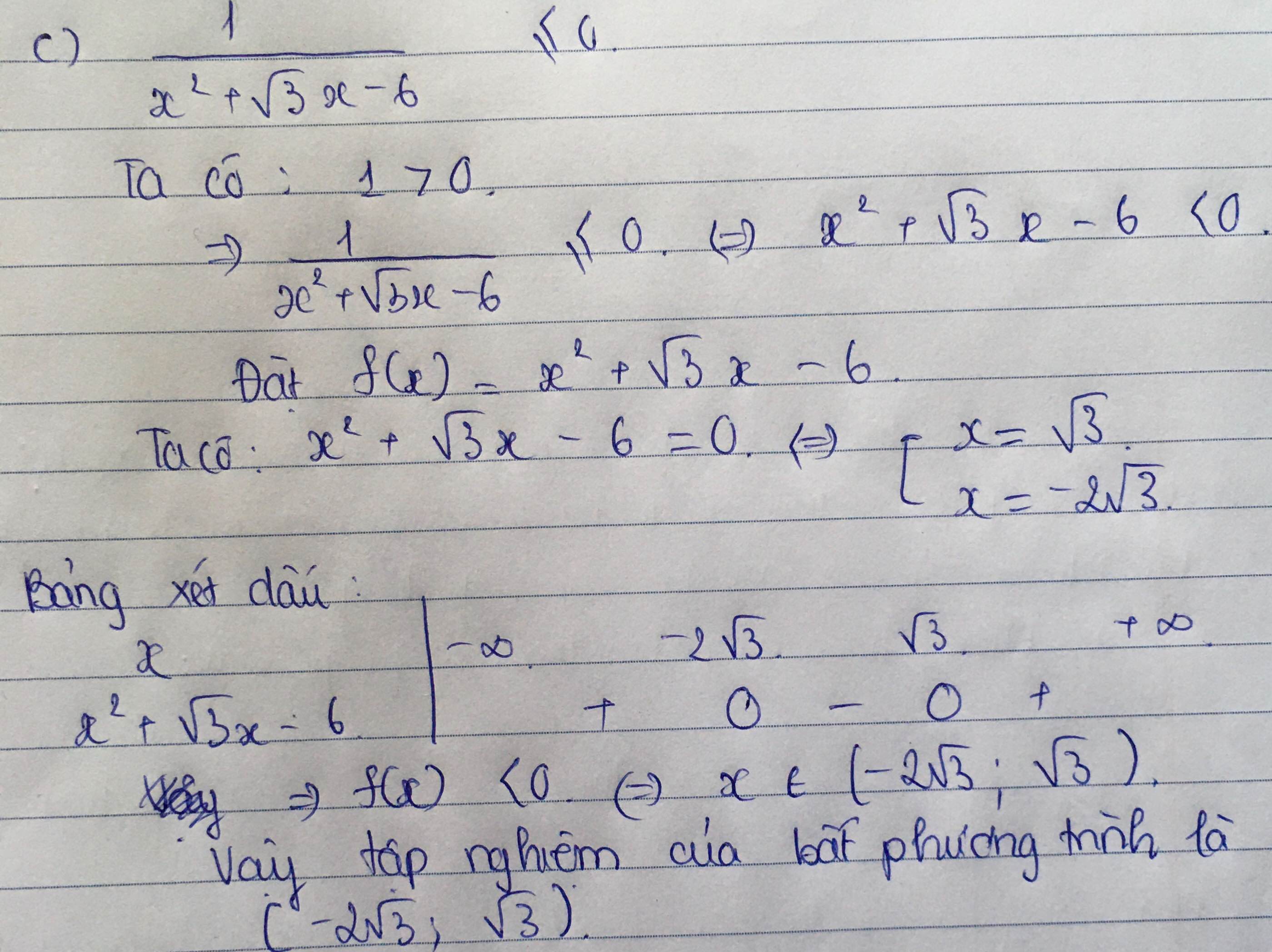
\(\overrightarrow{AB}+\overrightarrow{AC}\) vuông góc \(\overrightarrow{AB}+\overrightarrow{CA}\)
\(\Rightarrow\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\left(\overrightarrow{AB}+\overrightarrow{CA}\right)=0\)
\(\Leftrightarrow\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\left(\overrightarrow{AB}-\overrightarrow{AC}\right)=0\)
\(\Leftrightarrow\overrightarrow{AB}^2-\overrightarrow{AC}^2=0\)
\(\Leftrightarrow AB^2-AC^2=0\)
\(\Leftrightarrow AB=AC\)
Hay tam giác ABC cân tại A
Cách 2: gọi M là trung điểm BC \(\Rightarrow\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AM}\)
Lại có \(\overrightarrow{AB}+\overrightarrow{CA}=\overrightarrow{CB}\)
\(\Rightarrow2\overrightarrow{AM}\perp\overrightarrow{CB}\Rightarrow AM\perp BC\)
\(\Rightarrow\) AM là đường cao đồng thời là trung tuyến
\(\Rightarrow\Delta ABC\) cân tại A