K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
8 tháng 10 2023
46:
(SAB) và (SAD) cùng vuông góc (ABCD)
=>SA vuông góc (ABCD)
=>SA vuông góc AC
ΔSAC vuông tại A
=>\(SC=\sqrt{AS^2+AC^2}=a\sqrt{2}\)
\(V=\dfrac{1}{3}\cdot SA\cdot S_{ABCD}=\dfrac{1}{3}\cdot a\sqrt{2}\cdot a^2=\dfrac{a^3\sqrt{2}}{3}\)
=>Chọn C
47:
\(\dfrac{V_{BC.A'B'C'}}{V_{ABC.A'B'C'}}=\dfrac{2}{3}\)
=>V1=2/3*V
=>Chọn A
48:
AB vuông góc AC
AB vuông góc AD
Do đó: AB vuông góc (ACD)
\(V_{ABCD}=\dfrac{1}{3}\cdot AB\cdot S_{ACD}=\dfrac{1}{3}\cdot5\cdot\dfrac{1}{2}\cdot12\cdot10=100\)
=>Chọn A
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 12 2022
42.
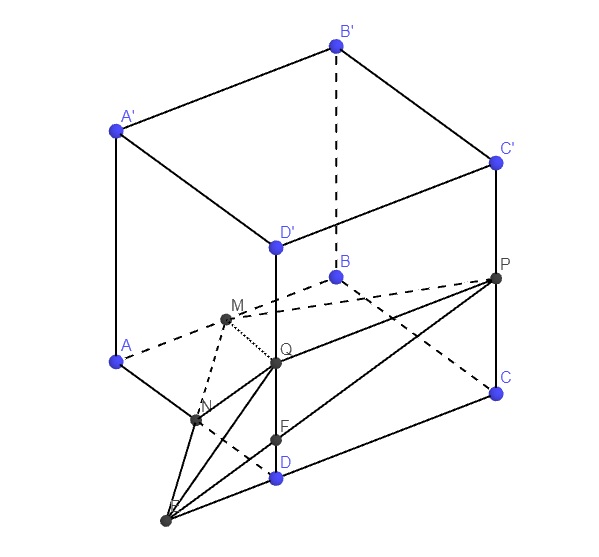
Do mọi hình hộp đều cho kết quả như nhau nên để đơn giản, chúng ta sẽ sử dụng hình hộp chữ nhật để tính toán (với 1 dạng hộp bất kì thì cần kẻ đường cao để tính tỉ lệ, như vậy rất mất thời gian, trong khi sử dụng hộp chữ nhật thì có thể sử dụng trực tiếp cạnh để tính, gọn hơn nhiều):
Nối MN kéo dài cắt CD tại E \(\Rightarrow AM=DE=\dfrac{1}{2}CD\)
Nối PE cắt D'D tại F \(\Rightarrow\dfrac{DF}{CP}=\dfrac{DE}{CE}=\dfrac{1}{3}\Rightarrow DF=\dfrac{1}{3}CP=\dfrac{1}{6}CC'\)
\(\Rightarrow QF=\dfrac{1}{2}CC'-\dfrac{1}{6}CC'=\dfrac{1}{3}CC'\)
\(V_{MNPQ}=V_{M.PQE}-\left(V_{E.NQF}+V_{P.NQF}\right)\)
Có:
\(V_{M.PQE}=\dfrac{1}{3}AD.\dfrac{1}{2}DQ.PQ=\dfrac{1}{12}AD.D'D.CD=\dfrac{1}{12}V\)
\(V_{E.NQF}=\dfrac{1}{3}.ED.\dfrac{1}{2}ND.QF=\dfrac{1}{3}.\dfrac{1}{2}CD.\dfrac{1}{2}.\dfrac{1}{2}AD.\dfrac{1}{3}D'D=\dfrac{1}{72}V\)
\(V_{P.NQF}=\dfrac{1}{3}.PQ.\dfrac{1}{2}ND.QF=\dfrac{1}{3}CD.\dfrac{1}{2}.\dfrac{1}{2}AD.\dfrac{1}{3}D'D=\dfrac{1}{36}V\)
\(\Rightarrow V_{MNPQ}=\dfrac{1}{12}V-\left(\dfrac{1}{72}V+\dfrac{1}{36}V\right)=\dfrac{V}{24}\)
Bài này áp hệ trục tọa độ giải có lẽ sẽ ngắn hơn
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 12 2022
43.
\(y'=2f'\left(2x+m\right)\) có cùng tính đơn điệu với hàm \(f\left(x\right)\)
Mà \(f\left(x\right)\) đồng biến trên \(\left(-1;1\right)\) và \(\left(4;+\infty\right)\)
\(\Rightarrow y=f\left(2x+m\right)\) đồng biến trên các khoảng thỏa mãn:
\(\left[{}\begin{matrix}-1\le2x+m\le1\\2x+m\ge4\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\dfrac{-1-m}{2}\le x\le\dfrac{1-m}{2}\\x\ge\dfrac{4-m}{2}\end{matrix}\right.\)
Hàm đồng biến trên \(\left(1;2\right)\) khi và chỉ khi:
\(\left[{}\begin{matrix}\dfrac{-1-m}{2}\le1< 2\le\dfrac{1-m}{2}\\1\ge\dfrac{4-m}{2}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m=-3\\m\ge2\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 6 2021
84.
Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\BC\perp AB\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp SB\) đồng thời SB là hình chiếu vuông góc của SC lên (SAB)
\(\Rightarrow\widehat{BSC}\) là góc giữa SC và (SAB)
\(\Rightarrow\widehat{BSC}=30^0\)
\(\Rightarrow SB=\dfrac{BC}{tan30^0}=a\sqrt{3}\)
\(\Rightarrow SA=\sqrt{SB^2-AB^2}=a\sqrt{2}\)
\(V=\dfrac{1}{3}SA.BC^2=\dfrac{a^3\sqrt{2}}{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 6 2021
87.
Gọi M là trung điểm BC \(\Rightarrow AM\perp BC\) (trung tuyến đồng thời là đường cao trong tam giác cân)
Mà \(SA\perp\left(ABC\right)\Rightarrow SA\perp BC\)
\(\Rightarrow BC\perp\left(SAM\right)\)
Lại có BC là giao tuyến (SBC) và (ABC)
\(\Rightarrow\widehat{SMA}\) là góc giữa (SBC) và (ABC)
\(\Rightarrow\widehat{SMA}=60^0\)
\(AM=\sqrt{AB^2-BM^2}=\sqrt{4a^2-\left(\dfrac{3a}{2}\right)^2}=\dfrac{a\sqrt{7}}{2}\)
\(SA=AM.tan60^0=\dfrac{a\sqrt{21}}{2}\)
\(V=\dfrac{1}{3}SA.\dfrac{1}{2}.AM.BC=\dfrac{7a^3\sqrt{3}}{8}\)
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 4 2021
Xét \(I_1=2\int\limits^{\dfrac{\pi}{2}}_0f\left(sinx\right)cosxdx=2\int\limits^{\dfrac{\pi}{2}}_0f\left(sinx\right)d\left(sinx\right)\)
Đặt \(sinx=t\Rightarrow t\in\left[0;1\right]\Rightarrow f\left(t\right)=5-t\)
\(I_1=2\int\limits^1_0\left(5-t\right)dt=9\)
Xết \(I_2=3\int\limits^1_0f\left(3-2x\right)dx=-\dfrac{3}{2}\int\limits^1_0f\left(3-2x\right)d\left(3-2x\right)\)
Đặt \(3-2x=t\Rightarrow t\in\left[1;3\right]\Rightarrow f\left(t\right)=t^2+3\)
\(I_2=-\dfrac{3}{2}\int\limits^1_3\left(t^2+3\right)dt=\dfrac{3}{2}\int\limits^3_1\left(t^2+3\right)dt=22\)
\(\Rightarrow I=9+22=31\)
15 tháng 10 2023
\(g'\left(x\right)=\left(-2x\right)'\cdot f'\left(-2x\right)\)
\(=-2\cdot f'\left(-2x\right)\)
\(=-2\left(-2x^2-4x\right)\)
\(=4x^2+8x\)
\(g''\left(x\right)=4\cdot2x+8=8x+8\)
g'(x)=0
=>4x(x+2)=0
=>x=0 hoặc x=-2
Khi x=0 thì \(g''\left(x\right)=8\cdot0+8=8\)>0
=>Khi x=0 thì g(x) đạt giá trị cực đại
Khi x=-2 thì \(g''\left(x\right)=8\cdot\left(-2\right)+8=-8< 0\)
=>Khi x=-2 thì g(x) không đạt giá trị cực đại
Vậy: G(x) đạt giá trị cực đại tại x=0
AH
Akai Haruma
Giáo viên
14 tháng 10 2023
Lời giải:
Bài toán tương đương với:
Tìm $m\in [-10;10]$ để $f(x)=(m+2)x^2-x+3m^2-2m$ với $x\in [0;+\infty)$ có GTLN.
Với $m=-2$ thì $f(x)=-x+16\leq 16$ với mọi $x\geq 0$ nên đạt gtln =16 tại $x=0$
Với $m>-2$ thì $f(x)$ là hàm bậc 2 có hệ số cao nhất dương. Đồng thời $x$ không bị chặn trên nên $f(x)$ không có gtln.
Với $m< -2$ thì $f'(x)=2x(m+2)-1<0$ với mọi $x\geq 0$
$\Rightarrow f(x)$ nghịch biến trên $[0;+\infty)$
$\Rightarrow f(x)\leq f(0)$ tức là hàm số có gtln.
Vậy $m\leq -2$. Tức là $m$ có thể nhận các giá trị $-2, -3, -4, -5, -6, -7, -8, -9,-10$, hay có 9 giá trị $m$ thỏa mãn.
AH
Akai Haruma
Giáo viên
14 tháng 10 2023
Lời giải:
Với hệ số lớn nhất là $1>0$ thì hàm trùng phương chỉ có cực tiểu khi mà:
$y'=4x^3-2(m^2-9)x=0$ có 1 nghiệm duy nhất.
$\Leftrightarrow 2x[2x^2-(m^2-9)]=0$ có nghiệm duy nhất. (*)
Mà pt này đã có sẵn nghiệm $x=0$ nên (*) xảy ra khi mà $2x^2-(m^2-9)=0$ vô nghiệm hoặc có nghiệm $x=0$
$\Leftrightarrow m^2-9=0$ hoặc $m^2-9<0$
$\Leftrightarrow m^2\leq 9$
$\Leftrightarrow -3\leq m\leq 3$
$\Leftrightarrow m\in\left\{-3; -2; -1; 0; 1; 2; 3\right\}$
Tức là có 7 giá trị $m$ nguyên tm.
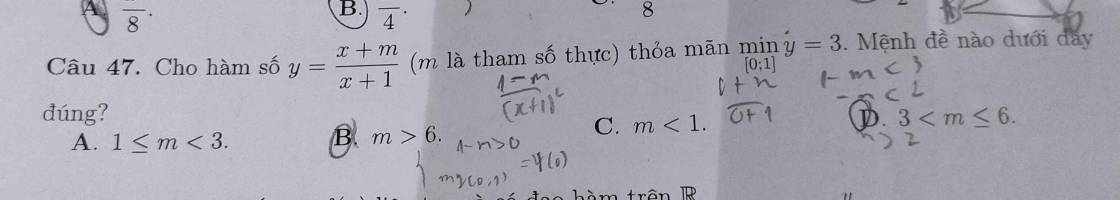
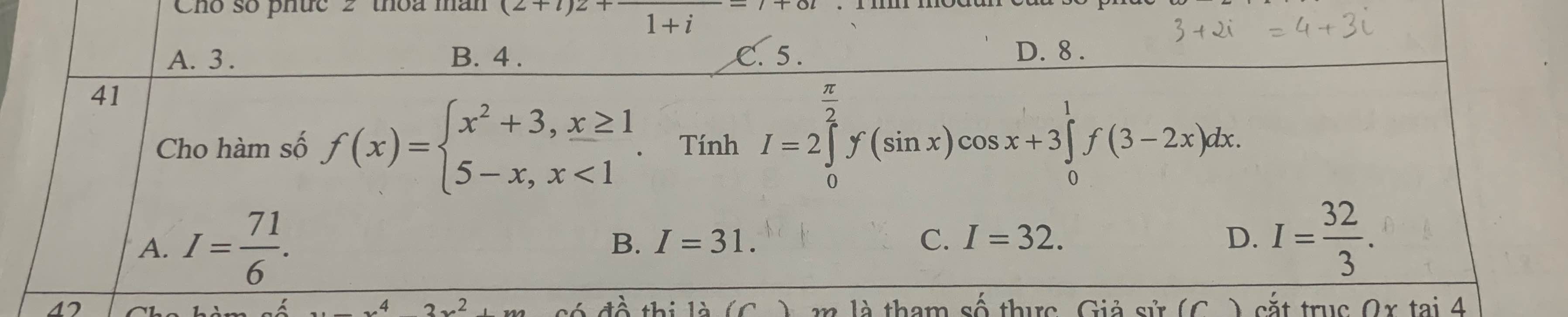
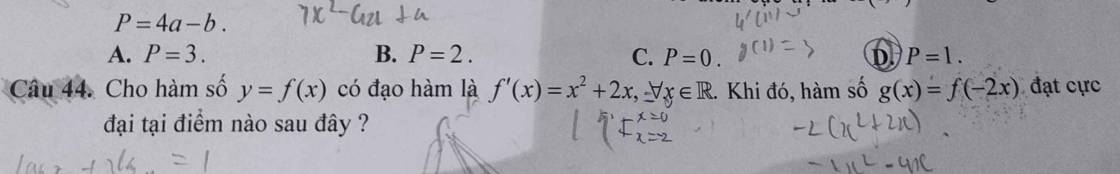
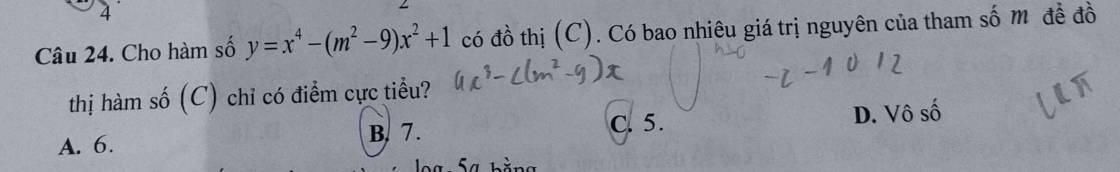
Lời giải:
\(y'=\frac{1-m}{(x+1)^2}\)
Nếu $m=1$ thì $y=1$ với mọi $x\neq -1$ (loại)
Nếu $m> 1$ thì hàm số nghịch biến trên TXĐ
$\Rightarrow$ với $x\in [0;1]$ thì:
$y_{\min}=y(1)=\frac{m+1}{2}=3$
$\Leftrightarrow m=5$
Nếu $m<1$ thì hàm số đồng biến trên TXĐ
$\Rightarrow$ với $x\in [0;1]$ thì:
$y_{\min}=y(0)=\frac{0+m}{0+1}=3\Leftrightarrow m=3$ (vô lý do $m< 1$)
Vậy $m=5$. Nghĩa là đáp án D đúng.