K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
9 tháng 10 2021
\(3,\\ a,ĐK:x\ge-5\\ PT\Leftrightarrow2\sqrt{x+5}-2\sqrt{x+5}+3\sqrt{x+5}=12\\ \Leftrightarrow\sqrt{x+5}=4\Leftrightarrow x+5=16\Leftrightarrow x=11\left(tm\right)\\ b,ĐK:x\in R\\ PT\Leftrightarrow\left|x-5\right|=6\Leftrightarrow\left[{}\begin{matrix}x-5=6\\5-x=6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=11\\x=-1\end{matrix}\right.\)
KT
Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
1
14 tháng 10 2021
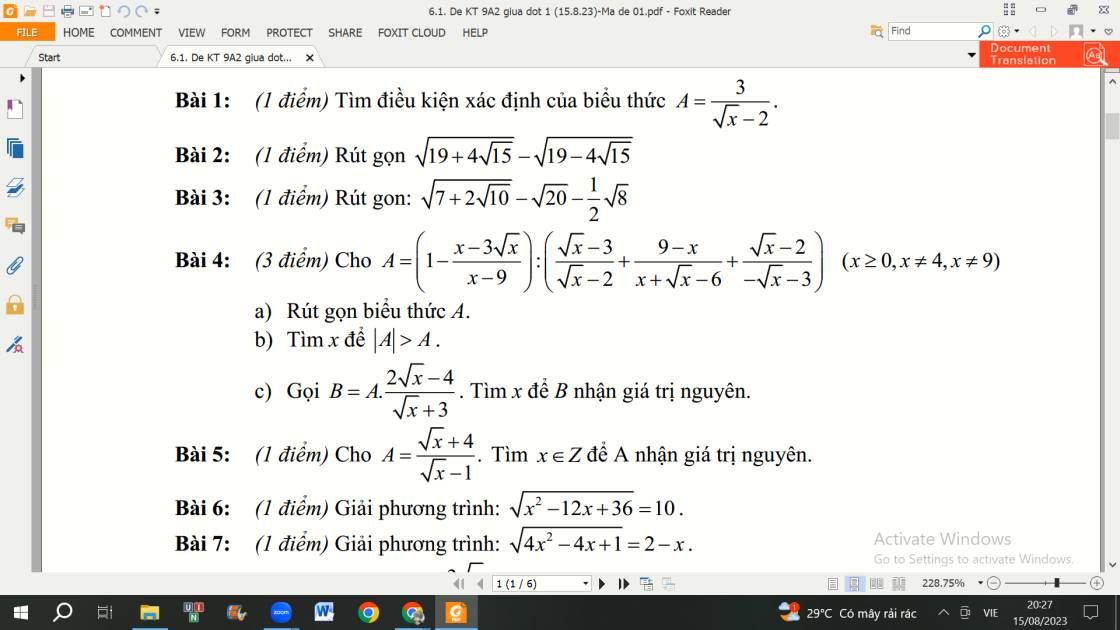
Bài 4:
b: Xét ΔABK vuông tại A có AD là đường cao ứng với cạnh huyền BK
nên \(BD\cdot BK=BA^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(BH\cdot BC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BD\cdot BK=BH\cdot BC\)
11 tháng 11 2023
a: Thay h=65 vào \(d=3,57\sqrt{h}\), ta được:
\(d=3,57\cdot\sqrt{65}\simeq28,78\left(km\right)\)
b: Đặt \(d=30\left(km\right)\)
=>\(3,57\cdot\sqrt{h}=30\)
=>\(\sqrt{h}=\dfrac{30}{3,57}\)
=>\(h\simeq70,62\left(m\right)\)
4 tháng 10 2021
a: \(\sqrt{0.49a^2}=-0.7a\)
b: \(\sqrt{25\left(7-a\right)^2}=5\left(a-7\right)=5a-35\)
c: \(\sqrt{a^4\left(a-2\right)^2}=a^2\left(a-2\right)=a^3-2a^2\)
11 tháng 10 2023
4:
a: \(=3\cdot2\sqrt{3}-4\cdot3\sqrt{3}+5\cdot4\sqrt{3}\)
\(=6\sqrt{3}-12\sqrt{3}+20\sqrt{3}=14\sqrt{3}\)
b: \(=2\sqrt{3}+5\sqrt{3}-3\sqrt{3}=4\sqrt{3}\)
c: \(=2\cdot3\sqrt{2}-7\sqrt{2}+9\sqrt{2}\)
\(=-\sqrt{2}+9\sqrt{2}=8\sqrt{2}\)
d: \(=5\cdot4\sqrt{3}-4\cdot3\sqrt{3}-2\cdot5\sqrt{3}+6\sqrt{3}\)
\(=20\sqrt{3}-12\sqrt{3}-10\sqrt{3}+6\sqrt{3}=4\sqrt{3}\)
21 tháng 7 2021
a, Xét tam giác ABC vuông tại A, đường cao AH
Áp dụng định lí Pytago cho tam giác ABC vuông tại A
\(BC^2=AB^2+AC^2=\dfrac{81}{4}+36=\dfrac{225}{4}\Rightarrow BC=\dfrac{15}{2}\)cm
* Áp dụng hệ thức : \(AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{\dfrac{81}{4}}{\dfrac{15}{2}}=\dfrac{27}{10}\)cm
=> \(CH=BC-BH=\dfrac{15}{2}-\dfrac{27}{10}=\dfrac{24}{5}\)cm
* Áp dụng hệ thức : \(AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}\)
\(=\dfrac{4,5.6}{\dfrac{15}{2}}=\dfrac{18}{5}\)cm
AT
21 tháng 7 2021
tam giác ABC vuông tại A nên áp dụng Py-ta-go
\(\Rightarrow BC^2=AB^2+AC^2=\left(4,5\right)^2+6^2=\dfrac{225}{4}\Rightarrow BC=\dfrac{15}{2}=7,5\left(cm\right)\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{\left(4,5\right)^2}{7,5}=\dfrac{27}{10}=2,7\left(cm\right)\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AC^2=CH.BC\Rightarrow CH=\dfrac{AC^2}{BC}=\dfrac{6^2}{7,5}=\dfrac{24}{5}=4,8\left(cm\right)\)
NL
3