Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a + \(2\sqrt{a-\:1}\)= (a - 1) + \(2\sqrt{a-\:1}\)+ 1 = (\(1\:\:+\sqrt{a-1}\))2
Tương tự cho cái còn lại sẽ ra

a: Kẻ OH vuông góc BC
=>OH là khoảng cách từ O đến BC
ΔOBC cân tại O
mà OH là đường cao
nên H là trung điểm của BC
=>\(HB=HC=\dfrac{BC}{2}=\dfrac{R\sqrt{3}}{2}\)
ΔOHB vuông tại H
=>\(OH^2+HB^2=OB^2\)
=>\(OH^2=OB^2-HB^2=R^2-\left(\dfrac{R\sqrt{3}}{2}\right)^2=\dfrac{R^2}{4}\)
=>OH=R/2
=>d(O;BC)=R/2
b: Xét ΔOBC có \(cosBOC=\dfrac{OB^2+OC^2-BC^2}{2\cdot OB\cdot OC}\)
=>\(cosBOC=\dfrac{R^2+R^2-3R^2}{2\cdot R\cdot R}=\dfrac{-1}{2}\)
=>\(\widehat{BOC}=120^0\)
ΔOBC cân tại O
=>\(\widehat{OBC}=\widehat{OCB}=\dfrac{180^0-120^0}{2}=30^0\)


Câu 4:
D và F cùng nhìn AC dưới 1 góc vuông nên tứ giác ACDF nội tiếp
\(\Rightarrow\widehat{ADF}=\widehat{ACF}\) (cùng chắn AF)
Tương tự, ABDE nội tiếp \(\Rightarrow\widehat{ABE}=\widehat{ADE}\) (cùng chắn AE)
Lại có \(\widehat{ABE}=\widehat{ACF}\) (cùng phụ góc \(\widehat{A}\))
\(\Rightarrow\widehat{ADE}=\widehat{ADF}\) hay AD là phân giác góc \(\widehat{FDE}\)
./
Hoàn toàn tương tự, ta cũng có CF là phân giác \(\widehat{DFE}\Rightarrow\widehat{BFD}=\widehat{AFE}\)
Mà \(\widehat{AFE}=\widehat{BFK}\Rightarrow\widehat{BFK}=\widehat{BFD}\)
\(\Rightarrow\dfrac{BK}{BD}=\dfrac{FK}{FD}\) theo định lý phân giác
Đồng thời \(\dfrac{CK}{CD}=\dfrac{FK}{FD}\) (CF là phân giác ngoài góc \(\widehat{DFK}\))
\(\Rightarrow\dfrac{BK}{BD}=\dfrac{CK}{CD}\Rightarrow\dfrac{BK}{CK}=\dfrac{BD}{CD}\)
Qua B kẻ đường thẳng song song AC cắt AK và AD tại P và Q
Theo Talet: \(\dfrac{BK}{CK}=\dfrac{BP}{AC}\) đồng thời \(\dfrac{BD}{DC}=\dfrac{BQ}{AC}\)
\(\Rightarrow\dfrac{BP}{AC}=\dfrac{BQ}{AC}\Rightarrow BP=BQ\)
Mặt khác BP song song MF (cùng song song AC)
\(\Rightarrow\dfrac{MF}{BP}=\dfrac{AF}{AB}\) ; \(\dfrac{NF}{BQ}=\dfrac{AF}{AB}\) (Talet)
\(\Rightarrow\dfrac{MF}{BP}=\dfrac{NF}{BQ}\Rightarrow MF=NF\)

Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB^2=9\cdot25=225\\AC^2=16\cdot25=400\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=15\left(cm\right)\\AC=20\left(cm\right)\end{matrix}\right.\)
Xét ΔABC vuông tại A có
\(\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{15}{25}=\dfrac{3}{5}\)
\(\Leftrightarrow\widehat{C}\simeq37^0\)
\(\Leftrightarrow\widehat{B}=53^0\)

a: góc AEB=góc AHB=90 độ
=>ABHE nôi tiếp
b: Gọi N là trung điểm của AB
=>AN=HN=EN=BN
MN là đường trung bình của ΔABC
=>MN//AC
HE vuông góc AC
=>HE vuông góc MN
=>MN là trung trực của HE
=>ME=MH

a) \(A=\sqrt{1-x}+\sqrt{1+x}\)
\(\Rightarrow A^2=1-x+1+x+2\sqrt{\left(1-x\right)\left(1+x\right)}=2+2\sqrt{1-x^2}\)
Do \(-x^2\le0\Rightarrow1-x^2\le1\Rightarrow A^2=2+2\sqrt{1-x^2}\le2+2=4\)
\(\Rightarrow A\le2\)
\(maxA=2\Leftrightarrow x=0\)
Áp dụng bất đẳng thức: \(\sqrt{x}+\sqrt{y}\ge\sqrt{x+y}\)(với \(x,y\ge0\))
\(\Leftrightarrow\left(\sqrt{x}+\sqrt{y}\right)^2\ge x+y\)
\(\Leftrightarrow x+y+2\sqrt{xy}\ge x+y\Leftrightarrow2\sqrt{xy}\ge0\left(đúng\right)\)
\(A=\sqrt{1-x}+\sqrt{1+x}\ge\sqrt{1-x+1+x}=\sqrt{2}\)
\(maxA=\sqrt{2}\Leftrightarrow\)\(\left[{}\begin{matrix}1-x=0\\1+x=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)

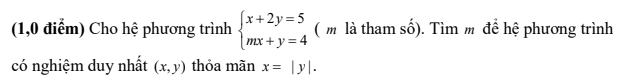 gíup e vs ạ hiu hiu
gíup e vs ạ hiu hiu 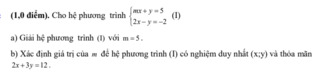






2:
a: Xét tứ giác OAMD có
\(\widehat{OAM}+\widehat{ODM}=90^0+90^0=180^0\)
=>OAMD là tứ giác nội tiếp
b: Xét (O) có
ΔADC nội tiếp
AC là đường kính
Do đó: ΔADC vuông tại D
=>AD\(\perp\)BC tại D
Xét ΔABC vuông tại A có AD là đường cao
nên \(AD^2=DB\cdot DC\)
Xét (O) có
MA,MD là tiếp tuyến
Do đó: MA=MD
=>\(\widehat{MAD}=\widehat{MDA}\)
mà \(\widehat{MAD}+\widehat{MBD}=90^0\)(ΔADB vuông tại D)
và \(\widehat{MDA}+\widehat{MDB}=\widehat{BDA}=90^0\)
nên \(\widehat{MDB}=\widehat{MBD}\)
=>MD=MB
mà MD=MA
nên MB=MA
=>M là trung điểm của AB
Xét ΔABC có
M,O lần lượt là trung điểm của AB,AC
=>MO là đường trung bình
=>MO//BC