Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1:
Xét ΔABC vuông tại A có
\(tanB=\dfrac{AC}{AB}\)
=>\(\dfrac{AC}{6}=\dfrac{4}{3}\)
=>\(AC=\dfrac{4}{3}\cdot6=8\left(cm\right)\)
Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=100\)
=>\(BC=\sqrt{100}=10\left(cm\right)\)
Câu 4:
a: Thay x=2 và y=5 vào y=(2m-1)x+3, ta được:
2(2m-1)+3=5
=>2(2m-1)=2
=>2m-1=1
=>2m=2
=>\(m=\dfrac{2}{2}=1\)
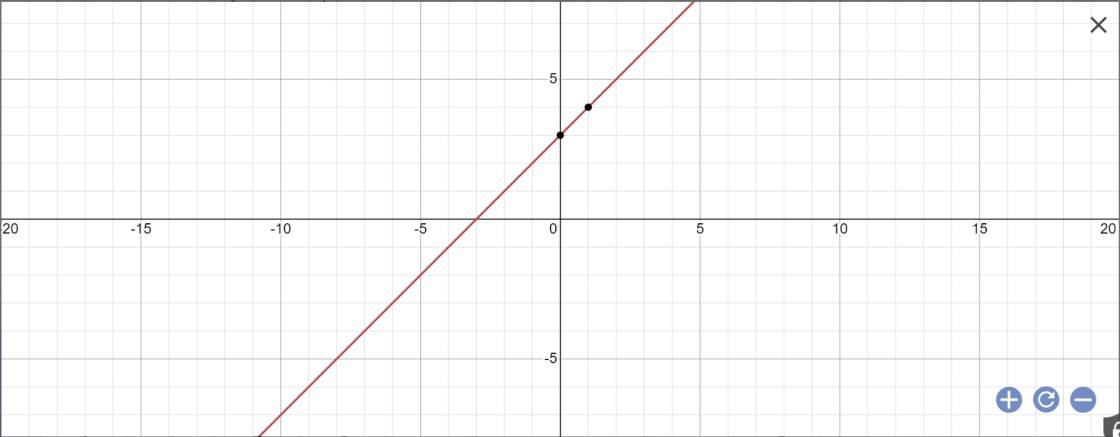
b: Khi m=1 thì \(y=\left(2\cdot1-1\right)x+3=x+3\)

Câu 1:
Gọi giao điểm của OC với AB là H
Vì OC\(\perp\)AB nên OH\(\perp\)AB tại H
=>OH là khoảng cách từ O xuống dây AB
Ta có: ΔOAB cân tại O
mà OH là đường cao
nên H là trung điểm của AB
=>HA=HB=AB/2=8(cm)
ΔOHA vuông tại H
=>\(OH^2+HA^2=OA^2\)
=>\(OH^2=10^2-8^2=36\)
=>\(OH=\sqrt{36}=6\left(cm\right)\)
Câu 2:
a: Xét (O) có
AB là đường kính
BC là dây
Do đó: AB>BC
b: Xét (O) có
ΔCAB nội tiếp
AB là đường kính
Do đó: ΔCAB vuông tại C
c: Xét ΔACB có
O là trung điểm của AB
OM//CB
Do đó: M là trung điểm của AC

a, A n B ⏜ - cung lớn; A m B ⏜ - cung nhỏ
Vì sđ A n B ⏜ + sđ A m B ⏜ = 360 0 ; mà sđ A n B ⏜ = 3sđ A m B ⏜
nên sđ A n B ⏜ = 270 0 và độ dài cung A n B ⏜ là l = 3 πR 2
b, Vì DOAB vuông cân => A O B ^ = 90 0 và O A B ^ = O B A ^ = 45 0
c, Vì AB = R 2 => OH = R 2 2 (OH ⊥ AB; H ∈ AB)
a: Kẻ OH vuông góc BC
=>OH là khoảng cách từ O đến BC
ΔOBC cân tại O
mà OH là đường cao
nên H là trung điểm của BC
=>\(HB=HC=\dfrac{BC}{2}=\dfrac{R\sqrt{3}}{2}\)
ΔOHB vuông tại H
=>\(OH^2+HB^2=OB^2\)
=>\(OH^2=OB^2-HB^2=R^2-\left(\dfrac{R\sqrt{3}}{2}\right)^2=\dfrac{R^2}{4}\)
=>OH=R/2
=>d(O;BC)=R/2
b: Xét ΔOBC có \(cosBOC=\dfrac{OB^2+OC^2-BC^2}{2\cdot OB\cdot OC}\)
=>\(cosBOC=\dfrac{R^2+R^2-3R^2}{2\cdot R\cdot R}=\dfrac{-1}{2}\)
=>\(\widehat{BOC}=120^0\)
ΔOBC cân tại O
=>\(\widehat{OBC}=\widehat{OCB}=\dfrac{180^0-120^0}{2}=30^0\)
cảm ơn nha