
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


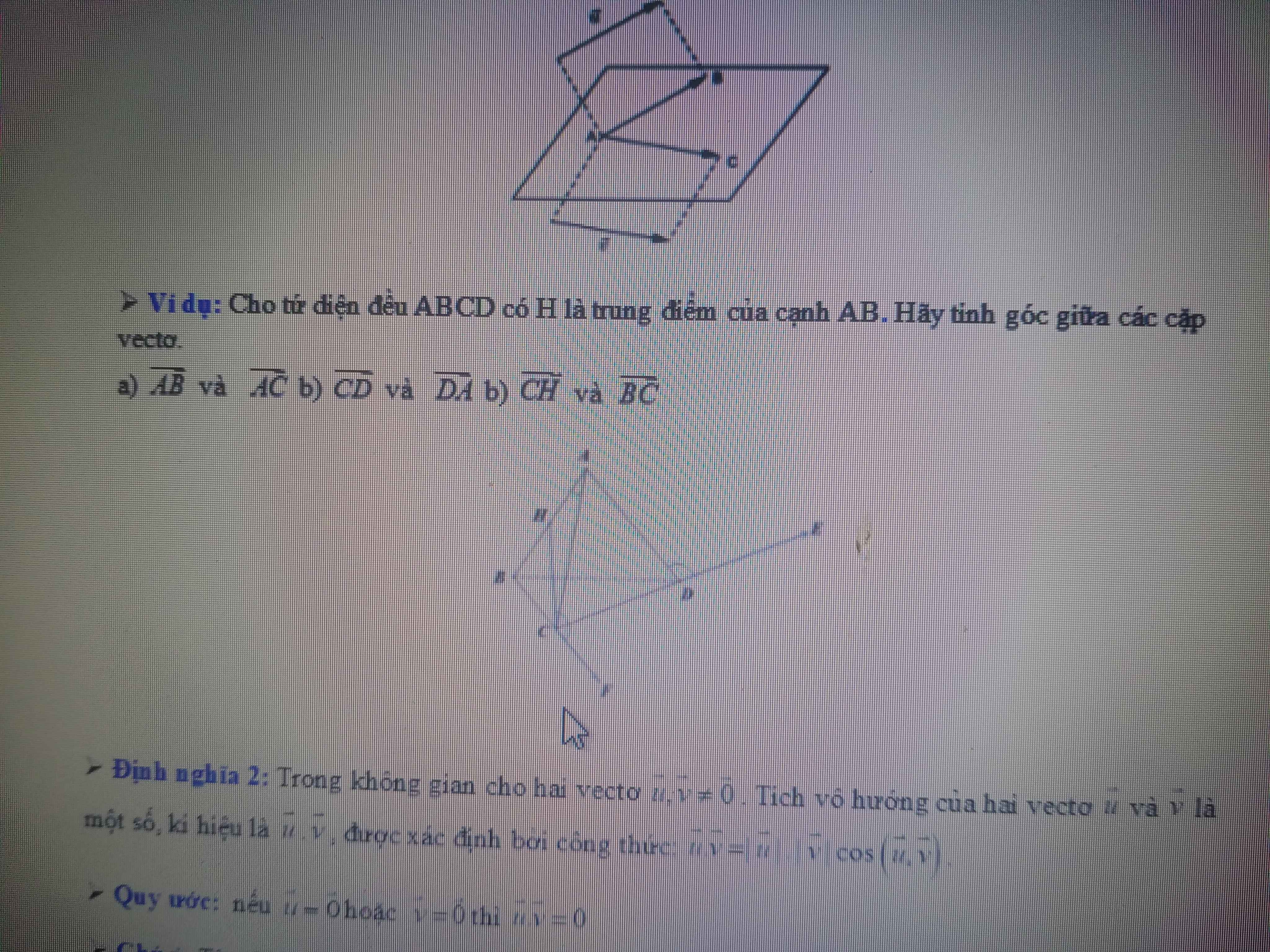
a: \(\left(\overrightarrow{AB};\overrightarrow{AC}\right)=\widehat{BAC}=60^0\)
b: Kẻ vecto DE=vecto CD
=>góc ADE=120 độ
(vecto CD;vecto DA)=(vecto DE;vecto DA)=góc ADE=120 độ
c: góc ACH=góc BCH=60/2=30 độ
Lấy F sao cho vecto BC=vecto CF
=>góc HCF=180-30=150 độ
(vecto CH;vecto BC)=(vecto CH;vecto CF)=150 độ

a: y'=3x^2-3*2x+1=3x^2-6x+1
b: y'=1/3*3x^2+1/x^2+1/2*căn x=x^2+1/x^2+1/2*căn x
c: y'=(x-3)'*(x^2+2)+(x-3)*(x^2+2)'
=x^2+2+2x(x-3)=2x^2-6x+x^2+2=3x^2-6x+2
f: y'=10*(2x-5)^9*(2x-5)'=20(2x-5)^9


Ớ :D? Này hình như là đề thi chọn HSG Quốc gia môn Toán đúng ko nhờ :D? Thằng bạn kêu tui làm thử mà nhìn đề xong tui shock nặng luôn :b Lót dép hóng ai đó làm :3
Ò đúng rồi, đề thi HSG đó, con bạn mình nó kêu đi hỏi hộ nó để nó so keys, cơ mà thôi chắc không cần nữa rồi :v

\(\dfrac{1}{2}sin6x\ne0\)\(\Leftrightarrow sin6x\ne0\) \(\Leftrightarrow6x\ne k\pi\)\(\Leftrightarrow x\ne\dfrac{k\pi}{6}\)
\(\dfrac{1}{2}\ne0\) rồi nên chỉ cần \(sin6x\ne0\)

1.
\(\Leftrightarrow\sqrt{2}sin\left(x-\dfrac{\pi}{4}\right)=0\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{4}\right)=0\)
\(\Leftrightarrow x-\dfrac{\pi}{4}=k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{4}+k\pi\)
2.
\(\Leftrightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=1\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{4}=\dfrac{\pi}{4}+k2\pi\\x+\dfrac{\pi}{4}=\dfrac{3\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)
3.
\(\Leftrightarrow\left(sin^2x+cos^2x\right)^2-2sin^2x.cos^2x=\dfrac{5}{8}\)
\(\Leftrightarrow1-\dfrac{1}{2}sin^22x=\dfrac{5}{8}\)
\(\Leftrightarrow1-\dfrac{1}{2}\left(\dfrac{1}{2}-\dfrac{1}{2}cos4x\right)=\dfrac{5}{8}\)
\(\Leftrightarrow\dfrac{3}{4}+\dfrac{1}{4}cos4x=\dfrac{5}{8}\)
\(\Leftrightarrow cos4x=-\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}4x=\dfrac{2\pi}{3}+k2\pi\\4x=-\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+\dfrac{k\pi}{2}\\x=-\dfrac{\pi}{6}+\dfrac{k\pi}{2}\end{matrix}\right.\)
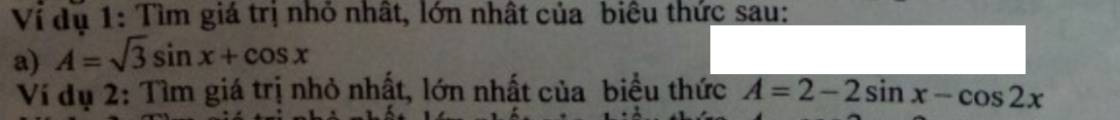


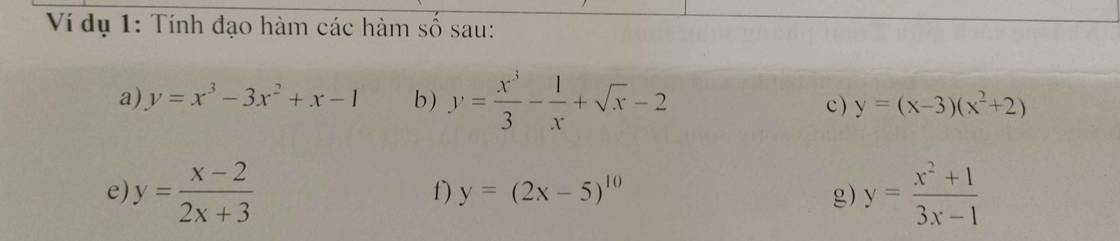



Ví dụ 1:
a)
Đạo hàm của biểu thức A theo x:
`A' = (√3cosx - sinx)`
Giải phương trình A' = 0:
`(√3cosx - sinx) = 0`
`⇒ √3cosx = sinx`
`⇒ 3cos^2x = sin^2x` (bình phương hai vế)
`⇒ 3(1 - sin^2x) = sin^2x` (sử dụng công thức `cos^2x = 1 - sin^2x`)
`⇒ 3 - 3sin^2x = sin^2x`
`⇒ 4sin^2x = 3`
`⇒ sin^2x = 3/4`
`⇒ sinx = ±√(3/4) = ±√3/2`
Với `sinx = √3/2`, ta có `cosx = √(1 - sin^2x) = √(1 - 3/4) = √1/4 = 1/2`
Với `sinx = -√3/2`, ta có `cosx = √(1 - sin^2x) = √(1 - 3/4) = √1/4 = 1/2`
Vậy, giá trị nhỏ nhất của biểu thức A là:
`A(min) = √3sinx + cosx = √3(√3/2) + 1/2 = 3/2 + 1/2 = 2`
Giá trị lớn nhất của biểu thức A cũng là `2`