
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




b: Để phương trình có hai nghiệm cùng dấu thì
\(\left\{{}\begin{matrix}4m^2-4\left(m-2\right)\left(m+1\right)>0\\\dfrac{m+1}{m-2}>0\\\dfrac{-2m}{m-2}>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4m^2-4m^2+4m+8>0\\m>2\\0< m< 2\end{matrix}\right.\Leftrightarrow m>2\)



Câu 2:
\(a,\Leftrightarrow\Delta'=\left(1-m\right)^2-\left(m^2-m\right)>0\\ \Leftrightarrow m^2-2m+1-m^2+m>0\\ \Leftrightarrow1-m>0\Leftrightarrow m< 1\\ b,\text{Áp dụng Viét: }\left\{{}\begin{matrix}x_1+x_2=2\left(1-m\right)\\x_1x_2=m^2-m\end{matrix}\right.\\ \left(2x_1-1\right)\left(2x_2-1\right)-x_1x_2=1\\ \Leftrightarrow2x_1x_2-2\left(x_1+x_2\right)+1-x_1x_2=1\\ \Leftrightarrow x_1x_2-2\left(x_1+x_2\right)=0\\ \Leftrightarrow m^2-m-4\left(1-m\right)=0\\ \Leftrightarrow m^2+3m-4=0\\ \Leftrightarrow\left(m-1\right)\left(m+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}m=1\left(ktm\right)\\m=-4\left(tm\right)\end{matrix}\right.\)
Vậy m=-4
Câu 1:
\(1,\Leftrightarrow2x-2=3\Leftrightarrow x=\dfrac{5}{2}\\ 2,ĐK:x\ne\pm1\\ PT\Leftrightarrow\dfrac{2x^2+2x-1}{x^2-1}=2\\ \Leftrightarrow2x^2+2x-1=2x^2-2\\ \Leftrightarrow2x=-1\Leftrightarrow x=-\dfrac{1}{2}\left(tm\right)\\ 3,\Leftrightarrow\left[{}\begin{matrix}3x-2=2x-1\\3x-2=1-2x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{3}{5}\end{matrix}\right.\)
\(4,\Leftrightarrow\left[{}\begin{matrix}3x-1=2-x\left(x\ge\dfrac{1}{3}\right)\\3x-1=x-2\left(x< \dfrac{1}{3}\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{4}\left(tm\right)\\x=-\dfrac{1}{2}\left(tm\right)\end{matrix}\right.\\ 5,\Leftrightarrow4x^2-2x+10=9x^2-6x+1\left(x\le\dfrac{1}{3}\right)\\ \Leftrightarrow5x^2-4x-9=0\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{9}{5}\left(ktm\right)\\x=-1\left(tm\right)\end{matrix}\right.\)
\(6,\Leftrightarrow3x^2-9x+1=x^2-4x+4\left(x\ge2\right)\\ \Leftrightarrow2x^2-5x-3=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3\left(tm\right)\\x=-\dfrac{1}{2}\left(ktm\right)\end{matrix}\right.\\ 7,\Leftrightarrow2x^2+3x-4=7x+2\left(x\ge-\dfrac{2}{7}\right)\\ \Leftrightarrow x^2-2x-3=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3\left(tm\right)\\x=-1\left(ktm\right)\end{matrix}\right.\)


\(\Leftrightarrow\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}+3\ge\dfrac{2\left(a+b+c\right)}{abc}=2\left(\dfrac{1}{ab}+\dfrac{1}{ac}+\dfrac{1}{bc}\right)\)
Đặt \(\left(\dfrac{1}{a};\dfrac{1}{b};\dfrac{1}{c}\right)=\left(x;y;z\right)\Rightarrow xyz=1\)
BĐT trở thành: \(x^2+y^2+z^2+3\ge2\left(xy+yz+zx\right)\)
Theo nguyên lý Dirichlet, trong 3 số x;y;z luôn có ít nhất 2 số cùng phía so với 1
Không mất tính tổng quát, giả sử đó là x và y \(\Rightarrow\left(x-1\right)\left(y-1\right)\ge0\)
\(\Rightarrow xy+1\ge x+y\Rightarrow xyz+z\ge xz+yz\Rightarrow2xyz+2z\ge2xz+2yz\)
\(\Rightarrow2\ge2xz+2yz-2z\) (do \(xyz=1\))
\(\Rightarrow VP=x^2+y^2+z^2+2+1\ge x^2+y^2+z^2+2xz+2yz-2z+1\)
\(VP\ge2xy+z^2+2xz+2yz-2z+1=2\left(xy+yz+zx\right)+\left(z-1\right)^2\ge2\left(xy+yz+zx\right)\) (đpcm)
Dấu "=" xảy ra khi \(x=y=z=1\) hay \(a=b=c=1\)

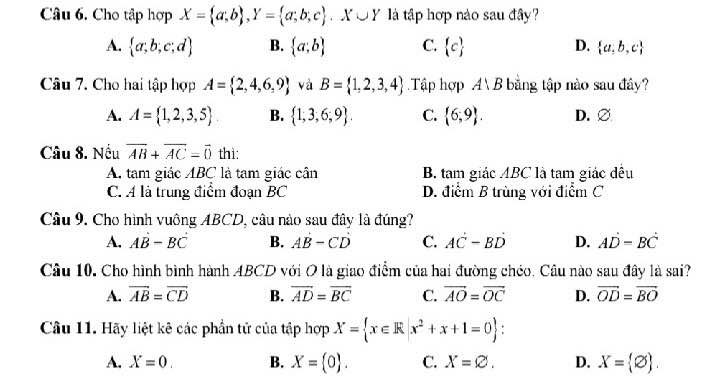






 giúp e với m.n ơiii
giúp e với m.n ơiii
Câu 7: D
Câu 8: A
Câu 9: A