
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: ĐKXĐ: \(x\notin\left\{3;-3;-1\right\}\)
\(A=\dfrac{x\left(x-3\right)-2\left(x+3\right)-x^2+1}{x^2-9}:\dfrac{2x+6-x-5}{x+3}\)
\(=\dfrac{x^2-3x-2x-6-x^2+1}{\left(x-3\right)\left(x+3\right)}\cdot\dfrac{x+3}{x+1}\)
\(=\dfrac{-5\left(x+1\right)}{\left(x-3\right)}\cdot\dfrac{1}{x+1}=-\dfrac{5}{x-3}\)
b: \(x^2-x-2=0\)
=>\(\left(x-2\right)\left(x+1\right)=0\)
=>\(\left[{}\begin{matrix}x=2\left(nhận\right)\\x=-1\left(loại\right)\end{matrix}\right.\)
Khi x=2 thì \(A=\dfrac{-5}{2-3}=\dfrac{-5}{-1}=5\)
c: A=1/2
=>\(-\dfrac{5}{x-3}=\dfrac{1}{2}\)
=>x-3=-10
=>x=-7(nhận)


a: Xét (O) có
CM,CA là các tiếp tuyến
Do đó: CM=CA và OC là phân giác của góc MOA
Xét (O) có
DM,DB là các tiếp tuyến
Do đó: DM=DB và OD là phân giác của góc MOB
Ta có: CD=CM+MD
mà CM=CA và DM=DB
nên CD=CA+DB
Ta có: OC là phân giác của góc MOA
=>\(\widehat{MOA}=2\cdot\widehat{MOC}\)
Ta có: OD là phân giác của góc MOB
=>\(\widehat{MOB}=2\cdot\widehat{MOD}\)
Ta có: \(\widehat{MOA}+\widehat{MOB}=180^0\)(hai góc kề bù)
=>\(2\cdot\left(\widehat{MOC}+\widehat{MOD}\right)=180^0\)
=>\(2\cdot\widehat{COD}=180^0\)
=>\(\widehat{COD}=90^0\)
b: Xét ΔOCD vuông tại O có OM là đường cao
nên \(MC\cdot MD=OM^2\)
mà MC=CA và MD=DB
nên \(CA\cdot DB=OM^2=R^2\)
c: Xét (O) có
\(\widehat{MAB}\) là góc nội tiếp chắn cung MB
=>\(\widehat{MAB}=\dfrac{1}{2}\cdot sđ\stackrel\frown{MB}\)
=>\(\widehat{MOB}=2\cdot\widehat{MAB}=120^0\)
Xét tứ giác OBDM có
\(\widehat{OBD}+\widehat{D}+\widehat{DMO}+\widehat{MOB}=360^0\)
=>\(\widehat{D}+120^0+90^0+90^0=360^0\)
=>\(\widehat{D}=60^0\)
Xét ΔDMB có DM=DB và \(\widehat{D}=60^0\)
nên ΔDMB đều

Sửa đề: \(-3x+\sqrt{25x^2}\)
\(=-3x+\sqrt{\left(5x\right)^2}\)
\(=-3x-5x\left(x< 0\right)\)
=-8x
=>Chọn C

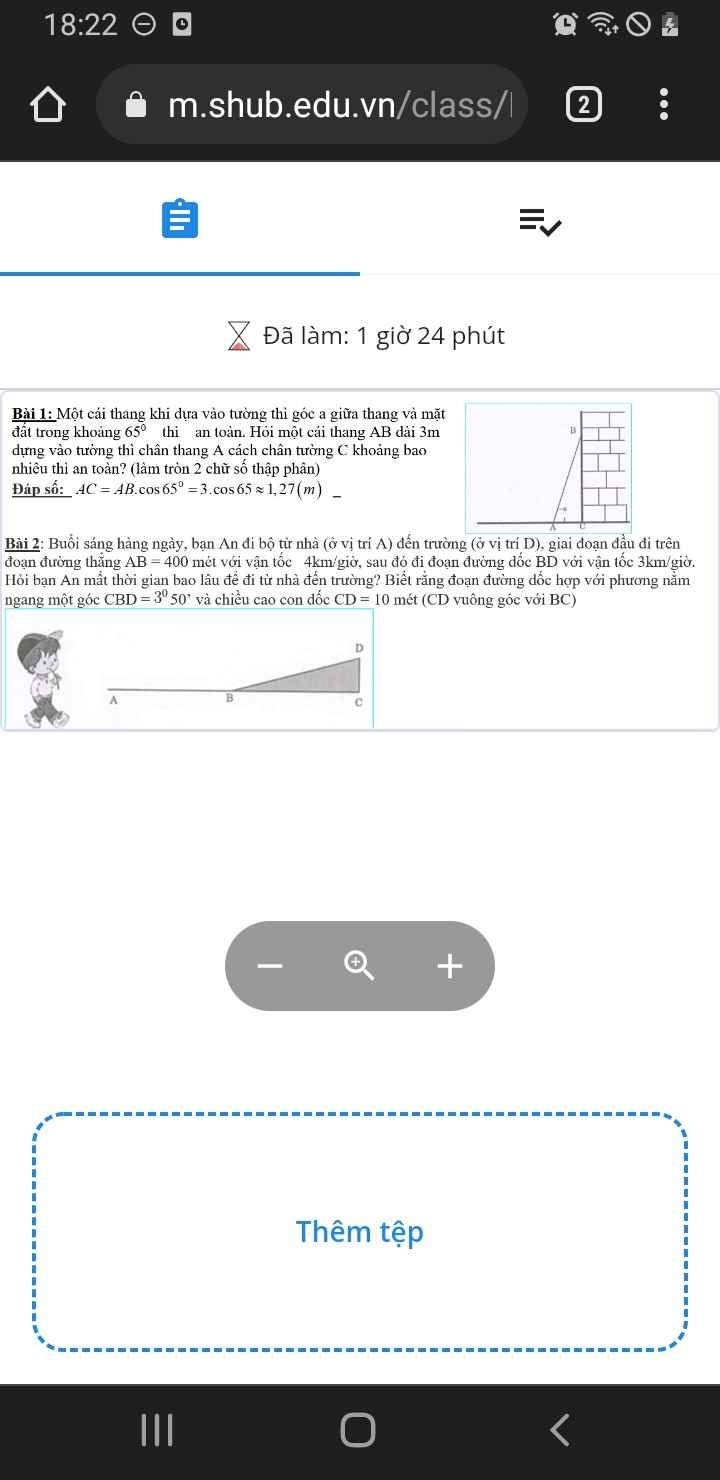
Độ dài quãng đường BD:
\(BD=\dfrac{CD}{sin\widehat{CBD}}=\dfrac{10}{sin3^050'}\approx150\left(m\right)=0,15\left(km\right)\)
Thời gian đi hết đoạn AB:
\(t_1=\dfrac{0,4}{4}=0,1\left(h\right)\)
Thời gian đi hết đoạn BD:
\(t_2=\dfrac{0,15}{3}=0,05\left(h\right)\)
Tổng thời gian:
\(t=t_1+t_2=0,15\left(h\right)=9\left(ph\right)\)

1.2 với \(x\ge0,x\in Z\)
A=\(\dfrac{2\sqrt{x}+7}{\sqrt{x}+2}=2+\dfrac{3}{\sqrt{x}+2}\in Z< =>\sqrt{x}+2\inƯ\left(3\right)=\left(\pm1;\pm3\right)\)
*\(\sqrt{x}+2=1=>\sqrt{x}=-1\)(vô lí)
*\(\sqrt{x}+2=-1=>\sqrt{x}=-3\)(vô lí
*\(\sqrt{x}+2=3=>x=1\)(TM)
*\(\sqrt{x}+2=-3=\sqrt{x}=-5\)(vô lí)
vậy x=1 thì A\(\in Z\)

6:
1: BH=căn 15^2-12^2=9cm
BC=15^2/9=25cm
AC=căn 25^2-15^2=20cm
C ABC=15+20+25=60cm
XétΔHAB vuông tại H có sin BAH=BH/AB=9/15=3/5
nên góc BAH=37 độ
2: ΔABC vuông tại A có AH là đường cao
nên CA^2=CH*CB
ΔCAH vuông tại H có HF là đường cao
nên CF*CA=CA^2=CH*CB
3: Xét tứ giác AFHB có
HF//AB
góc AFH=90 độ
=>AFHB là hình thang vuông
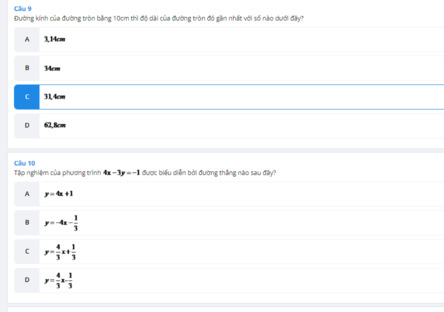
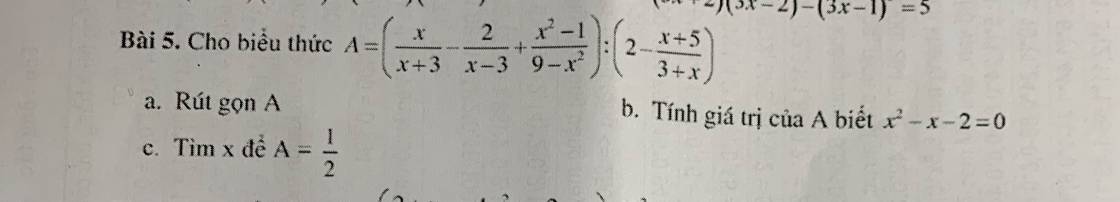



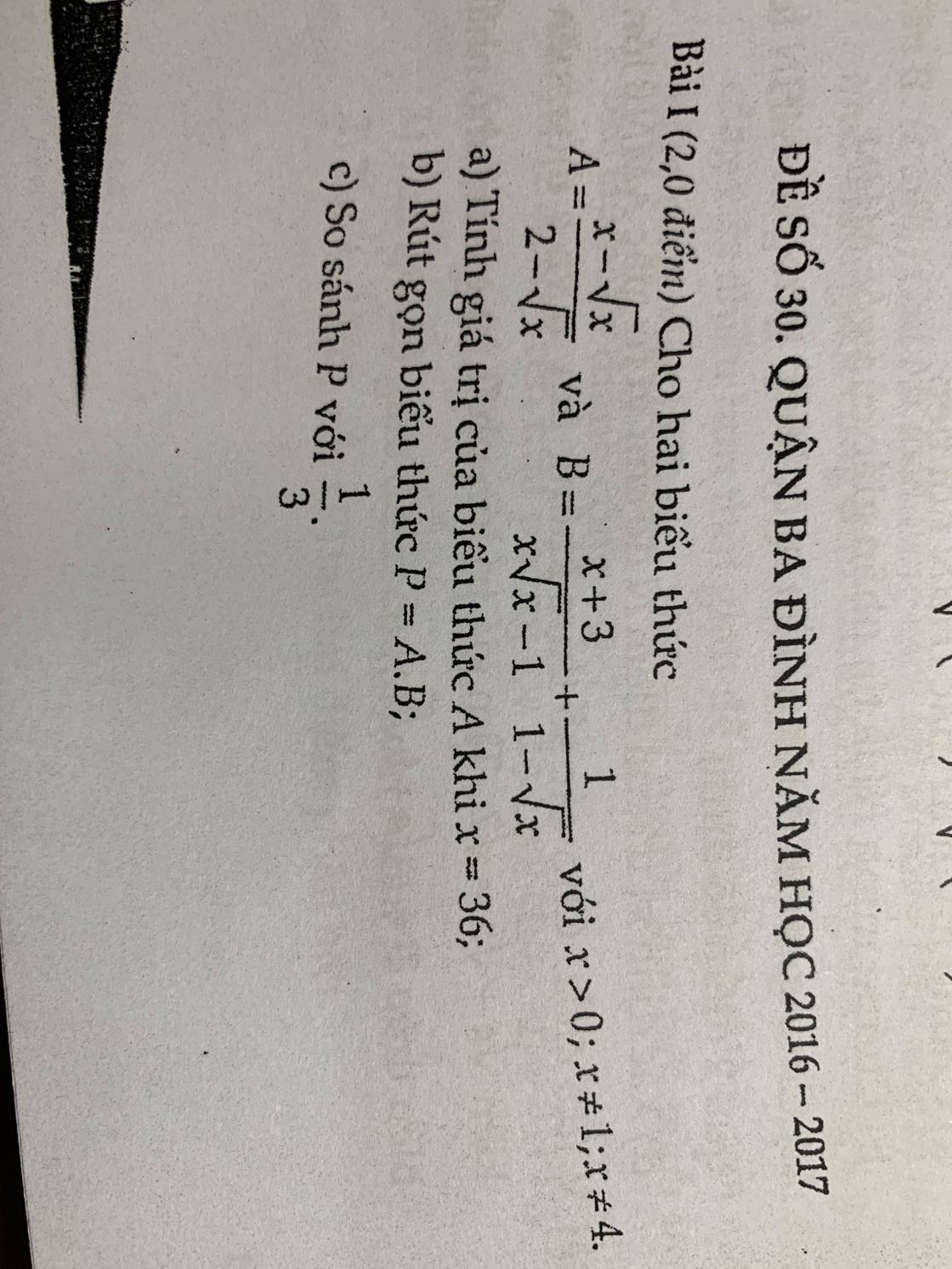




Câu 10: C
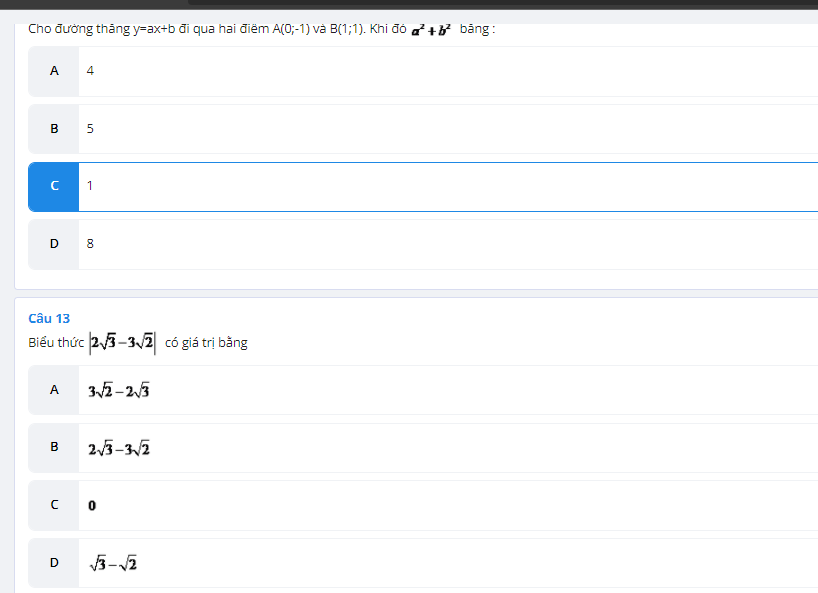
Câu 13: A
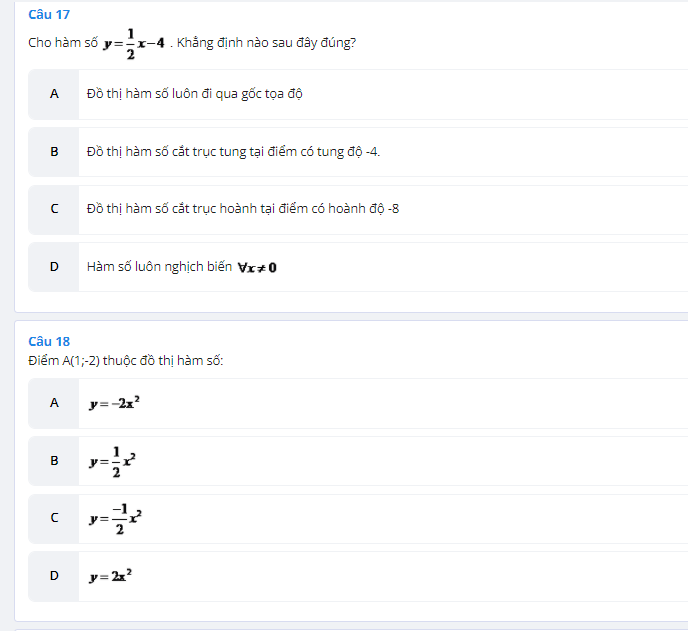
Câu 17:B
Câu 18: A
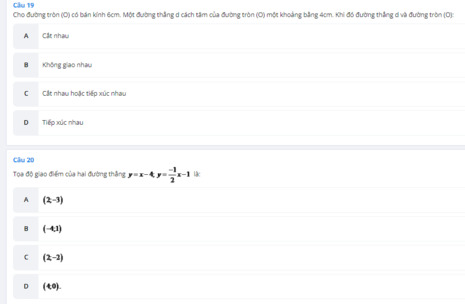
C
A
B
A