Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(=\dfrac{3}{7}\left(\dfrac{15}{13}-1-1\right)=\dfrac{3}{7}\cdot\dfrac{-11}{13}=-\dfrac{33}{91}\)

\(\dfrac{-1}{9}.\dfrac{-3}{5}+\dfrac{5}{-6}.\dfrac{-3}{5}-\dfrac{7}{2}.\dfrac{3}{5}\\=\dfrac{1}{9}.\dfrac{3}{5}+\dfrac{5}{6}.\dfrac{3}{5}-\dfrac{7}{2}.\dfrac{3}{5}\\ =\dfrac{3}{5}\left(\dfrac{1}{9}+\dfrac{5}{6}-\dfrac{7}{2}\right)\\ =\dfrac{3}{5}.\dfrac{-23}{9}\\ =-\dfrac{23}{15}\)

Để đánh số trang từ 1 đến 9 cần :
( 9 - 1 ) : 1 + 1 = 9 ( chữ số )
Để đánh số trang từ 10 đến 99 cần :
[ ( 99 - 10 ) : 1 + 1 ] x 2 = 180 ( chữ số )
Đế đánh số trang từ 100 đến 120 cần :
[ ( 120 - 100 ) : 1 + 1 ] x 3 = 63 ( chữ số )
Để đánh số trang từ 1 đến 120 cần :
9 + 180 + 63 = 252 ( chữ số )

1) ta có:\(2^{150}\)= (2^3)^50=8^50
\(3^{100}\)= (3^2)^50 = 9^50
vì 8^50 < 9^50 => \(2^{150}\)<\(3^{100}\)

`(15-x)+(x-12)=7-(-5+x)`
`=>15-x+x-12=7+5-x`
`=>3=12-x`
`=>x=12-3`
`=>x=9`
Vậy `x=9`

Ta có: Aabc =A.1000+abc
vì 1000 chia hết cho 125 và 8
nên tính chất của Aabc đối với 125 và 8
phụ thuộc vào ba số cuối abc
theo bài gia ta có
(abc-4) chia hết cho 125
=>(abc-4) có tận cùng là 5 hoặc 0
=> abc có tân cùng là 9 hoặc 4 (1)
(abc-7) chia hết cho 8
=> (abc-7) chẵn
=> abc lẻ (2)
Từ (1) và (2) suy ra c=9
ta có ab9-4=ab5=125.k (với 0<k<8)
Lại có ab9-7 chia hết cho 8
Suy ra ab5-3 chia hết cho 8
<=>125.k-3 chia hết cho 8
<=>(128k-3k-3) chia hết cho 8
<=>128k-3(k+1) chia hết cho 8
<=>3(k+1) chia hết cho 8 (vì 128k chia hết cho 8)
<=>k+1 chia hết cho 8 (vì 3 chia 3 dư 3)
<=>k=7 (vì 0<k<8)
Suy ra số cần tìm là 125.k+4=125.7+4=879
879 chia 1000 dư 879
Gọi số cần tìm là x.
Ta có:x chia cho 8 dư 7\(\Rightarrow\left(x+7\right)⋮8\Leftrightarrow x=8m+7\)
x chia cho 125 dư 4\(\Rightarrow\left(x+4\right)⋮125\Leftrightarrow x=125n+4\)
Vì x=x nên ta có \(8m+7=125n+4\)
\(8m+7=8n+117n+4\)
\(8\left(m-n\right)+7-4=117n\)
\(8\left(m-n\right)+3=117n\)
\(8\left(m-n\right)=\left(117n-3\right)\)
\(\left(117n-3\right)\inƯ\left(8\right)\)
Vì x nhỏ nhất nên ........
Ghép điều kiện vào rồi tính.
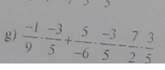

\(=\dfrac{1}{2}\left(\dfrac{2}{15}+\dfrac{2}{35}+\dfrac{2}{63}+\dfrac{2}{99}+\dfrac{2}{143}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{13}\right)\)
\(=\dfrac{1}{2}\cdot\dfrac{10}{39}=\dfrac{5}{39}\)
= 5/39