
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



5a.
$\frac{1}{2}-\sqrt{x}=0$
$\Rightarrow \sqrt{x}=\frac{1}{2}$
$\Rightarrow x=(\frac{1}{2})^2=\frac{1}{4}$
5b.
$\frac{5}{11}\sqrt{x}-\frac{1}{6}=\frac{1}{3}$
$\Rightarrow \frac{5}{11}\sqrt{x}=\frac{1}{3}+\frac{1}{6}=\frac{1}{2}$
$\Rightarrow \sqrt{x}=\frac{1}{2}: \frac{5}{11}=\frac{11}{10}$
$\Rightarrow x=(\frac{11}{10})^2=\frac{121}{100}$
5c.
$-\frac{4}{3}\sqrt{x}+\frac{8}{5}=\frac{1}{3}+\frac{2}{3}=1$
$\Rightarrow -\frac{4}{3}\sqrt{x}=1-\frac{8}{5}=\frac{-3}{5}$
$\Rightarrow \frac{4}{3}\sqrt{x}=\frac{3}{5}$
$\Rightarrow \sqrt{x}=\frac{3}{5}: \frac{4}{3}=\frac{9}{20}$
$\Rightarrow x=(\frac{9}{20})^2=\frac{81}{400}$
5d.
$x-6\sqrt{x}=0$
$\Rightarrow \sqrt{x}(\sqrt{x}-6)=0$
$\Rightarrow \sqrt{x}=0$ hoặc $\sqrt{x}-6=0$
$\Rightarrow \sqrt{x}=0$ hoặc $\sqrt{x}=6$
$\Rightarrow x=0$ hoặc $x=36$
5e.
$1-3x^2=7$
$3x^2=1-7=-6$
$x^2=-2<0$ (vô lý)
Do đđ không tồn tại $x$ thỏa mãn đề.
5f.
$7x^2-4=1$
$7x^2=1+4=5$
$x^2=\frac{5}{7}=(\sqrt{\frac{5}{7}})^2=(-\sqrt{\frac{5}{7}})^2$
$\Rightarrow x=\pm \sqrt{\frac{5}{7}}$

a: Xét ΔAMB và ΔAMC có
AB=AC
\(\widehat{BAM}=\widehat{CAM}\)
AM chung
Do đó: ΔAMB=ΔAMC
b: Ta có: ΔABC cân tại A
mà AM là đường phân giác
nên AM là đường trung trực của BC

`8,`
`a,`
`M(x)=A(x)+B(x)`
`M(x)=(x^3-3x^2+5x+3)+(-x^3+x^2+x^4-5x+3)`
`= x^3-3x^2+5x+3-x^3+x^2+x^4-5x+3`
`= x^4+ (x^3-x^3)+(-3x^2+x^2)+(5x-5x)+(3+3)`
`= x^4-2x^2+6`
`N(x)=A(x)-B(x)`
`N(x)=(x^3-3x^2+5x+3)-(-x^3+x^2+x^4-5x+3)`
`= x^3-3x^2+5x+3+x^3-x^2-x^4+5x-3`
`= x^4+(x^3+x^3)+(-3x^2-x^2)+(5x+5x)+(3-3)`
`= x^4+2x^3-4x^2+10x`
`b,`
Thay `x=1`
`M(1)=1^4-2*1^2+6=1-2+6=-1+6=5`
`-> x=1` không phải là nghiệm của đa thức.
`c,`
`M(x)=x^4-2x^2+6=0`
\(\text{Vì }\)\(x^4\ge0\text{ }\forall\text{ }x\)
`-> x^4-2x^2+6 >0 AA x`
`->` Đa thức vô nghiệm.
a)\(M\left(x\right)=x^3-3x^2+5x+3-x^3+4x^2+x^4-5x+3\\ =x^4+x^2+6\)
\(N\left(x\right)=x^3-3x^2+5x+3+x^3-4x^2-x^4+5x-3\\ =-x^4+2x^3-7x^2+10x\)
b) \(M\left(1\right)=1^4+1^2+6=8\ne0\)
=> x=1 ko phai la nghiem M(x)
c) De M(x) co nghiem
\(x^4+x^2+6=0\)
vi \(x^4\ge0\forall x\\ x^2\ge0\forall x\\ \Rightarrow x^4+x^2+6\ge6\)
=> vo nghiem

a: Xét tứ giác ACMD co
góc ACD=góc AMD=90 độ
=>ACMD là tứ giác nội tiếp
b: Xet ΔCHA vuông tại C và ΔCBD vuông tại C co
góc CAH=góc CDB
=>ΔCHA đồng dạng với ΔCBD
=>CH/CB=CA/CD
=>CH*CD=CA*CB
c: Xét ΔBAD có
AM,DC là đường cao
AM cắt DC tại H
=>H là trực tâm
=>BH vuông góc AD
mà BH vuông góc AH(H nằm trên đường tròn đường kính AB)
nên A,H,D thẳng hàng

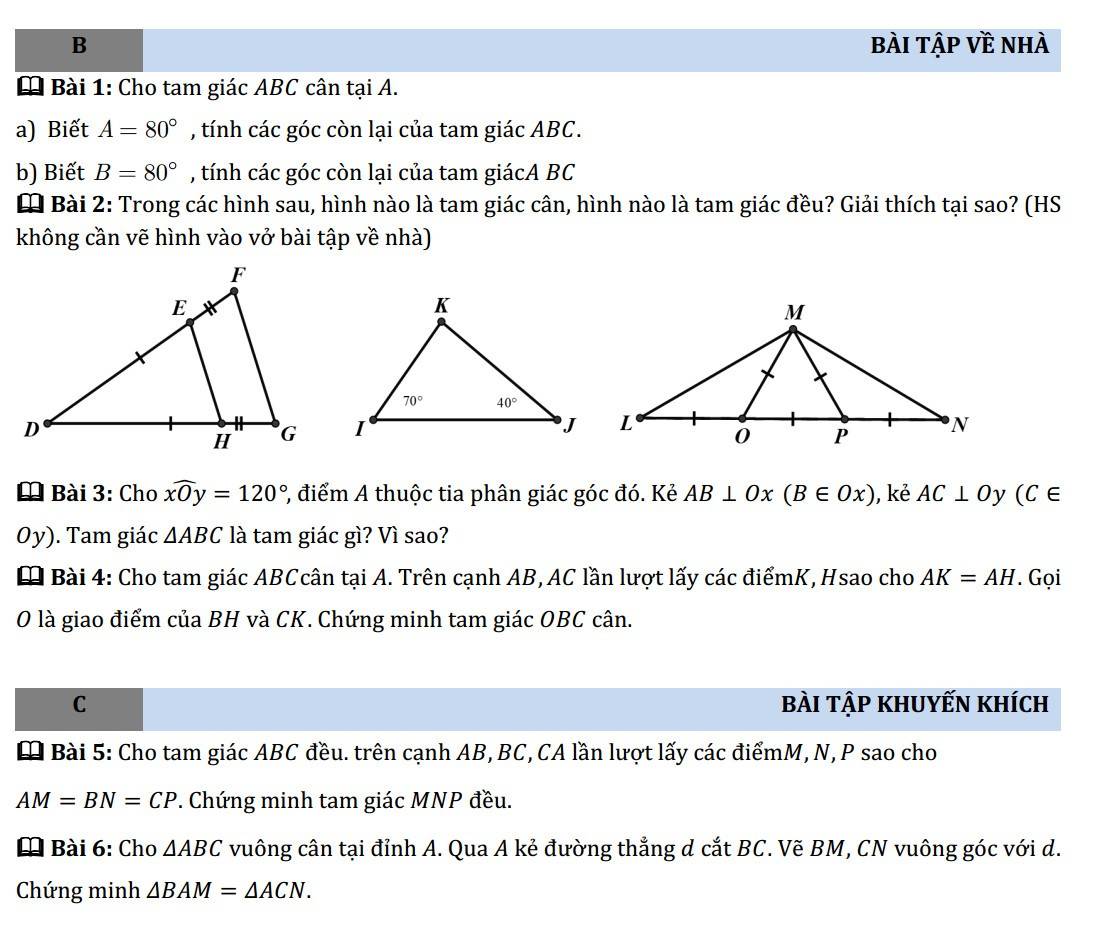
Bài 1
a) ∆ABC cân tại A
⇒ ∠B = ∠C = (180⁰ - ∠A) : 2
= (180⁰ - 80⁰) : 2
= 50⁰
Vậy ∠A = 80⁰; ∠B = ∠C = 50⁰
b) ∆ABC cân tại A
⇒ ∠C = ∠B = 80⁰
⇒ ∠A = 180⁰ - (∠B + ∠C)
= 180⁰ - (80⁰ + 80⁰)
= 20⁰
Vậy ∠A = 20⁰, ∠B = ∠C = 80⁰

Bài 11:
a) Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
Do đó: ΔBAD=ΔBED(Cạnh huyền-góc nhọn)
Suy ra: BA=BE(Hai cạnh tương ứng) và DA=DE(Hai cạnh tương ứng)
Ta có: BA=BE(cmt)
nên B nằm trên đường trung trực của AE(1)
Ta có: DA=DE(cmt)
nên D nằm trên đường trung trực của AE(2)
Từ (1) và (2) suy ra BD là đường trung trực của AE(đpcm)

\(a,\) Áp dụng t/c dtsbn:
\(\dfrac{x}{10}=\dfrac{y}{6}=\dfrac{z}{21}=\dfrac{5x}{50}=\dfrac{2z}{42}=\dfrac{5x+y-2z}{50+6-42}=\dfrac{28}{14}=2\\ \Rightarrow\left\{{}\begin{matrix}x=20\\y=12\\z=42\end{matrix}\right.\\ b,\dfrac{x}{3}=\dfrac{y}{4}\Rightarrow\dfrac{x}{15}=\dfrac{y}{20};\dfrac{y}{5}=\dfrac{z}{7}\Rightarrow\dfrac{y}{20}=\dfrac{z}{28}\\ \Rightarrow\dfrac{x}{15}=\dfrac{y}{20}=\dfrac{z}{28}\)
Áp dụng t/c dtsbn
\(\dfrac{x}{15}=\dfrac{y}{20}=\dfrac{z}{28}=\dfrac{2x}{30}=\dfrac{3y}{60}=\dfrac{2x+3y-z}{30+60-28}=\dfrac{124}{62}=2\\ \Rightarrow\left\{{}\begin{matrix}x=30\\y=40\\z=56\end{matrix}\right.\)
\(c,\) Áp dụng t/c dtsbn
\(\dfrac{2x}{3}=\dfrac{3y}{4}=\dfrac{4z}{5}=\dfrac{x}{\dfrac{3}{2}}=\dfrac{y}{\dfrac{4}{3}}=\dfrac{z}{\dfrac{5}{4}}=\dfrac{x+y+z}{\dfrac{3}{2}+\dfrac{4}{3}+\dfrac{5}{4}}=\dfrac{49}{\dfrac{49}{12}}=12\\ \Rightarrow\left\{{}\begin{matrix}x=12\cdot\dfrac{3}{2}=18\\y=12\cdot\dfrac{4}{3}=16\\z=12\cdot\dfrac{5}{4}=15\end{matrix}\right.\)
\(d,\) Đặt \(\dfrac{x}{2}=\dfrac{y}{3}=k\Rightarrow x=2k;y=3k\)
\(xy=54\Rightarrow2k\cdot3k=54\Rightarrow k^2=9\Rightarrow\left[{}\begin{matrix}k=3\\k=-3\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=6;y=9\\x=-6;y=-9\end{matrix}\right.\)
\(e,\) Đặt \(\dfrac{x}{5}=\dfrac{y}{3}=k\Rightarrow x=5k;y=3k\)
\(x^2-y^2=4\Rightarrow25k^2-9k^2=4\Rightarrow16k^2=4\Rightarrow k^2=\dfrac{1}{4}\\ \Rightarrow\left[{}\begin{matrix}k=\dfrac{1}{2}\\k=-\dfrac{1}{2}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{5}{2};y=\dfrac{3}{2}\\x=-\dfrac{5}{2};y=-\dfrac{3}{2}\end{matrix}\right.\)
\(f,\) Áp dụng t/c dtsbn:
\(\dfrac{x}{y+z+1}=\dfrac{y}{z+x+1}=\dfrac{z}{x+y-2}=\dfrac{x+y+z}{2\left(x+y+z\right)}=\dfrac{1}{2}=x+y+z\)
\(\Rightarrow\left\{{}\begin{matrix}2x=y+z+1\\2y=x+z+1\\2z=x+y-2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x+y+z=3x-1\\x+y+z=3y-1\\x+y+z=3z+2\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}3x-1=\dfrac{1}{2}\\3y-1=\dfrac{1}{2}\\3z+2=\dfrac{1}{2}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{1}{2}\\z=-\dfrac{1}{2}\end{matrix}\right.\)
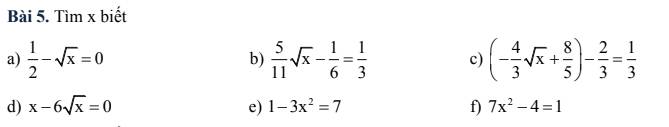

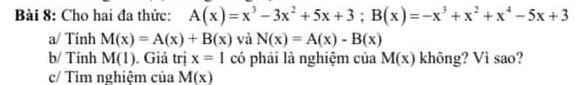 giúp mik với ạ, mik đang cần gấp><
giúp mik với ạ, mik đang cần gấp><



Lời giải:
$\frac{b}{2}=\frac{c}{5}\Leftrightarrow \frac{b}{4}=\frac{c}{10}$
Vậy: $\frac{a}{3}=\frac{b}{4}=\frac{c}{10}$
Áp dụng tính chất dãy tỉ số bằng nhau:
$\frac{a}{3}=\frac{b}{4}=\frac{c}{10}=\frac{a+b-c}{3+4-10}=\frac{3}{-3}=-1$
$\Rightarrow a=-1.3=-3; b=-1.4=-4; c=-1.10=-10$
em cảm ơn ạ