K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
3 tháng 8 2018
\(x^2+4y^2-4x-4y+5=0\)
\(\Leftrightarrow\left(x^2-4x+4\right)+\left(4y^2-4y+1\right)=0\)
\(\Leftrightarrow\left(x-2\right)^2+\left(2y-1\right)^2=0\)
\(\Leftrightarrow\hept{\begin{cases}\left(x-2\right)^2=0\\\left(2y-1\right)^2=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=2\\y=\frac{1}{2}\end{cases}}\)
TN
3 tháng 8 2018
\(x^2+4y^2-4x-4y+5=0\)
<=> \(\left(x^2-4x+4\right)+\left(4y^2-4y+1\right)=0\)
<=> \(\left(x-2\right)^2+\left(2y-1\right)^2=0\)
<=> \(\hept{\begin{cases}x-2=0\\2y-1=0\end{cases}}\)
<=> \(\hept{\begin{cases}x=2\\y=\frac{1}{2}\end{cases}}\)
học tốt
DT
16 tháng 12 2021
a, Xét tam giác ABC có AD=DB,AE=EC
=>DE là đường trung bình của tam giác ABC
b,Xét tứ giác DQBC có :
DE//BC=>DQ//BC(E nằm trên đường thẳng DQ)
DQ=BC(gt)
=>tứ giác DQBC là hình bình hành
c, Xét tứ giác AKCH có:
AE=AC(gt)
HE=EK(gt)
=>tứ giác AKCH là hình chữ nhật
9 tháng 7 2018
nhưng đây là toán 8 ,đầu năm thì đc hok hằng đẳng thức nên sẽ áp dụng theo HĐT
9 tháng 7 2018
đề e đăng sai rồi,sửa:
\(\left(2x+1\right)\left(4x^2-2x+1\right)-\left(8x^3-1\right)\)
\(=8x^3+1-8x^3+1\)
\(=2\)
Vậy gt bt trên ko phụ thuộc vào biến.
DD
1
SA
2 tháng 8 2018
Mình lười ko chép lại đề nhé ( thông cảm )
a, 3x . x + 3x . (-4) - 2x + 8 = 0
3x2 - 12x - 2x + 8 = 0
3x2 - 14x = - 8
Đến đoạn này bn thu x về một vế và tính nha ( tịt mợ r)
b, ( 3x)2 - 2.3x.1 + 12 - " đoạn này phải là ( 3x - 1 ).(3x+1) chứ" (3x)2 - 12 = 2
9x2 - 6x +1 - 9x2 - 1 = 2
- 6x = 2
x = 2 / -6
x = -1/3
Mh chỉ giúp đc ngần vầy , sai đừng ai anti nhá , mơn nhìu !!! Mh là FAN KPOP chính hiệu , kb nhoa mn
~ HOK TỐT ~
DD
2
30 tháng 7 2018
\(a,x^2+y^2-4x-2y+6\)
\(=\left(x^2-4x+4\right)+\left(y^2-2y+1\right)+1\)
\(=\left(x-2\right)^2+\left(y-1\right)^2+1\)
Ta có: \(\left(x-2\right)^2+\left(y-1\right)^2\ge0\forall x,y\)
\(\Rightarrow\left(x-2\right)^2+\left(y-1\right)^2+1\ge1\forall x,y\)
Hay: \(x^2+y^2-4x-2y+6\ge1\)
\(b,x^2+4y^2+z^2-4x+4y-8z+25\)
\(=\left(x^2-4x+4\right)+\left(4y^2+4y+1\right)+\left(z^2-8z+16\right)+4\)
\(=\left(x-2\right)^2+\left(2y+1\right)^2+\left(z-4\right)^2+4\)
Vì: \(\left(x-2\right)^2+\left(2y+1\right)^2+\left(z-4\right)^2\ge0\forall x,y,z\)
\(\Rightarrow\left(x-2\right)^2+\left(2y+1\right)^2+\left(z-4\right)^2+4\ge4\forall x,y,z\)
Hay: \(x^2+4y^2+z^2-4x+4y-8z+25\ge4\)
=.= hok tốt !!
NV
1
10 tháng 10 2021
\(P=\dfrac{x^3-y^3}{x^2y-xy^2}-\dfrac{x^3+y^3}{x^2y+xy^2}-\left(\dfrac{x}{y}-\dfrac{y}{x}\right)\left(\dfrac{x+y}{x-y}-\dfrac{x-y}{x+y}\right)\)
\(=\dfrac{\left(x-y\right)\left(x^2+xy+y^2\right)}{xy\left(x-y\right)}-\dfrac{\left(x+y\right)\left(x^2-xy+y^2\right)}{xy\left(x+y\right)}-\dfrac{x^2-y^2}{xy}\cdot\dfrac{x^2+2xy+y^2-x^2+2xy-y^2}{\left(x-y\right)\left(x+y\right)}\)
\(=\dfrac{x^2+xy+y^2-x^2+xy-y^2}{xy}-\dfrac{\left(x-y\right)\left(x+y\right)}{xy}\cdot\dfrac{4xy}{\left(x-y\right)\left(x+y\right)}\)
\(=2-4=-2\)
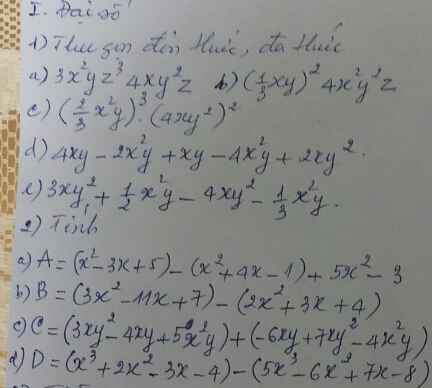
Bài 2:
a: Ta có: \(A=\left(x^2-3x+5\right)-\left(x^2+4x-1\right)+5x^2-3\)
\(=x^2-3x+5-x^2-4x+1+5x^2-3\)
\(=5x^2-7x+3\)
b: Ta có: \(B=\left(3x^2-11x+7\right)-\left(2x^2+3x+4\right)\)
\(=3x^2-11x+7-2x^2-3x-4\)
\(=x^2-14x+3\)