K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HP
21 tháng 10 2021
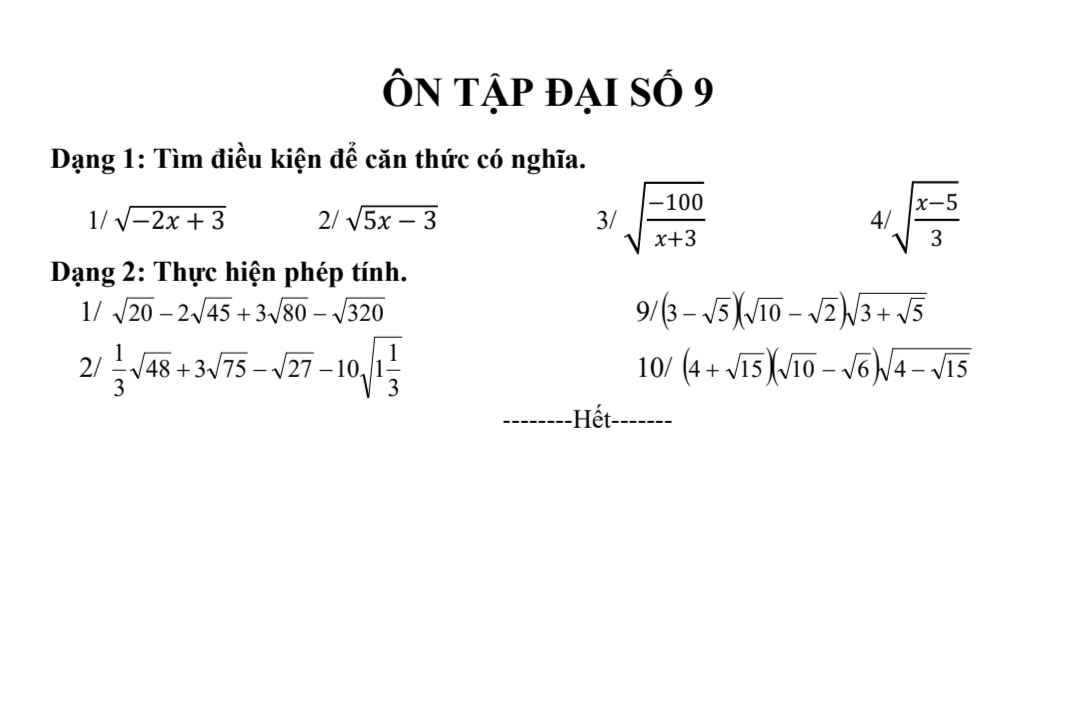
Dạng 1:
1/ ĐKXĐ: \(x\le0\)
2/ ĐKXĐ: \(x\ge\dfrac{3}{5}\)
3/ ĐKXĐ: \(x\le-4\)
4/ ĐKXĐ: \(x\ge5\)
21 tháng 10 2021
Dạng 1:
\(1,ĐK:-2x+3\ge0\Leftrightarrow x\le\dfrac{3}{2}\\ 2,ĐK:5x-3\ge0\Leftrightarrow x\ge\dfrac{3}{5}\\ 3,ĐK:\dfrac{-100}{x+3}\ge0\Leftrightarrow x+3< 0\left(-100< 0;x+3\ne0\right)\\ \Leftrightarrow x< -3\\ 4,ĐK:\dfrac{x-5}{3}\ge0\Leftrightarrow x-5\ge0\left(3>0\right)\\ \Leftrightarrow x\ge5\)
Dạng 2:
\(1,=2\sqrt{5}-6\sqrt{5}+12\sqrt{5}-8\sqrt{5}=0\\ 9,=\left(3-\sqrt{5}\right)\left(\sqrt{5}-1\right)\sqrt{6+2\sqrt{5}}\\ =\left(3-\sqrt{5}\right)\left(\sqrt{5}-1\right)\left(\sqrt{5}+1\right)\\ =4\left(3-\sqrt{5}\right)=12-4\sqrt{5}\\ 2,=\dfrac{4\sqrt{3}}{3}+15\sqrt{3}-3\sqrt{3}-\dfrac{20\sqrt{3}}{3}\\ =12\sqrt{3}-\dfrac{16\sqrt{3}}{3}=\dfrac{36\sqrt{3}-16\sqrt{3}}{3}=\dfrac{20\sqrt{3}}{3}\\ 10,=\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\sqrt{8-2\sqrt{15}}\\ =\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}-\sqrt{3}\right)\\ =\left(4+\sqrt{15}\right)\left(8-2\sqrt{15}\right)\\ =32-8\sqrt{15}+8\sqrt{15}-30=2\)
7 tháng 7 2021
1) ĐKXĐ: \(x\ge0\)
2) ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne9\end{matrix}\right.\)
3) ĐKXĐ: \(x\ge4\)
4) ĐKXĐ: \(x>16\)
5) ĐKXĐ: \(\left[{}\begin{matrix}x\le-2\\x\ge0\end{matrix}\right.\)
6) ĐKXĐ: \(\left[{}\begin{matrix}x\le-1\\x\ge4\end{matrix}\right.\)
7) ĐKXĐ: \(\left[{}\begin{matrix}1\le x\\x< 3\end{matrix}\right.\)
7 tháng 7 2021
8) ĐKXĐ: \(\left[{}\begin{matrix}x\le-2\\x>3\end{matrix}\right.\)
9) ĐKXĐ: \(x\in R\)
10) ĐKXĐ: \(x\in R\)
11) ĐKXĐ: \(x\in R\)
12) ĐKXĐ: \(x\in R\)
13) ĐKXĐ: \(x\in R\)
14) ĐKXĐ: \(x\in R\)
15) ĐKXĐ: \(x\in R\)
16) ĐKXĐ: \(x\ne-\dfrac{1}{2}\)
17) ĐKXĐ: \(x\ge7\)
18) ĐKXĐ: \(x\ge-5\)
NT
2
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 7 2021
1.
Xét pt đầu:
\(x^2-xy+x-y=0\)
\(\Leftrightarrow x\left(x-y\right)+x-y=0\)
\(\Leftrightarrow\left(x+1\right)\left(x-y\right)=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=y\end{matrix}\right.\)
TH1: \(x=-1\) thay xuống pt dươi:
\(\sqrt{y^2+15}=-3-2+\sqrt{9}\Leftrightarrow\sqrt{y^2+15}=-2< 0\) (vô nghiệm)
TH2: thay \(y=x\) xuống pt dưới:
\(\sqrt{x^2+15}=3x-2+\sqrt{x^2+8}\) (1)
\(\Rightarrow3x-2=\sqrt{x^2+15}-\sqrt{x^2+8}=\dfrac{7}{\sqrt{x^2+15}+\sqrt{x^2+8}}>0\)
\(\Rightarrow x>\dfrac{2}{3}\)
Do đó (1) tương đương:
\(3x-2+\sqrt{x^2+8}-\sqrt{x^2+15}=0\)
\(\Leftrightarrow3x-3+\sqrt{x^2+8}-3+4-\sqrt{x^2+15}=0\)
\(\Leftrightarrow3\left(x-1\right)+\dfrac{\left(x-1\right)\left(x+1\right)}{\sqrt{x^2+8}+3}-\dfrac{\left(x-1\right)\left(x+1\right)}{\sqrt{x^2+15}+4}=0\)
\(\Leftrightarrow\left(x-1\right)\left[3+\left(x+1\right)\left(\dfrac{1}{\sqrt{x^2+8}+3}-\dfrac{1}{\sqrt{x^2+15}+4}\right)\right]=0\)
\(\Leftrightarrow x-1=0\) (do \(x+1>0\) nên ngoặc phía sau luôn dương)
\(\Leftrightarrow x=y=1\)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 7 2021
2.
Pt đầu tương đương:
\(y^2-x+x^2-2xy+x=0\)
\(\Leftrightarrow\left(x-y\right)^2=0\Leftrightarrow y=x\)
Thay xuống pt dưới:
\(2x^2+x-x^2+x-3=0\)
\(\Leftrightarrow x^2+2x-3=0\)
\(\Rightarrow\left[{}\begin{matrix}x=1\Rightarrow y=1\\x=-3\Rightarrow y=-3\end{matrix}\right.\)
18 tháng 10 2021
Bài III:
1: Ta có: \(\sqrt{x-3}=5\)
\(\Leftrightarrow x-3=25\)
hay x=28
2: Ta có: \(\dfrac{\sqrt{x}-2}{\sqrt{x}-5}=\dfrac{1}{3}\)
\(\Leftrightarrow3\sqrt{x}-6=\sqrt{x}-5\)
\(\Leftrightarrow2\sqrt{x}=1\)
hay \(x=\dfrac{1}{4}\)
NL
1
17 tháng 10 2021
Bài 7:
a: \(A=x+\sqrt{x}\ge0\forall x\)
Dấu '=' xảy ra khi x=0
NQ
0
