
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Khá dễ dàng nhận ra do tính chất đường trung bình nên tam giác \(A_1B_1C_1\) chia tam giác ABC thành 4 tam giác có diện tích bằng nhau
\(\Rightarrow S_{A_1B_1C_1}=\dfrac{1}{4}S_{ABC}\)
Do đó \(S_1;S_2...;S_{50}\) lập thành 1 cấp số nhân với \(u_1=S_1=\dfrac{6}{4}=\dfrac{3}{2}\) và \(q=\dfrac{1}{4}\)
\(\Rightarrow S\left(50\right)=\dfrac{3}{2}.\dfrac{1-\left(\dfrac{1}{4}\right)^{50}}{1-\dfrac{1}{4}}\)


\(\lim\limits_{x\rightarrow3}\left(\dfrac{1}{x}-\dfrac{1}{3}\right)\dfrac{1}{\left(x-3\right)^3}=\lim\limits_{x\rightarrow3}\dfrac{1}{3x\left(x-3\right)^2}=+\infty\)

Gọi số học sinh nam là a (18<a<36)
Số học sinh nam biết bơi là b, số học sinh nữ biết bơi là c (lẻ)
\(\Rightarrow\dfrac{C_b^1.C_c^1}{C_a^1.C_{36-a}^1}=\dfrac{140}{299}\)
\(\Rightarrow299bc=140a\left(36-a\right)\)
Do \(a+36-a=36\) chẵn \(\Rightarrow\) a và \(36-a\) cùng tính chẵn lẻ
Mặt khác 299 và 140 nguyên tố cùng nhau \(\Rightarrow a\left(36-a\right)⋮299\left(=13.23\right)\)
Do 18<a<36 \(\Rightarrow\) mỗi số a và 36-a không thể đồng thời chia hết 13 và 23
\(\Rightarrow\) a chia hết cho 13 hoặc 23
TH1: \(a⋮13\Rightarrow a=26\Rightarrow36-a=10\) không chia hết 23 (loại)
TH2: \(a⋮23\Rightarrow a=23\Rightarrow36-a=13\) (thỏa mãn)
\(\Rightarrow bc=140\left(=4.5.7\right)\)
Do c lẻ, và \(c< 36-a=13\), đồng thời \(b< a=23\)
TH1: \(c=5\Rightarrow b=28>a\left(ktm\right)\)
TH2: \(c=7\Rightarrow b=20\) (thỏa mãn)
Vậy có 20 học sinh nam biết bơi



Do vai trò của 3 biến là như nhau, không mất tính tổng quát giả sử \(x>y>z\)
Ta có: \(x-z=\left(x-y\right)+\left(y-z\right)\)
Đặt \(\left\{{}\begin{matrix}x-y=a>0\\y-z=b>0\end{matrix}\right.\)
Do \(x;z\in\left[0;2\right]\Rightarrow x-z\le2\) hay \(a+b\le2\)
Ta có:
\(P=\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{\left(a+b\right)^2}\ge\dfrac{1}{2}\left(\dfrac{1}{a}+\dfrac{1}{b}\right)^2+\dfrac{1}{\left(a+b\right)^2}\ge\dfrac{1}{2}\left(\dfrac{4}{a+b}\right)^2+\dfrac{1}{\left(a+b\right)^2}\)
\(P\ge\dfrac{9}{\left(a+b\right)^2}\ge\dfrac{9}{2^2}=\dfrac{9}{4}\)
Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}a=b\\a+b=2\\\end{matrix}\right.\) \(\Rightarrow a=b=1\) hay \(\left(x;y;z\right)=\left(0;1;2\right)\) và các hoán vị

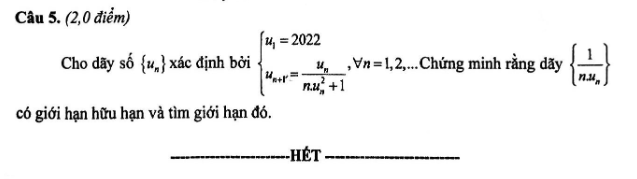
\(\dfrac{1}{u_{n+1}}=\dfrac{1}{u_n}+nu_n\)
Đặt \(v_n=\dfrac{1}{u_n}\Rightarrow\left\{{}\begin{matrix}v_1=\dfrac{1}{2022}\\v_{n+1}=v_n+\dfrac{n}{v_n}\end{matrix}\right.\) và \(\left\{\dfrac{1}{nu_n}\right\}=\left\{\dfrac{v_n}{n}\right\}\)
Ta sẽ chứng minh \(v_n\ge n\) với \(n>1\)
Với \(n=2\Rightarrow v_2=v_1+2022>2\) (đúng)
Giả sử điều đó đúng với \(n=k>1\) hay \(v_k\ge k\)
Ta cần chứng minh \(v_{k+1}\ge k+1\)
Thật vậy, do \(v_k\ge k\), đặt \(v_k=k+\alpha\) với \(\alpha\ge0\)
Khi đó: \(v_{k+1}=v_k+\dfrac{k}{v_k}=k+\alpha+\dfrac{k}{k+\alpha}=k+\dfrac{k\alpha+\alpha^2+k}{k+\alpha}\ge k+\dfrac{\alpha+k}{k+\alpha}=k+1\) (đpcm)
Tương tự, ta quy nạp chứng minh được \(v_n\le n+v_2\) với \(n>1\) (do \(v_2\) số xấu nên ko ghi)
Kiểm tra với \(n=2\Rightarrow v_2\le2+v_2\) (đúng)
Giả sử \(v_k\le k+v_2\)
\(\Rightarrow v_{k+1}=v_k+\dfrac{k}{v_k}\le k+v_2+\dfrac{k}{v_k}\le k+v_2+\dfrac{k}{k}=k+1+v_2\) (đpcm)
\(\Rightarrow n\le v_n\le n+v_2\) \(\Rightarrow1\le\dfrac{v_n}{n}\le\dfrac{n+v_2}{n}\)
Sử dụng định lý kẹp, dễ dàng suy ra \(\lim\left\{\dfrac{v_n}{n}\right\}=1\)

Kẻ \(HE\perp AD\) , do tam giác ABD đều \(\Rightarrow HE=\dfrac{a\sqrt{3}}{2}\) ; \(AE=\dfrac{1}{4}AD\)
\(\Rightarrow AE=BM\Rightarrow\) tứ giác AEBM là hình bình hành \(\Rightarrow\) H đồng thời là trung điểm ME
Kẻ \(HK\perp SE\Rightarrow HK\perp\left(SAD\right)\)
a. Ta có: \(SH=HE\Rightarrow\) tam giác SHE vuông cân tại H
\(\Rightarrow\) K đồng thời là trung điểm SE
\(\Rightarrow\) KH là đường trung bình tam giác SME \(\Rightarrow SM||HK\)
\(\Rightarrow SM\perp\left(SAD\right)\)
b. Từ C kẻ \(CX\perp\left(SAD\right)\Rightarrow\widehat{CSX}\) là góc giữa SC và (SAD) đồng thời \(CX=d\left(C;\left(SAD\right)\right)\)
\(\Rightarrow sin\alpha=sin\widehat{CSX}=\dfrac{CX}{SC}\)
Từ M kẻ \(MI\perp SE\Rightarrow MI||HK\Rightarrow MI\perp\left(SAD\right)\)
\(\Rightarrow MI=d\left(M;\left(SAD\right)\right)\)
Mà \(CM||AD\Rightarrow CM||\left(SAD\right)\Rightarrow d\left(C;\left(SAD\right)\right)=d\left(M;\left(SAD\right)\right)\)
\(\Rightarrow CX=MI\)
HK là đường trung bình tam giác MIE \(\Rightarrow MI=2HK\)
\(MI=2HK=\dfrac{2SH.HE}{\sqrt{SH^2+HE^2}}=\dfrac{SH.a\sqrt{3}}{\sqrt{SH^2+\dfrac{3a^2}{4}}}\)
\(SC=\sqrt{SH^2+CH^2}=\sqrt{SH^2+MH^2+CM^2}=\sqrt{SH^2+HE^2+CM^2}\)
\(=\sqrt{SH^2+7a^2}\)
\(\Rightarrow sin\alpha=\dfrac{SH.a\sqrt{3}}{\sqrt{SH^2+7a^2}.\sqrt{SH^2+\dfrac{3a^2}{4}}}=\dfrac{a\sqrt{3}}{\sqrt{SH^2+\dfrac{21a^4}{4SH^2}+\dfrac{31}{4}a^2}}\le\dfrac{a\sqrt{3}}{\sqrt{2\sqrt{\dfrac{21a^4}{4}}+\dfrac{31}{4}a^2}}\)
Dấu "=" xảy ra khi \(SH^2=\dfrac{21a^4}{4SH^2}\Rightarrow SH=a\sqrt[4]{\dfrac{21}{4}}\)
Em kiểm tra lại tính toán
 giúp em với ạ em cảm ơn nhiều lắm
giúp em với ạ em cảm ơn nhiều lắm


 mọi người giúp em với em cảm ơn nhiều lắm
mọi người giúp em với em cảm ơn nhiều lắm






 giúp em với em cảm ơn nhiều ạ
giúp em với em cảm ơn nhiều ạ giúp em với em cảm ơn nhiều lắmmm ạ
giúp em với em cảm ơn nhiều lắmmm ạ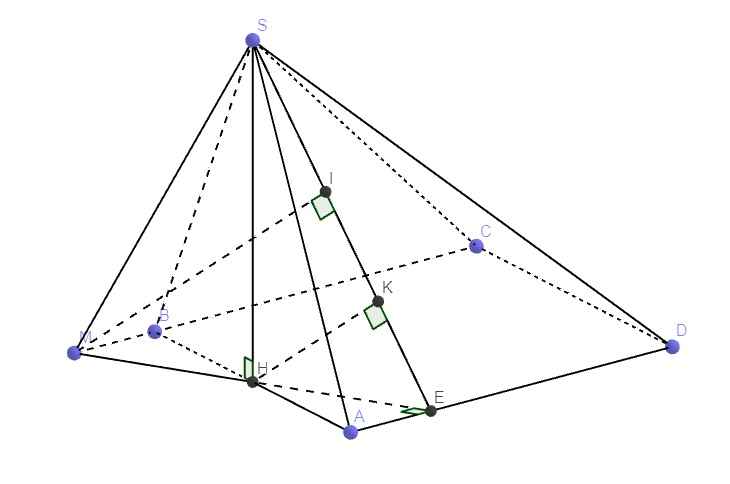
bài này mình gọi cttq Un=an^3+bn^2+cn+d. Khi thay n=1 thì = 6, n=2 thi Un=-4... đúng ko ạ
Hướng giải đó đúng rồi đấy, với dãy số thì cách đơn giản nhất là đưa về đa thức (chắc người ra đề cũng nghĩ vậy nên kết quả khá đẹp: a=-1, b=2, c=-1, d=6