
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
a) Xét ΔNMQ và ΔNEQ có
NM=NE(gt)
\(\widehat{MNQ}=\widehat{ENQ}\)
NQ chung
Do đó: ΔNMQ=ΔNEQ(c-g-c)
Suy ra: QM=QE(hai cạnh tương ứng)
Bài 1:
b) Ta có: ΔNMQ=ΔNEQ(cmt)
nên \(\widehat{NMQ}=\widehat{NEQ}\)(hai góc tương ứng)
hay \(\widehat{NEQ}=90^0\)

Mình không nhìn thấy câu hỏi, giờ mới thấy bạn ạ
Do mở rộng cạnh của thửa đất về cả bốn phía nên thửa đất mới sau khi mở rộng cũng là hình vuông. mỗi cạnh của thửa đất lúc sau đã tăng :
0,5 x 2 = 1 (m)
Gọi cạnh hình vuông lúc đầu là x đk x > 0
Thì cạnh hình vuông lúc sau là : x + 1
theo bài ra ta có : (x + 1)( x + 1) - x2 = 20
x2 + x + x + 1 - x2 = 20
2x = 20 -1
2x = 19
x = 19: 2
x = 9,5
Kết luận cạnh hình vuông lúc đầu là 9,5 m


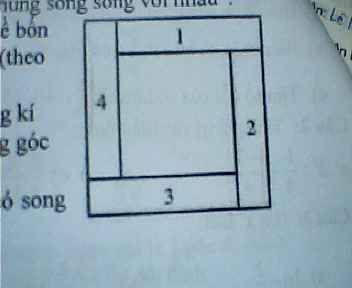
Bài 4:
Xét tứ giác ABCD có
M là trung điểm của AC
M là trung điểm của BD
Do đó:ABCD là hình bình hành
Suy ra: AD//BC
Xét tứ giác AEBC có
M là trung điểm của AB
M là trung điểm của EC
Do đó: AEBC là hình bình hành
Suy ra: AE//CB
mà AD//BC
và AE,AD có điểm chung là A
nên E,A,D thẳng hàng


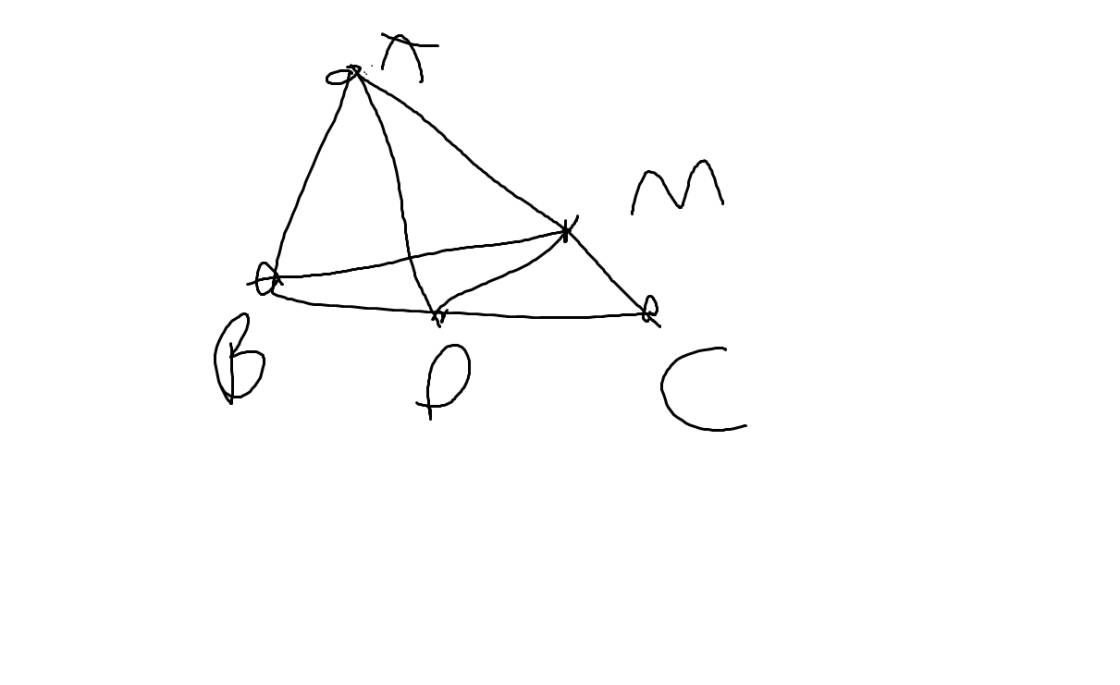
a: Xét ΔABD và ΔAMD có
AB=AM
\(\widehat{BAD}=\widehat{MAD}\)
AD chung
Do đó: ΔABD=ΔAMD
b: Ta có: ΔABD=ΔAMD
=>DB=DM
=>ΔDBM cân tại D
c: Ta có: AB=AM
=>A nằm trên đường trung trực của BM(1)
Ta có: DB=DM
=>D nằm trên đường trung trực của BM(2)
Từ (1) và (2) suy ra AD là đường trung trực của BM







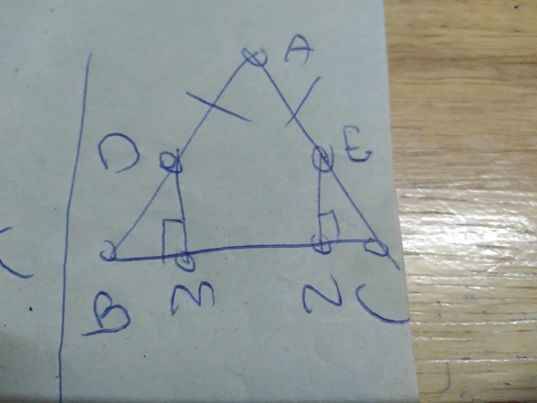

a: Xét ΔBAM và ΔBDM có
BA=BD
\(\widehat{ABM}=\widehat{DBM}\)
BM chung
Do đó: ΔBAM=ΔBDM
Suy ra: \(\widehat{BAM}=\widehat{BDM}=90^0\)
hay MD\(\perp\)BC
b: Xét ΔMAH vuông tại A và ΔMDC vuông tại D có
MA=MD
\(\widehat{AMH}=\widehat{DMC}\)
Do đó: ΔMAH=ΔMDC
c: Ta có: ΔBAM=ΔBDM
nên MA=MD
mà MD<MC
nên MA<MC
d: Ta có: BH=BC
nên B nằm trên đường trung trực của CH(1)
Ta có; MH=MC
nên M nằm trên đường trung trực của CH(2)
Ta có: KH=KC
nên K nằm trên đường trung trực của CH(3)
Từ (1), (2) và (3) suy ra B,M,K thẳng hàng
ko đc nói tục ở đây nhé bn