
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





a)
a/ Xét ΔABC và ΔDEC ta có:
\(\widehat{C}\) \(chung\)
\(\widehat{ABC}=\widehat{DEC}\left(gt\right)\)
\(\Rightarrow\Delta ABC\) ∼ \(\Delta DEC\left(g.g\right)\)
b/ \(Vì\) \(\Delta ABC\) ∼\(\Delta DEC\left(g.g\right)\left(cmt\right)\)
\(\Rightarrow\dfrac{AB}{DE}=\dfrac{AC}{DC}\)
b)
a/\(Xét\Delta ABE\) \(và\) \(\Delta KBH\) \(ta\) \(có:\)
\(\widehat{BEA}=\widehat{KHB}\left(gt\right)\)
\(\widehat{HBK}=\widehat{EBA}\left(đđ\right)\)
\(\Rightarrow\Delta ABE\)∼\(\Delta KBH\left(g.g\right)\)
b/ \(Vì\) \(\Delta ABE\)∼\(\Delta KBH\left(g.g\right)\left(cmt\right)\)
\(\rightarrow\dfrac{AE}{KH}=\dfrac{AB}{KB}\)
\(\Rightarrow AE.KB=KH.AB\)
c)
a/\(Xét\) \(\Delta AHQ\) \(và\) \(\Delta FEQ\) \(ta\) \(có\):
\(\widehat{Q}\) \(chung\)
\(\widehat{HAQ}=\widehat{EFQ}=90^0\)
\(\Rightarrow\Delta AHQ\)∼\(\Delta FEQ\left(g.g\right)\)
b/ \(Vì\) \(\Delta AHQ\)∼\(\Delta FEQ\left(g.g\right)\left(cmt\right)\)
\(\rightarrow\dfrac{AH}{EF}=\dfrac{HQ}{EQ}\)
\(\Rightarrow AH.EQ=EF.HQ\)
d)
a/\(Xét\Delta DEF\) \(và\) \(\Delta DAE\) \(ta\) \(có:\)
\(\widehat{D}\) \(chung\)
\(\widehat{DEF}=\widehat{EAD}=90^0\)
\(\Rightarrow\Delta DEF\)∼\(\Delta DAE\left(g.g\right)\left(1\right)\)
b/\(Xét\Delta EAF\) \(và\) \(\Delta FED\) \(ta\) \(có\):
\(\widehat{F}\) \(chung\)
\(\widehat{EAF}=\widehat{DEF}=90^0\)
\(\Rightarrow\Delta EAF\)∼\(\Delta FED\left(g.g\right)\left(2\right)\)
\(Từ\left(1\right)và\left(2\right)suy\) \(ra\) \(\Delta DEF\)∼\(\Delta DAE\)∼\(\Delta AEF\)
\(\Rightarrow\Delta DAE\)∼\(\Delta EAF\)
c/\(Vì\Delta DAE\)∼\(\Delta EAF\left(cmt\right)\)
\(\rightarrow\dfrac{EA}{DA}=\dfrac{AF}{EA}\)
\(\rightarrow EA.EA=DA.AF\)
\(\Rightarrow EA^2=DA.AF\)

a. Áp dụng định lí Py-ta-go vào tam giác ABC vuông tại A có: \(AB^2+AC^2=BC^2\Leftrightarrow6^2+8^2=BC^2\Rightarrow BC=10cm\)
Xét tam giác ABC vuông tại A có AM là đường trung tuyến ứng với cạnh huyền
\(\Rightarrow AM=\dfrac{BC}{2}=\dfrac{10}{2}=5cm\)
b. Xét tứ giác AKMN có: \(\left\{{}\begin{matrix}\widehat{A}=90^o\\\widehat{M}=90^o\\\widehat{N}=90^o\end{matrix}\right.\)
\(\Rightarrow\) Tứ giác AKMN là hình chữ nhật
c. Ta có: AM=MC \(\Rightarrow\Delta MCA\) cân tại M
\(\Rightarrow\)MN vừa là đường cao vừa là đường trung tuyến
\(\Rightarrow AN=NC\)
Tương tự với tam giác AMB \(\Rightarrow AK=KB\)
Xét tam giác ABC có: \(\left\{{}\begin{matrix}AN=NC\\AK=KB\end{matrix}\right.\)
\(\Rightarrow KN\) là đường trung bình của tam giác ABC
\(\Rightarrow KN//BC\)\(\Rightarrow KN//MC\)
Lại có: \(\left\{{}\begin{matrix}CA\perp AB\\KM\perp AB\end{matrix}\right.\)\(\Rightarrow CA//KM\)
Xét tứ giác KMCN có: \(\left\{{}\begin{matrix}KN//MC\\CN//KN\end{matrix}\right.\)
\(\Rightarrow\) Tứ giác KMCN là hình bình hành
d. Xét tam giác ABC có: \(\left\{{}\begin{matrix}AN=NC\\CM=MB\end{matrix}\right.\)
\(\Rightarrow NM\) là đường trung bình của tam giác ABC
\(\Rightarrow MN=\dfrac{AB}{2}\)
Xét tam giác AHB vuông tại H có HK là đường trung tuyến ứng với cạnh huyền
\(\Rightarrow HK=\dfrac{AB}{2}\)
\(\Rightarrow MN=HK\)
Xét tứ giác KHMN có: \(\left\{{}\begin{matrix}NK//MH\\NM=KH\end{matrix}\right.\)
\(\Rightarrow\) Tứ giác KHMN là hình thang cân

Bài 5:
\(x^2+y^2+1\ge xy+x+y\)
\(\Leftrightarrow2\left(x^2+y^2+1\right)\ge2\left(xy+x+y\right)\)
\(\Leftrightarrow2x^2+2y^2+2\ge2xy+2x+2y\)
\(\Leftrightarrow2x^2+2y^2+2-2xy-2x-2y\ge0\)
\(\Leftrightarrow\left(x^2-2xy+y^2\right)+\left(x^2-2x+1\right)+\left(y^2-2y+1\right)\ge0\)
\(\Leftrightarrow\left(x-y\right)^2+\left(x-1\right)^2+\left(y-1\right)^2\ge0\left(đúng\right)\)
-Dấu bằng xảy ra \(\Leftrightarrow x=y=1\)

a: Xét ΔMEB vuông tại M và ΔACB vuông tại A có
\(\widehat{B}\) chung
Do đó: ΔMEB\(\sim\)ΔACB
Xét ΔDMC vuông tại M và ΔABC vuông tại A có
\(\widehat{C}\) chung
Do đó: ΔDMC\(\sim\)ΔABC
b: BC=30cm

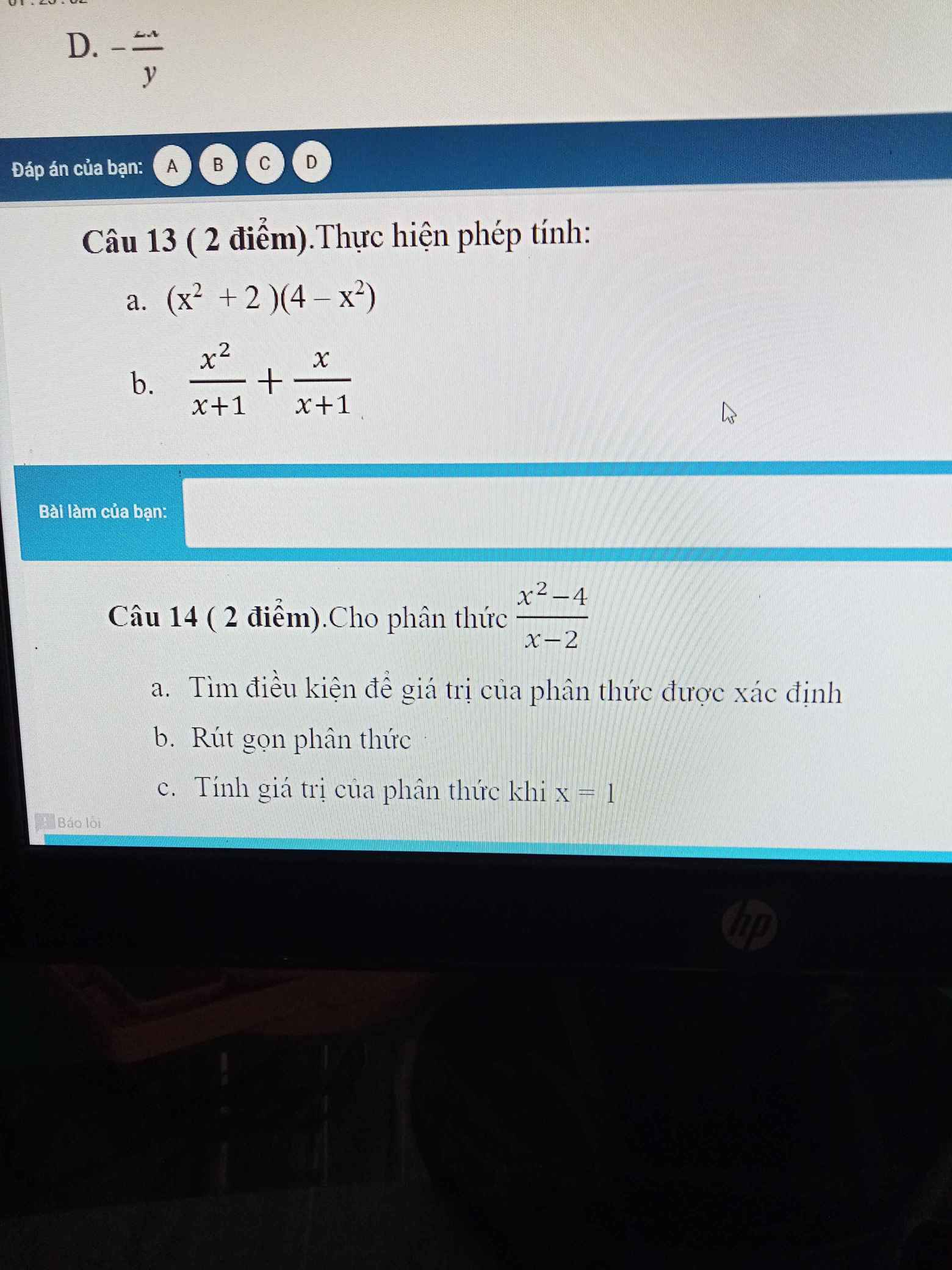
Câu 14;
a: ĐKXĐ: x<>2
b: \(\dfrac{x^2-4}{x-2}=x+2\)
c: Thay x=1 vào x+2, ta được:
x+2=1+2=3
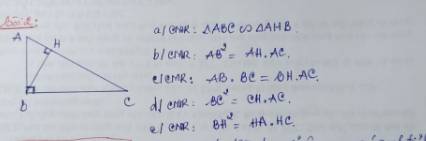






a) Xét hai tam giác vuông: \(\Delta ABC\) và \(\Delta AHB\) có:
\(\widehat{A}\) chung
\(\Rightarrow\Delta ABC\sim\Delta AHB\) (g-g)
b) Do \(\Delta ABC\sim\Delta AHB\) (cmt)
\(\Rightarrow\dfrac{AB}{AH}=\dfrac{AC}{AB}\)
\(\Rightarrow AB^2=AH.AC\)
c) Xét hai tam giác vuông: \(\Delta ABC\) và \(\Delta BHC\) có:
\(\widehat{C}\) chung
\(\Rightarrow\Delta ABC\sim\Delta BHC\) (g-g)
\(\Rightarrow\dfrac{AB}{BH}=\dfrac{AC}{BC}\)
\(\Rightarrow AB.BC=BH.AC\)
d) Do \(\Delta ABC\sim\Delta AHB\) (cmt)
\(\Delta ABC\sim\Delta BHC\) (cmt)
\(\Rightarrow\Delta AHB\sim\Delta BHC\)
\(\Rightarrow\dfrac{AH}{BH}=\dfrac{BH}{HC}\)
\(\Rightarrow BH^2=AH.HC\)
a: Xét ΔHAB vuông tại H và ΔBAC vuông tại B có
góc A chung
=>ΔHAB đồng dạng với ΔBAC
b: ΔHAB đồng dạng với ΔBAC
=>HA/BA=AB/AC=HB/BC
=>AB^2=AH*AC
c: HB/BC=AB/AC
=>HB*AC=BA*BC
d,e: ΔACB vuông tại B có BH là đường cao
nên BC^2=CH*CA và BH^2=HA*HC