Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Ta có: x(3 + 5i) - y(1 + 2i) = 9 + 16i <=> (3x - y) + (5x - 2y) = 9 + 16i
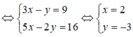
Vậy: T = |x - y| = 5

Ta có: (x + 2y) + (2x - y)i = 6 + 7i
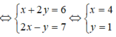
Vậy: T = 4 + 1 = 5
Chọn B

d)
TXĐ: $\mathbb{R}$
Ta có: $y=\sqrt{(x^2-3x-2)^2}$ nên $y'=\frac{(2x-3)(x^2-3x-2)}{|x^2-3x-2|}$
Hàm số không có đạo hàm tại $x^2-3x-2=0\Leftrightarrow x=\frac{3\pm \sqrt{17}}{2}$
\(y'=0\Leftrightarrow \left\{\begin{matrix} (2x-3)(x^2-3x-2)=0\\ x\in\mathbb{R}\setminus \left\{\frac{3\pm \sqrt{17}}{2}\right\}\end{matrix}\right.\Leftrightarrow x=\frac{3}{2}\)
BBT:

Vậy hàm số đồng biến trên mỗi khoảng $(\frac{3-\sqrt{17}}{2}; \frac{3}{2})$ và $(\frac{3+\sqrt{17}}{2}; +\infty)$, nghịch biến trên mỗi khoảng $(-\infty; \frac{3-\sqrt{17}}{2})$ và $(\frac{3}{2}; \frac{3+\sqrt{17}}{2})$
c)
TXĐ: $[2;4]$
Ta có:
\(y'=\frac{1}{2}\left(\frac{1}{\sqrt{x-2}}-\frac{1}{\sqrt{4-x}}\right)\). Hàm số không có đạo hàm tại $x=2; x=4$
\(y'=0\Leftrightarrow \left\{\begin{matrix} \sqrt{x-2}=\sqrt{4-x}\\ x\in (2;4)\end{matrix}\right.\Leftrightarrow x=3\)
BBT:

Vậy $y$ đồng biến trên khoảng $(2;3)$ và nghịch biến trên khoảng $(3;4)$