K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
20 tháng 8 2021
Bài 1:
b: Ta có: \(\left(\dfrac{\sqrt{14}-\sqrt{7}}{1-\sqrt{2}}-\dfrac{\sqrt{15}-\sqrt{5}}{1-\sqrt{3}}\right):\dfrac{1}{\sqrt{7}+\sqrt{5}}\)
\(=\left(-\sqrt{7}+\sqrt{5}\right)\cdot\left(\sqrt{7}+\sqrt{5}\right)\)
=5-7
=-2
20 tháng 8 2021
b) \(\left(\dfrac{\sqrt{14}-\sqrt{7}}{1-\sqrt{2}}-\dfrac{\sqrt{15}-\sqrt{5}}{1-\sqrt{3}}\right):\dfrac{1}{\sqrt{7}+\sqrt{5}}\)
\(=\left(\dfrac{\sqrt{7}\left(\sqrt{2}-1\right)}{-\left(\sqrt{2}-1\right)}-\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{-\left(\sqrt{3}-1\right)}\right):\dfrac{1}{\sqrt{7}+\sqrt{5}}\)
\(=\left(\sqrt{5}-\sqrt{7}\right).\left(\sqrt{5}+\sqrt{7}\right)\)
\(=5-7\\ =-2\)
MM
1
MM
1
20 tháng 12 2021
Câu 1:
\(a,=4\sqrt{3}-10\sqrt{3}+8\sqrt{3}=2\sqrt{3}\\ b,=3-\sqrt{5}+\sqrt{5}-1=2\)
Câu 2:
\(a,ĐK:x\ge-2\\ PT\Leftrightarrow4\sqrt{x+2}-3\sqrt{x+2}+\sqrt{x+2}=6\\ \Leftrightarrow\sqrt{x+2}=3\Leftrightarrow x+2=9\Leftrightarrow x=7\left(tm\right)\\ b,\Leftrightarrow\left\{{}\begin{matrix}x+2y=1\\5y=15\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-5\\y=3\end{matrix}\right.\)
Câu 3:
\(b,PTHDGD:2x-3=-x+3\Leftrightarrow x=2\Leftrightarrow y=1\Leftrightarrow A\left(2;1\right)\\ c,\Leftrightarrow A\left(2;1\right)\in\left(d_3\right)\Leftrightarrow2m-6+m=1\Leftrightarrow m=\dfrac{7}{3}\)
1 tháng 9 2021
a: Ta có: \(2\sqrt{28}+3\sqrt{63}-3\sqrt{\dfrac{112}{9}}-\sqrt{\dfrac{196}{7}}\)
\(=4\sqrt{7}+9\sqrt{7}-4\sqrt{7}-2\sqrt{7}\)
\(=7\sqrt{7}\)
b: Ta có: \(\sqrt{8+2\sqrt{7}}-\sqrt{12-\sqrt{140}}-\sqrt{5}\)
\(=\sqrt{7}+1-\sqrt{7}+\sqrt{5}-\sqrt{5}\)
=1
TT
3
15 tháng 9 2021
a) \(A=\dfrac{x+\sqrt{xy}}{y+\sqrt{xy}}=\dfrac{\sqrt{x}\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{y}\left(\sqrt{x}+\sqrt{y}\right)}=\dfrac{\sqrt{x}}{\sqrt{y}}\)
b) \(B=\dfrac{\sqrt{a}+a\sqrt{b}-\sqrt{b}-b\sqrt{a}}{ab-1}=\dfrac{\sqrt{a}\left(1+\sqrt{ab}\right)-\sqrt{b}\left(1+\sqrt{ab}\right)}{\left(\sqrt{ab}-1\right)\left(1+\sqrt{ab}\right)}=\dfrac{\left(1+\sqrt{ab}\right)\left(\sqrt{a}-\sqrt{b}\right)}{\sqrt{ab}-1}=\dfrac{\sqrt{a}-\sqrt{b}}{\sqrt{ab}-1}\)
15 tháng 9 2021
c) \(C=\dfrac{1+x\sqrt{x}}{1+\sqrt{x}}=\dfrac{\left(1+\sqrt{x}\right)\left(1-\sqrt{x}+x\right)}{1+\sqrt{x}}=1-\sqrt{x}+x\)
d) \(D=\dfrac{x\sqrt{x}+y\sqrt{y}}{\sqrt{x}+\sqrt{y}}-\left(\sqrt{x}-\sqrt{y}\right)^2=\dfrac{\left(\sqrt{x}+\sqrt{y}\right)\left(x-\sqrt{xy}+y\right)}{\sqrt{x}+\sqrt{y}}-x+2\sqrt{xy}-y=x-\sqrt{xy}+y-x+2\sqrt{xy}-y=\sqrt{xy}\)
e) \(\dfrac{x+4\sqrt{x}+4}{\sqrt{x}+2}+\dfrac{4-x}{2-\sqrt{x}}=\dfrac{\left(\sqrt{x}+2\right)^2}{\sqrt{x}+2}+\dfrac{\left(2-\sqrt{x}\right)\left(2+\sqrt{x}\right)}{2-\sqrt{x}}=\sqrt{x}+2+2+\sqrt{x}=2\sqrt{x}+4\)
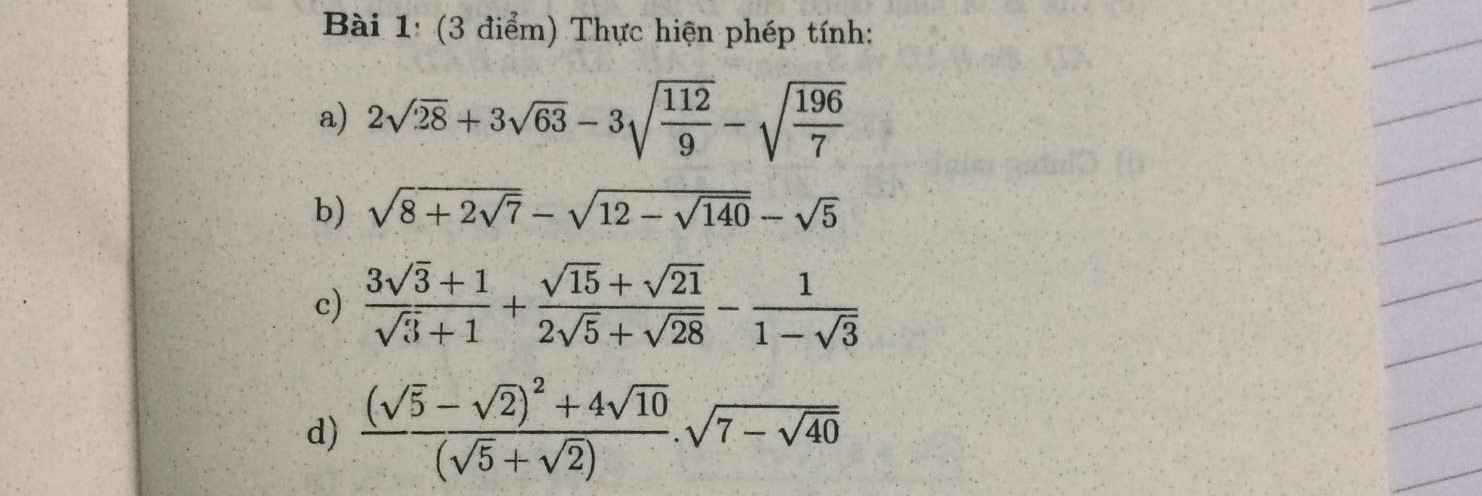
Bài 2:
a: Xét ΔABC vuông tại A có
\(AB=BC\cdot\sin50^0\)
\(\Leftrightarrow AB\simeq30,64\left(cm\right)\)
\(\Leftrightarrow AC=\sqrt{40^2-30.64^2}\simeq25,71\left(cm\right)\)