K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 3 2022
\(y=\left(x^7+x\right)^3\)
\(y'=3\left(x^7+x\right)^2.\left(x^7+x\right)'=3\left(x^7+x\right)^2\left(7x^6+1\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 4 2022
7.
\(y'=3x^2+8x-1\)
\(\Rightarrow y'\left(2\right)=3.2^2+8.2-1=27\)
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 4 2022
7.
\(y'=\left(-x^3\right)'-\left(5x\right)'+\left(2\right)'=-3x^2-5\)
\(y''=\left(-3x^2\right)'-\left(5\right)'=-6x\)
8.
\(\lim\limits_{x\rightarrow+\infty}\left(x^3+3x-2\right)=\lim\limits_{x\rightarrow+\infty}x^3\left(1+\dfrac{3}{x^2}-\dfrac{2}{x^3}\right)\)
Do: \(\lim\limits_{x\rightarrow+\infty}x^3=+\infty\)
\(\lim\limits_{x\rightarrow+\infty}\left(1+\dfrac{3}{x^2}-\dfrac{2}{x^3}\right)=1>0\)
\(\Rightarrow\lim\limits_{x\rightarrow+\infty}x^3\left(1+\dfrac{3}{x^2}-\dfrac{2}{x^3}\right)=+\infty\)
TB
26 tháng 10 2021
\(4\sin^22x-4\cos2x-1=0\)
\(\Leftrightarrow4\left(1-\cos^22x\right)-4\cos2x-1=0\)
\(\Leftrightarrow4-4\cos^22x-4\cos2x-1=0\)
\(\Leftrightarrow-4\cos^22x-4\cos2x+3=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=\dfrac{1}{2}\\cos2x=\dfrac{-3}{2}\left(L\right)\end{matrix}\right.\Leftrightarrow\cos2x=\dfrac{1}{2}\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{3}+k2\pi\\2x=-\dfrac{\pi}{3}-k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=-\dfrac{\pi}{6}-k\pi\end{matrix}\right.\left(k\in Z\right)\)
Chọn A
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 12 2021
Mỗi câu hỏi có \(\dfrac{1}{4}\) khả năng trả lời đúng và \(\dfrac{3}{4}\) khả năng trả lời sai
Có 3 trường hợp thỏa mãn: học sinh trả lời đúng 7 câu, 8 câu, 9 câu
Xác suất:
\(P=C_9^7.\left(\dfrac{1}{4}\right)^7.\left(\dfrac{3}{4}\right)^2+C_9^8.\left(\dfrac{1}{4}\right)^8.\left(\dfrac{3}{4}\right)^1+C_9^9.\left(\dfrac{1}{4}\right)^9=\dfrac{11}{8192}\)
27 tháng 7 2023
a: BA vuông góc AD
BA vuông góc SA
=>BA vuông góc (SAD)
b: CD vuông góc AD
CD vuông góc SA
=>CD vuông góc (SAD)
=>(SCD) vuông góc (SAD)
c: (SD;(ABCD))=(DS;DA)=góc SDA
tan SDA=SA/AD=căn 6/2
=>góc SDA=51 độ
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 3 2022
\(\lim\limits_{x\rightarrow1}f\left(x\right)=\lim\limits_{x\rightarrow1}\dfrac{mx^2-\left(m+3\right)x+3}{x-1}=\lim\limits_{x\rightarrow1}\dfrac{\left(x-1\right)\left(mx-3\right)}{x-1}\)
\(=\lim\limits_{x\rightarrow1}\left(mx-3\right)=m-3\)
\(f\left(1\right)=m^2-15\)
Hàm liên tục tại \(x=1\) khi:
\(m-3=m^2-15\Rightarrow m^2-m-12=0\Rightarrow\left[{}\begin{matrix}m=4\\m=-3\end{matrix}\right.\)
\(4^2+\left(-3\right)^2=25\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 4 2022
\(y'=3x^2-2\)
hệ số góc tiếp tuyến tại điểm có hoành độ \(x_0=-1\) là \(y'\left(-1\right)\)
\(y'\left(-1\right)=3.\left(-1\right)^2-2=1\)
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 4 2022
19. Giới hạn đã cho hữu hạn khi và chỉ khi \(a=1\)
Khi đó:
\(\lim\limits_{x\rightarrow+\infty}\left(x-\sqrt{x^2+bx-2}\right)=\lim\limits_{x\rightarrow+\infty}\dfrac{x^2-\left(x^2+bx-2\right)}{x+\sqrt{x^2+bx-2}}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{-bx+2}{x+\sqrt{x^2+bx-2}}=\lim\limits_{x\rightarrow+\infty}\dfrac{-b+\dfrac{2}{x}}{1+\sqrt{1+\dfrac{b}{x}-\dfrac{2}{x^2}}}=-\dfrac{b}{2}\)
\(\Rightarrow-\dfrac{b}{2}=3\Rightarrow b=-6\Rightarrow a+b=1+\left(-6\right)=-5\)
20.
\(\lim\limits_{x\rightarrow+\infty}\left(x^3+2x-1\right)=\lim\limits_{x\rightarrow+\infty}x^3\left(1+\dfrac{2}{x^2}-\dfrac{1}{x^3}\right)=+\infty.1=+\infty\)
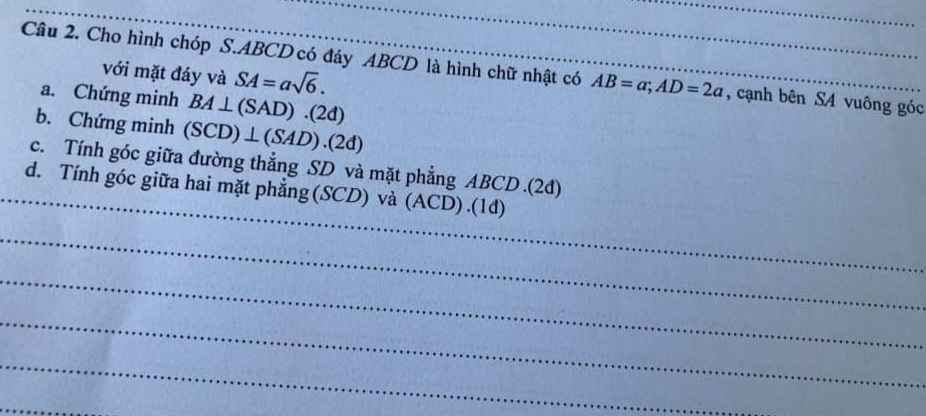
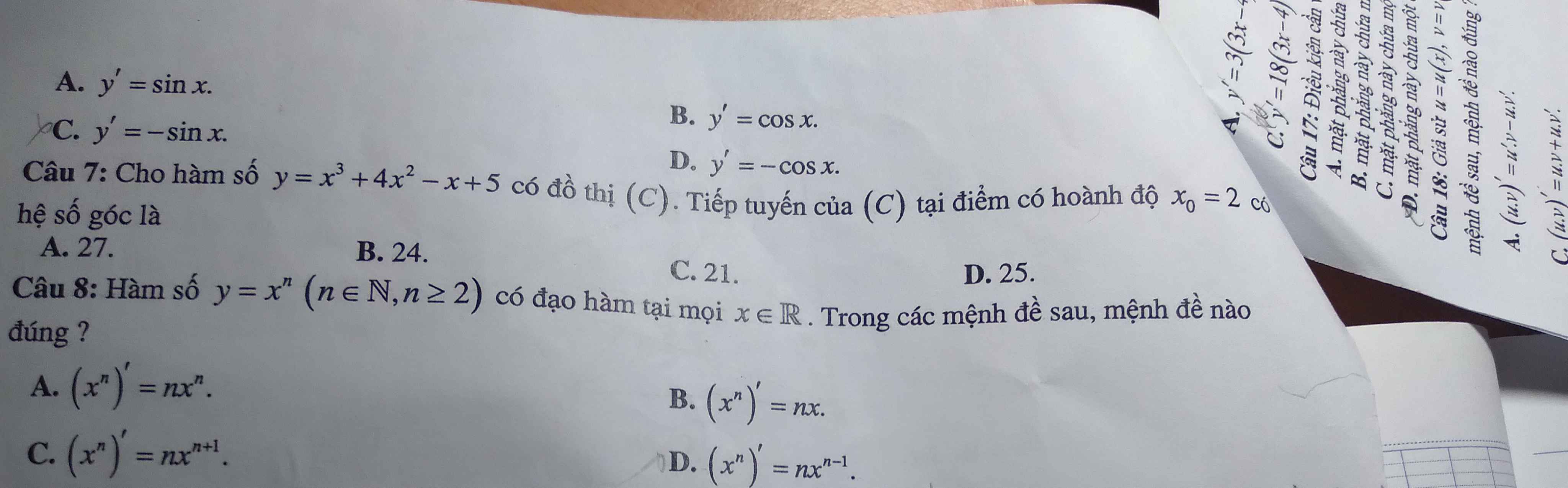
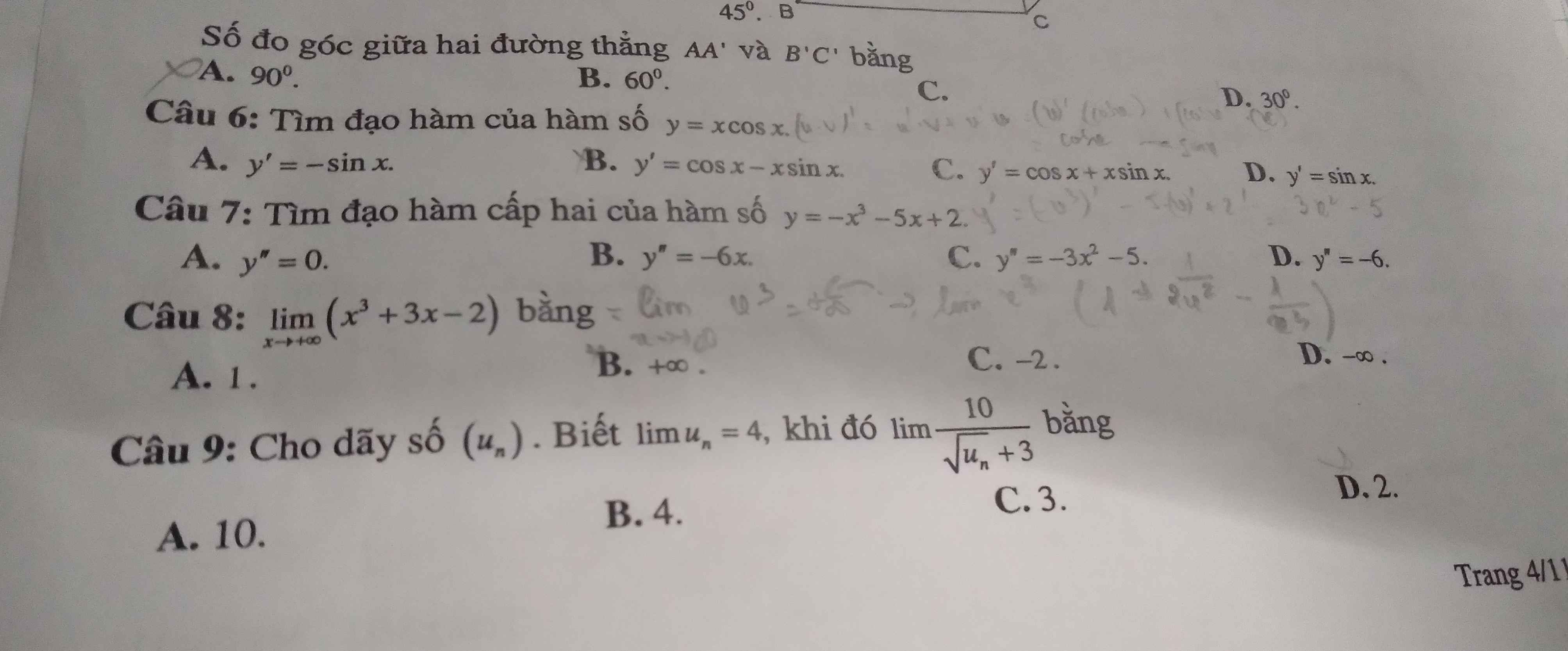
a.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp AB\\AB\perp AD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow AB\perp\left(SAD\right)\)
b.
Ta có \(CD||AB\) (do ABCD là hcn)
Mà \(AB\perp\left(SAD\right)\Rightarrow CD\perp\left(SAD\right)\)
Lại có \(CD\in\left(SCD\right)\)
\(\Rightarrow\left(SCD\right)\perp\left(SAD\right)\)
c.
\(SA\perp\left(ABCD\right)\Rightarrow AD\) là hình chiếu vuông góc của SD lên (ABCD)
\(\Rightarrow\widehat{SDA}\) là góc giữa SD và (ABCD)
\(tan\widehat{SDA}=\dfrac{SA}{AD}=\dfrac{\sqrt{6}}{2}\Rightarrow\widehat{SDA}\approx50^046'\)
d.
Ta có: \(SA\perp\left(ABCD\right)\Rightarrow SA\perp\left(ACD\right)\)
Mà \(SA\in\left(SAD\right)\Rightarrow\left(SAD\right)\perp\left(ACD\right)\) (1)
Theo câu b ta có: \(\left(SAD\right)\perp\left(SCD\right)\) (2)
(1);(2) \(\Rightarrow\widehat{SDA}\) là góc giữa (SCD) và (ACD)
Theo câu c ta có: \(\widehat{SDA}=50^046'\)