
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(x^2-4x+m=0\)
Để pt có 2 nghiệm \(x_1,x_2\Leftrightarrow\Delta\ge0\Leftrightarrow\left(-4\right)^2-4m\ge0\Leftrightarrow m\le4\)
Theo Vi-ét, ta có :
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=4\\x_1x_2=\dfrac{c}{a}=m\end{matrix}\right.\)
Ta có :
\(2x_1+x_2=7\)
\(\Leftrightarrow\left\{{}\begin{matrix}2=\dfrac{x_1+x_2}{2}\\2x_1+x_2=7\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2=4\\2x_1+x_2=7\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1=3\\x_2=1\end{matrix}\right.\)
Thay \(x_1x_2=m\Leftrightarrow m=3.1=3\left(tmdk\right)\)
Vậy m = 3 thì pt có 2 nghiệm \(x_1,x_2\) thỏa mãn \(2x_1+x_2=7\)

ĐKXĐ: \(x^2+5x+2>=0\)
=>\(\left[{}\begin{matrix}x>=\dfrac{-5+\sqrt{17}}{2}\\x< =\dfrac{-5-\sqrt{17}}{2}\end{matrix}\right.\)
\(\left(x+1\right)\left(x+4\right)-3\sqrt{x^2+5x+2}=6\)
=>\(x^2+5x+4-3\sqrt{x^2+5x+2}-6=0\)
=>\(x^2+5x+2-3\sqrt{x^2+5x+2}-4=0\)(1)
Đặt \(\sqrt{x^2+5x+2}=a\)(a>=0)
Phương trình (1) trở thành:
\(a^2-3a-4=0\)
=>(a-4)(a+1)=0
=>\(\left[{}\begin{matrix}a=4\left(nhận\right)\\a=-1\left(loại\right)\end{matrix}\right.\)
=>\(x^2+5x+2=4^2=16\)
=>\(x^2+5x-14=0\)
=>\(\left(x+7\right)\left(x-2\right)=0\)
=>\(\left[{}\begin{matrix}x=-7\left(nhận\right)\\x=2\left(nhận\right)\end{matrix}\right.\)

\(b,B=\dfrac{\sqrt{x}+2}{\sqrt{x}-3}+\dfrac{\sqrt{x}-8}{x-5\sqrt{x}+6}\left(x\ge0;x\ne4;x\ne9\right)\\ B=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)+\sqrt{x}-8}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\\ B=\dfrac{x-4+\sqrt{x}-8}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-4\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}-4}{\sqrt{x}-2}\)
\(c,B< A\Leftrightarrow\dfrac{\sqrt{x}-4}{\sqrt{x}-2}< \dfrac{\sqrt{x}+1}{\sqrt{x}-2}\Leftrightarrow\dfrac{\sqrt{x}-4}{\sqrt{x}-2}-\dfrac{\sqrt{x}+1}{\sqrt{x}-2}< 0\\ \Leftrightarrow\dfrac{-5}{\sqrt{x}-2}< 0\Leftrightarrow\sqrt{x}-2>0\left(-5< 0\right)\\ \Leftrightarrow x>4\\ d,P=\dfrac{B}{A}=\dfrac{\sqrt{x}-4}{\sqrt{x}-2}:\dfrac{\sqrt{x}+1}{\sqrt{x}-2}=\dfrac{\sqrt{x}-4}{\sqrt{x}+1}=1-\dfrac{5}{\sqrt{x}+1}\in Z\\ \Leftrightarrow5⋮\sqrt{x}+1\Leftrightarrow\sqrt{x}+1\inƯ\left(5\right)=\left\{-5;-1;1;5\right\}\\ \Leftrightarrow\sqrt{x}\in\left\{-6;-2;0;4\right\}\\ \Leftrightarrow x\in\left\{0;16\right\}\left(\sqrt{x}\ge0\right)\)
\(e,P=1-\dfrac{5}{\sqrt{x}+1}\)
Ta có \(\sqrt{x}+1\ge1,\forall x\Leftrightarrow\dfrac{5}{\sqrt{x}+1}\ge5\Leftrightarrow1-\dfrac{5}{\sqrt{x}+1}\le-4\)
\(P_{max}=-4\Leftrightarrow x=0\)

PT <=> \(x^2-4x\left(y-1\right)+5y^2-8y-12=0\)
Xét \(\Delta'=\left[-2\left(y-1\right)\right]^2-1.\left(5y^2-8y-12\right)\)
= \(4\left(y^2-2y+1\right)-5y^2+8y+12\)
= \(-y^2+16\)
Để PT có nghiệm <=> \(\Delta'\ge0< =>-y^2+16\ge0\)
<=> \(y^2\le16\) <=> \(-4\le y\le4\)
Mà y nguyên
<=> \(y\in\left\{-4;-3;-2;-1;0;1;2;3;4\right\}\)
Đến đây bn thay y vào PT để tìm x nhé

Điểm trên trục tung có tung độ -2 có tọa độ là \(\left(0;-2\right)\)
Đường thẳng song song với \(y=2x-1\Rightarrow a=2\)
\(\Rightarrow y=2x+b\)
Đường thẳng đi qua điểm (0;-2) nên:
\(-2=2.0+b\Rightarrow b=-2\)
Vậy pt đường thẳng có dạng: \(y=2x-2\)

Bài 1:
3: ĐKXĐ: x>=1
\(x-\sqrt{x+3+4\sqrt{x-1}}=1\)
=>\(x-\sqrt{x-1+2\cdot\sqrt{x-1}\cdot2+4}=1\)
=>\(x-\sqrt{\left(\sqrt{x-1}+2\right)^2}=1\)
=>\(x-\left|\sqrt{x-1}+2\right|=1\)
=>\(x-\left(\sqrt{x-1}+2\right)=1\)
=>\(x-\sqrt{x-1}-2-1=0\)
=>\(x-1-\sqrt{x-1}-2=0\)
=>\(\left(\sqrt{x-1}\right)^2-2\sqrt{x-1}+\sqrt{x-1}-2=0\)
=>\(\left(\sqrt{x-1}-2\right)\left(\sqrt{x-1}+1\right)=0\)
=>\(\sqrt{x-1}-2=0\)
=>\(\sqrt{x-1}=2\)
=>x-1=4
=>x=5(nhận)


\(\hept{\begin{cases}3x-2y=xy\\4x+y=5xy\end{cases}\Leftrightarrow\hept{\begin{cases}3x-2y=xy\\8x+2y=10xy\end{cases}\Leftrightarrow}\hept{\begin{cases}11x=11xy\\3x-2y=xy\end{cases}}}\)
\(\Leftrightarrow\hept{\begin{cases}x=xy\\3x-2y=xy\end{cases}\Leftrightarrow\hept{\begin{cases}y=1\\3x-2=x\end{cases}\Leftrightarrow}\hept{\begin{cases}y=1\\2x=2\end{cases}}}\Leftrightarrow\hept{\begin{cases}y=1\\x=1\end{cases}}\)
vậy hệ PT có nghiệm duy nhất là (x;y) =( 1;1)
Thiếu nghiệm rồi bạn @Lyzimi ơi. Còn nghiệm \(\left(0;0\right)\) nữa.

\(\hept{\begin{cases}x^2+y^2+4xy=6\left(1\right)\\4x^2+16=6y+14x\left(2\right)\end{cases}}\)
Lấy (1) + (2) vế theo vế rồi chuyển tất cả sang vế trái ta được
5x2 + y2 + 4xy + 10 - 6y -14x = 0
<=> (4x2 + 4xy + y2) - 6(2x + y) + 9 + (x2 - 2x + 1) = 0
<=> (2x + y)2 - 6(2x + y) + 9 + (x - 1)2 = 0
<=> ( 2x + y - 3)2 + (x - 1)2 = 0
\(\Leftrightarrow\hept{\begin{cases}2x+y-3=0\\x-1=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=1\\y=1\end{cases}}\)
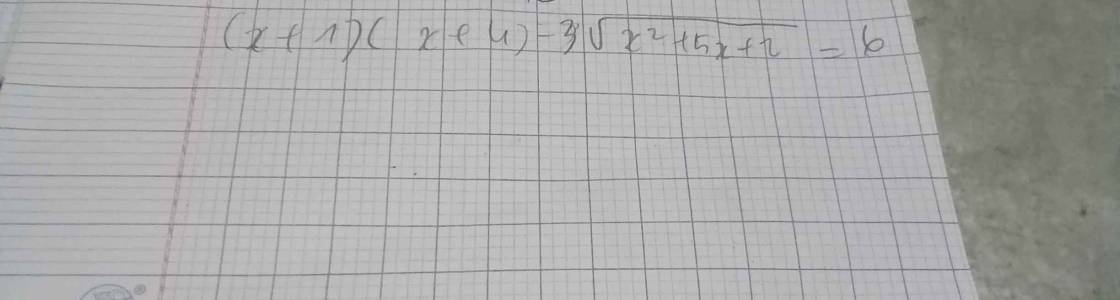



Em ơi ch đủ đề