K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
28 tháng 9 2021
chu vi hình vuông là
50x4=200cm
độ dài 1 cạnh hình vuông là
50:4=12,5cm
diện tích hình vuông là
12,5x12,5=156,25cm2
18 tháng 6 2023
a: DB/DC=AB/AC=4/3
b: BC=căn 6^2+8^2=10cm
DB/4=DC/3=10/7
=>DB=40/7cm; DC=30/7cm
c: Xét ΔAHB vuông tại H và ΔCHA vuông tại H có
góc HAB=góc HCA
=>ΔHAB đồng dạng với ΔHCA
LC
1
21 tháng 11 2023
a: Xét ΔHAC vuông tại H và ΔABC vuông tại A có
\(\widehat{C}\) chung
Do đó: ΔHAC~ΔABC
b: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=15^2+20^2=625\)
=>BC=25
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}BH\cdot BC=BA^2\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH\cdot25=15^2=225\\AH\cdot25=15\cdot20=300\end{matrix}\right.\)
=>BH=9; AH=12
26 tháng 10 2021
Bài 1:
a: \(36a^4-y^2=\left(6a^2-y\right)\left(6a^2+y\right)\)
n: \(6x^2+x-2\)
\(=6x^2+4x-3x-2\)
\(=\left(3x+2\right)\left(2x-1\right)\)
HT
4
LP
19 tháng 8 2021
3x.(x-2)-x2+2x=0
⇔3x2-6x-x2+2x=0
⇔2x2-4x=0
⇔2x(x-2)=0
\(\Leftrightarrow\left[{}\begin{matrix}2x=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
vậy x=0 và x=2
19 tháng 8 2021
3x(x-2)-x^2+2x=0
<=>3x(x-2)-x(x-2)=0
<=>(3x-x)(x-2)=0
<=>2x(x-2)=0
<=>2x=0 hoặc x-2=0
<=>x=0 hoặc x=2
13 tháng 3 2022
\(PT\left(x\ne\dfrac{7}{2};\dfrac{-7}{2}\right).\\\Leftrightarrow \dfrac{8x+28-35+10x-4-3x}{\left(7-2x\right)\left(7+2x\right)}=0.\\ \Rightarrow15x=11.\)
\(\Leftrightarrow x=\dfrac{11}{15}\left(TM\right).\)
TM
13 tháng 3 2022
\(\dfrac{4}{7-2x}=\dfrac{5}{2x+7}-\dfrac{4+3x}{4x^2-49}\left(a\right)\)
Ta có : \(4x^2-49=\left(2x+7\right)\left(2x-7\right)\)
\(\RightarrowĐKXĐ:\left\{{}\begin{matrix}7-2x\ne0\\2x+7\ne0\\2x-7\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{7}{2}\\x\ne-\dfrac{7}{2}\\x\ne\dfrac{7}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{7}{2}\\x\ne-\dfrac{7}{2}\end{matrix}\right.\)
\(\left(a\right)\Leftrightarrow\dfrac{-4}{2x-7}=\dfrac{5}{2x+7}-\dfrac{4+3x}{4x^2-49}\)
\(\Leftrightarrow\dfrac{-4\left(2x+7\right)}{\left(2x-7\right)\left(2x+7\right)}=\dfrac{5\left(2x-7\right)}{\left(2x-7\right)\left(2x+7\right)}-\dfrac{4+3x}{\left(2x-7\right)\left(2x+7\right)}\left(a_1\right)\)
- Khử mẫu ta được :
\(\left(a_1\right)\Leftrightarrow-4\left(2x+7\right)=5\left(2x-7\right)-\left(4+3x\right)\)
\(\Leftrightarrow-8x-28=10x-35-4-3x\)
\(\Leftrightarrow-8x-10x+3x=28-35-4\)
\(\Leftrightarrow-15x=-11\)
\(\Leftrightarrow x=\dfrac{11}{15}\left(tmđk\right)\)
Vậy : Phương trình có tập nghiệm \(S=\left\{\dfrac{11}{15}\right\}\)
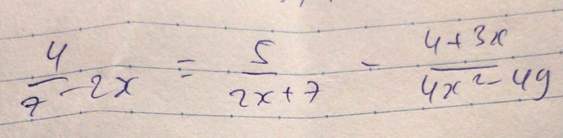
a: Xét ΔADE vuông tại E và ΔCBF vuông tại F có
AD=BC
\(\widehat{ADE}=\widehat{CBF}\)
Do đó: ΔADE=ΔCBF
Suy ra: AE=CF
Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
b: Xét tứ giác AICK có
AI//CK
AK//IC
Do đó: AICK là hình bình hành
Suy ra: AI=CK
c: Ta có: ΔADE=ΔCBF
nên DE=BF