Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Trong mp(ABCD), Gọi giao của AC và BD là O
\(O\in AC\subset\left(SAC\right)\)
\(O\in BD\subset\left(SBD\right)\)
Do đó: \(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà S thuộc (SAC) giao (SBD)
nên (SAC) giao (SBD)=SO
b:Trong mp(ABCD), Gọi giao của AB và CD là M
\(M\in AB\subset\left(SAB\right)\)
\(M\in CD\subset\left(SCD\right)\)
=>M thuộc (SAB) giao (SCD)
mà S thuộc (SAB) giao (SCD)
nên (SAB) giao (SCD)=SM
c: Trong mp(ABCD), gọi N là giao của AD với BC
\(N\in AD\subset\left(SAD\right);N\in BC\subset\left(SBC\right)\)
Do đó: \(N\in\left(SAD\right)\cap\left(SBC\right)\)
mà \(S\in\left(SAD\right)\cap\left(SBC\right)\)
nên \(\left(SAD\right)\cap\left(SBC\right)=SN\)

a: \(SB\subset\left(SAB\right)\)
\(SB\subset\left(SBD\right)\)
Do đó: \(\left(SAB\right)\cap\left(SBD\right)=SB\)
b: \(F\in SB\subset\left(SAB\right);F\in\left(SDF\right)\)
Do đó: \(F\in\left(SAB\right)\cap\left(SDF\right)\)
mà \(S\in\left(SAB\right)\cap\left(SDF\right)\)
nên \(\left(SAB\right)\cap\left(SDF\right)=SF\)
c: \(F\in SB\subset\left(SBC\right);F\in\left(FCD\right)\)
\(\Leftrightarrow F\in\left(SBC\right)\cap\left(FCD\right)\)
mà \(C\in\left(CBS\right)\cap\left(FCD\right)\)
nên \(\left(FCD\right)\cap\left(SBC\right)=CF\)

Để giải quyết các bài toán này, chúng ta cần sử dụng các kiến thức về hình học không gian và tính chất của các hình học trong không gian. Dưới đây là cách giải từng câu hỏi:
a) Để tìm giao điểm của SA (đường thẳng qua S và A) và mặt phẳng ABCD, chúng ta cần tìm điểm giao nhau của đường thẳng SA và mặt phẳng ABCD. Điểm giao nhau này sẽ nằm trên cạnh AD của hình chóp S.ABCD. Vì vậy, ta cần tìm điểm giao nhau của SA và AD.b) Để tìm giao điểm của BC và mặt phẳng SAD, chúng ta cần tìm điểm giao nhau của cạnh BC và mặt phẳng SAD. Điểm giao nhau này sẽ nằm trên cạnh AD của hình chóp S.ABCD. Vì vậy, ta cần tìm điểm giao nhau của BC và AD.
c) Để tìm giao điểm của AE và mặt phẳng SBD, chúng ta cần tìm điểm giao nhau của cạnh AE và mặt phẳng SBD. Điểm giao nhau này sẽ nằm trên cạnh BD của hình chóp S.ABCD. Vì vậy, ta cần tìm điểm giao nhau của AE và BD.
a) Để tìm giao điểm của SD và mặt phẳng ABCD, chúng ta cần tìm điểm giao nhau của cạnh SD và mặt phẳng ABCD. Điểm giao nhau này sẽ nằm trên cạnh AD của hình chóp S.ABCD. Vì vậy, ta cần tìm điểm giao nhau của SD và AD.b) Để tìm giao điểm của CD và mặt phẳng SAB, chúng ta cần tìm điểm giao nhau của cạnh CD và mặt phẳng SAB. Điểm giao nhau này sẽ nằm trên cạnh AB của hình chóp S.ABCD. Vì vậy, ta cần tìm điểm giao nhau của CD và AB.
c) Để tìm giao điểm của DF và mặt phẳng SAC, chúng ta cần tìm điểm giao nhau của cạnh DF và mặt phẳng SAC. Điểm giao nhau này sẽ nằm trên cạnh AC của hình chóp S.ABCD. Vì vậy, ta cần tìm điểm giao nhau của DF và AC.
Vì các bài toán này đòi hỏi tính toán chi tiết và cần biết thêm thông tin về các giá trị cụ thể của các đường thẳng và mặt phẳng, nên tôi không thể cung cấp câu trả lời chính xác mà chỉ có thể hướng dẫn cách giải quyết chúng.
1:
a: \(A\in SA\)
\(A\in\left(ABCD\right)\)
=>\(A=SA\cap\left(ABCD\right)\)
b: Gọi O là giao của AD và BC
\(O\in BC\)
\(O\in AD\subset\left(SAD\right)\)
=>\(O=BC\cap\left(SAD\right)\)
c: Chọn mp(SAC) có chứa AE
Gọi K là giao của BD và AC
\(K\in BD\subset\left(SBD\right);K\in AC\subset\left(SAC\right)\)
\(S\in SD\subset\left(SBD\right);S\in SA\subset\left(SAC\right)\)
Do đó: \(\left(SBD\right)\cap\left(SAC\right)=SK\)
Gọi F là giao của SK với AE
=>F là giao của AE với mp(SBD)

2:
a: \(D\in SD\)
\(D\in DB\subset\left(ABCD\right)\)
Do đó: \(SD\cap ABCD=D\)
b: Chọn mp(ABCD) có chứa CD
\(AB\subset\left(ABCD\right)\)
\(AB\subset\left(SAB\right)\)
Do đó: \(\left(SAB\right)\cap\left(ABCD\right)=AB\)
Gọi M là giao của AB và CD
=>\(M=CD\cap\left(SAB\right)\)
c: Chọn mp(SBD) có chứa DF
Gọi N là giao của BD và AC
\(N\in BD\subset\left(SBD\right)\)
\(N\in AC\subset\left(SAC\right)\)
Do đó: \(N\in\left(SBD\right)\cap\left(SAC\right)\)
=>\(\left(SBD\right)\cap\left(SAC\right)=SN\)
Gọi K là giao của SN với DF
=>\(K=DF\cap\left(SAC\right)\)

Gọi O là giao điểm AC và BD
\(\left\{{}\begin{matrix}O\in AC\in\left(SAC\right)\\O\in BD\in\left(SBD\right)\end{matrix}\right.\) \(\Rightarrow O=\left(SAC\right)\cap\left(SBD\right)\)
\(\left\{{}\begin{matrix}S\in\left(SAC\right)\\S\in\left(SBD\right)\end{matrix}\right.\) \(\Rightarrow S=\left(SAC\right)\cap\left(SBD\right)\)
\(\Rightarrow SO=\left(SAC\right)\cap\left(SBD\right)\)
b. Trong mp ((SAB), nối MN cắt AB tại E
\(\left\{{}\begin{matrix}E\in MN\in\left(CMN\right)\\E\in AB\in\left(ABCD\right)\end{matrix}\right.\) \(\Rightarrow E\in\left(CMN\right)\cap\left(ABCD\right)\)
\(\left\{{}\begin{matrix}C\in\left(CMN\right)\\C\in\left(ABCD\right)\end{matrix}\right.\) \(\Rightarrow C\in\left(CMN\right)\cap\left(ABCD\right)\)
\(\Rightarrow CE=\left(CMN\right)\cap\left(ABCD\right)\)

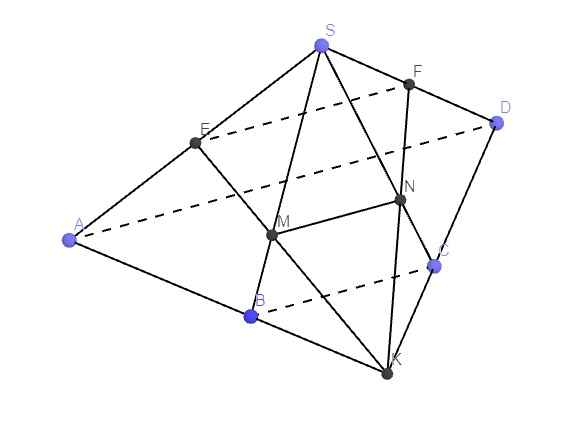
Áp dụng định lý Talet trong tam giác KAD:
\(\dfrac{KB}{KA}=\dfrac{KC}{KD}=\dfrac{BC}{AD}=\dfrac{1}{2}\)
\(\Rightarrow B,C\) lần lượt là trung điểm AK và DK
Mà E, F là trung điểm SA, SD
\(\Rightarrow\) M, N lần lượt là trọng tâm các tam giác SAK và SDK
\(\Rightarrow\dfrac{SM}{SB}=\dfrac{2}{3}\) ; \(\dfrac{SN}{SC}=\dfrac{2}{3}\)
\(\Rightarrow\dfrac{MN}{BC}=\dfrac{SM}{SB}=\dfrac{SN}{SC}=\dfrac{2}{3}\) (Talet)
\(\Rightarrow MN=\dfrac{2}{3}BC=\dfrac{2}{3}.\dfrac{1}{2}AD=\dfrac{1}{3}AD\)
Lại có EF là đường trung bình tam giác SAD \(\Rightarrow EF=\dfrac{1}{2}AD\)
\(\Rightarrow\dfrac{S_{KMN}}{S_{KEF}}=\dfrac{MN}{EF}=\dfrac{\dfrac{1}{3}AD}{\dfrac{1}{2}AD}=\dfrac{2}{3}\)

a: \(D\in SD\)
\(D\in\left(ABCD\right)\)
Do đó: \(SD\cap\left(ABCD\right)=D\)
b: Chọn mp(ABCD) có chứa CD
\(AB\subset\left(ABCD\right)\)
\(AB\subset\left(SAB\right)\)
Do đó: \(\left(SAB\right)\cap\left(ABCD\right)=AB\)
Gọi K là giao của AB và CD
=>\(K=CD\cap\left(SAB\right)\)


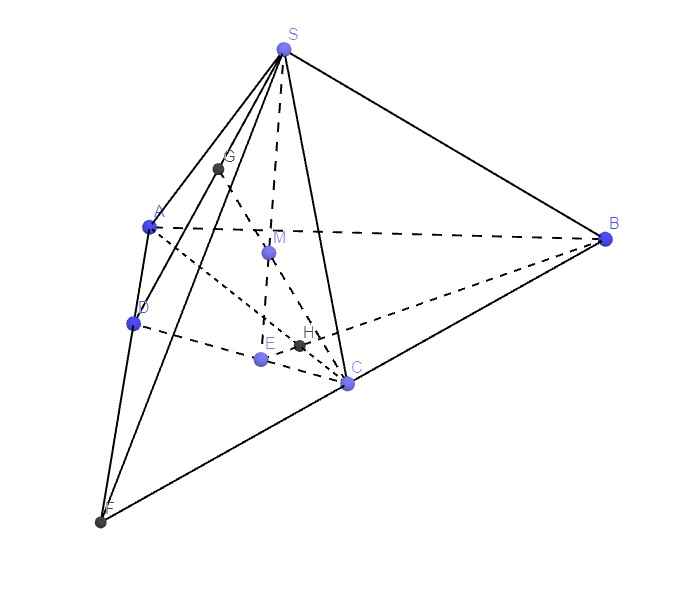
Nối BC và AD kéo dài cắt nhau tại F
\(\Rightarrow SF=\left(SBC\right)\cap\left(SAD\right)\)
Trong mp (SCD), nối CM kéo dài cắt SD tại G
\(\Rightarrow AG=\left(AMC\right)\cap\left(SAD\right)\)
Trong mp (SCD), nối SM kéo dài cắt CD tại E
\(\Rightarrow AE=\left(SAM\right)\cap\left(ABCD\right)\)
Trong mp (ABCD), nối BE cắt AC tại H
\(\Rightarrow SH=\left(SBM\right)\cap\left(SAC\right)\)

a.
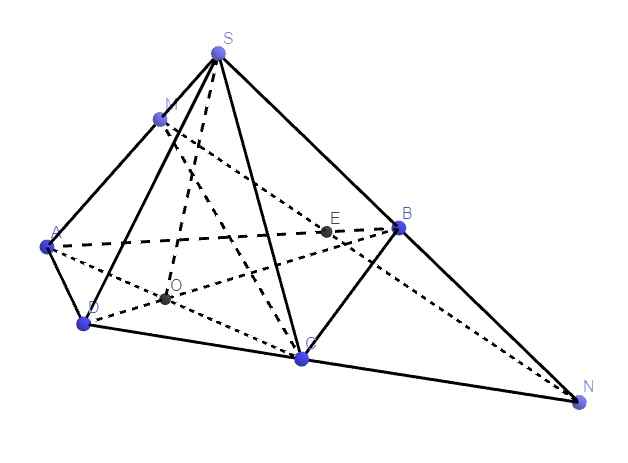
\(S\in\left(SAC\right)\cap\left(SBD\right)\)
Trong mp (ABCD), gọi O là giao điểm AC và BD
\(\left\{{}\begin{matrix}O\in AC\in\left(SAC\right)\\O\in BD\in\left(SBD\right)\end{matrix}\right.\)
\(\Rightarrow O\in\left(SAC\right)\cap\left(SBD\right)\)
\(\Rightarrow SO=\left(SAC\right)\cap\left(SBD\right)\)
b.
\(S\in\left(SAC\right)\cap\left(SBD\right)\)
Trong mp (ABCD), kéo dài AD và BC cắt nhau tại E
\(\left\{{}\begin{matrix}E\in AD\in\left(SAD\right)\\E\in BC\in\left(SBC\right)\end{matrix}\right.\)
\(\Rightarrow E\in\left(SAD\right)\cap\left(SBC\right)\)
\(\Rightarrow SE=\left(SAC\right)\cap\left(SBC\right)\)
c.
\(\left\{{}\begin{matrix}O\in BD\in\left(BDM\right)\\O\in SC\in\left(SAC\right)\end{matrix}\right.\)
\(\Rightarrow O\in\left(BDM\right)\cap\left(SAC\right)\)
\(\left\{{}\begin{matrix}M\in\left(BDM\right)\\M\in SA\in\left(SAC\right)\end{matrix}\right.\)
\(\Rightarrow M\in\left(BDM\right)\cap\left(SAC\right)\)
\(\Rightarrow OM=\left(BDM\right)\cap\left(SAC\right)\)