Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: \(\Leftrightarrow\dfrac{-3x^2+36x+12}{3\left(x+4\right)\left(x-1\right)}=\dfrac{36\left(x-1\right)}{3\left(x+4\right)\left(x-1\right)}+\dfrac{12\left(x+4\right)}{3\left(x-1\right)\left(x+4\right)}\)
\(\Leftrightarrow-3x^2+36x+12=36x-36+12x+48\)
\(\Leftrightarrow-3x^2+36x+12-48x-12=0\)
\(\Leftrightarrow3x\left(x+4\right)=0\)
=>x=0(nhận) hoặc x=-4(loại)

a: \(\Leftrightarrow x^2-4-4x^2-4x-1-2x+3x^2=0\)
=>-6x-5=0
=>-6x=5
hay x=-5/6
b: \(\Leftrightarrow2x^3+8x^2+8x-8x^2-2x^3+16=0\)
=>8x+16=0
hay x=-2
c: \(\Leftrightarrow x^3-6x^2+12x-8+9x^2-1-x^3-3x^2-3x-1=0\)
=>9x-10=0
hay x=10/9
d: \(\Leftrightarrow10x-15-20x+28=19-2x^2-4x-2\)
\(\Leftrightarrow-10x+13+2x^2+4x-17=0\)
\(\Leftrightarrow2x^2-6x-4=0\)
\(\Leftrightarrow x^2-3x-2=0\)
\(\text{Δ}=\left(-3\right)^2-4\cdot1\cdot\left(-2\right)=9+8=17>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{3-\sqrt{17}}{2}\\x_2=\dfrac{3+\sqrt{17}}{2}\end{matrix}\right.\)

a) Ta có: (5x-1)(x-3)<0
nên 5x-1 và x-3 trái dấu
Trường hợp 1:
\(\left\{{}\begin{matrix}5x-1>0\\x-3< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>\dfrac{1}{5}\\x< 3\end{matrix}\right.\Leftrightarrow\dfrac{1}{5}< x< 3\)
Trường hợp 2:
\(\left\{{}\begin{matrix}5x-1< 0\\x-3>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x< \dfrac{1}{5}\\x>3\end{matrix}\right.\Leftrightarrow loại\)
Vậy: S={x|\(\dfrac{1}{5}< x< 3\)}

a. \(\dfrac{-3}{x^2-9}+\dfrac{5}{3-x}=\dfrac{2}{x+3}\)
<=> \(\dfrac{-3}{x^2-9}+\dfrac{-5}{x-3}=\dfrac{2}{x+3}\)
<=> \(\dfrac{-3}{x^2-9}+\dfrac{-5\left(x+3\right)}{x^2-9}=\dfrac{2\left(x-3\right)}{x^2-9}\)
<=> \(-3+\left(-5\right)\left(x+3\right)=2\left(x-3\right)\)
<=> -3 + (-5x) + (-15) = 2x - 6
<=> -5x -2x = 15 - 6 + 3
<=> -7x = 12
<=> x = \(\dfrac{-12}{7}\)
Vậy ........
b. \(\left|x+5\right|=2x-1\)
Nếu x \(\ge\) -5 => \(\left|x+5\right|\) = x + 5
Nếu x < -5 => \(\left|x+5\right|\) = -(x + 5)
TH1: Nếu x \(\ge\) -5
<=> x + 5 = 2x - 1
<=> x - 2x = -1 - 5
<=> -x = -6
<=> x = 6
TH2: Nếu x < -5
<=> -(x + 5) = 2x - 1
<=> -x - 5 = 2x - 1
<=> -5 + 1 = 2x + x
<=> -4 = 3x
<=> x = \(\dfrac{-4}{3}\)
Vậy .........
c. Bạn tự giải câu này nhé (có thể tách các hạng tử rồi tính)

b: =>1/4x+4/5-x-5=1/3x+1-1/2x+1
=>-3/4x+1/6x=2+5-4/5=24/5
=>x=-288/35
c: =>6x^2+3x-30x-15=6x^2+10x-21x-35
=>-27x-15=-11x-35
=>-16x=-20
=>x=5/4

\(\text{2x - (x - 3)(5 - x) = (x+4)}^2.\)
\(\Leftrightarrow2x-\left(5x-x^2-15+3x\right)=x^2+8x+16.\)
\(\Leftrightarrow2x-5x+x^2+15-3x-x^2-8x-16=0.\)
\(\Leftrightarrow-14x-1=0.\Leftrightarrow x=\dfrac{-1}{14}.\)
\(\text{(4x + 1)(x - 2) + 25 = (2x+3)}^2-4x.\)
\(\Leftrightarrow4x^2-8x+x-2+25=4x^2+12x+9-4x.\)
\(\Leftrightarrow-15x+14=0.\Leftrightarrow x=\dfrac{14}{15}.\)

Bài 1:
a.
$(4x^2+4x+1)-x^2=0$
$\Leftrightarrow (2x+1)^2-x^2=0$
$\Leftrightarrow (2x+1-x)(2x+1+x)=0$
$\Leftrightarrow (x+1)(3x+1)=0$
$\Rightarrow x+1=0$ hoặc $3x+1=0$
$\Rightarrow x=-1$ hoặc $x=-\frac{1}{3}$
b.
$x^2-2x+1=4$
$\Leftrightarrow (x-1)^2=2^2$
$\Leftrightarrow (x-1)^2-2^2=0$
$\Leftrightarrow (x-1-2)(x-1+2)=0$
$\Leftrightarrow (x-3)(x+1)=0$
$\Leftrightarrow x-3=0$ hoặc $x+1=0$
$\Leftrightarrow x=3$ hoặc $x=-1$
c.
$x^2-5x+6=0$
$\Leftrightarrow (x^2-2x)-(3x-6)=0$
$\Leftrightarrow x(x-2)-3(x-2)=0$
$\Leftrightarrow (x-2)(x-3)=0$
$\Leftrightarrow x-2=0$ hoặc $x-3=0$
$\Leftrightarrow x=2$ hoặc $x=3$
2c.
ĐKXĐ: $x\neq 0$
PT $\Leftrightarrow x-\frac{6}{x}=x+\frac{3}{2}$
$\Leftrightarrow -\frac{6}{x}=\frac{3}{2}$
$\Leftrightarrow x=-4$ (tm)
2d.
ĐKXĐ: $x\neq 2$
PT $\Leftrightarrow \frac{1+3(x-2)}{x-2}=\frac{3-x}{x-2}$
$\Leftrightarrow \frac{3x-5}{x-2}=\frac{3-x}{x-2}$
$\Rightarrow 3x-5=3-x$
$\Leftrightarrow 4x=8$
$\Leftrightarrow x=2$ (không tm)
Vậy pt vô nghiệm.

a) 5(x-1)(x+1)=5x^2+3x-2
<=> (5x-5)(x+1) = (x+1)(5x-2)
<=> (x+1)(5x-5) - (x+1)(5x-2)=0
<=> (x+1)(5x-5-5x+2)=0
<=> (x+1).(-3)=0
<=> x+1=0<=> x=-1

a) \(\left(x-2\right)^2=\left(x-4\right)\left(x+4\right)\)
\(\Leftrightarrow x^2-4x+4-x^2+16=0\)
\(\Leftrightarrow20-4x=0\)
\(\Leftrightarrow4x=20\)
\(\Leftrightarrow x=5\)
Vậy S = {5}
b) ĐKXĐ: \(x\ne0;x\ne-2\)
\(\dfrac{x+2}{x}=\dfrac{\left(x+1\right)\left(x+4\right)}{x^2+2x}+\dfrac{x}{x+2}\)
\(\Leftrightarrow\dfrac{x+2}{x}=\dfrac{x^2+4x+x+4+x^2}{x\left(x+2\right)}\)
\(\Leftrightarrow\dfrac{x+2}{x}=\dfrac{2x^2+5x+4}{x\left(x+2\right)}\)
\(\Rightarrow x\left(x+2\right)^2=x\left(2x^2+5x+4\right)\)
\(\Leftrightarrow x^3+4x^2+4x=2x^3+5x^2+4x\)
\(\Leftrightarrow x^3+x^2=0\)
\(\Leftrightarrow x^2\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2=0\\x+1=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\left(loại\right)\\x=-1\left(TM\right)\end{matrix}\right.\)
Vậy S = {-1}
c) Câu này mình không chắc về đề lắm! Bạn dùng ô chữ M bị ngược để viết lại đề nhé!
a) Ta có: \(\left(x-2\right)^2=\left(x-4\right)\left(x+4\right)\)
\(\Leftrightarrow x^2-4x+4=x^2-16\)
\(\Leftrightarrow x^2-4x+4-x^2+16=0\)
\(\Leftrightarrow-4x+20=0\)
\(\Leftrightarrow-4x=-20\)
hay x=5
Vậy: S={5}

a) \(2\chi-3=3\left(\chi+1\right)\)
\(\Leftrightarrow2\chi-3=3\chi+3\)
\(\Leftrightarrow2\chi-3\chi=3+3\)
\(\Leftrightarrow\chi=-6\)
Vậy phương trình có tập nghiệm S= \(\left\{-6\right\}\)
\(3\chi-3=2\left(\chi+1\right)\)
\(\Leftrightarrow3\chi-3=2\chi+2\)
\(\Leftrightarrow3\chi-2\chi=2+3\)
\(\Leftrightarrow\chi=5\)
Vậy phương trình có tập nghiệm S= \(\left\{5\right\}\)
b) \(\left(3\chi+2\right)\left(4\chi-5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3\chi+2=0\\4\chi-5=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3\chi=-2\\4\chi=5\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\chi=\dfrac{-2}{3}\\\chi=\dfrac{5}{4}\end{matrix}\right.\)
Vậy phương trình có tập nghiệm S= \(\left\{\dfrac{-2}{3};\dfrac{5}{4}\right\}\)
\(\left(3\chi+5\right)\left(4\chi-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3\chi+5=0\\4\chi-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3\chi=-5\\4\chi=2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\chi=\dfrac{-5}{3}\\\chi=\dfrac{1}{2}\end{matrix}\right.\)
Vậy phương trình có tập nghiệm S= \(\left\{\dfrac{-5}{3};\dfrac{1}{2}\right\}\)
c) \(\left|\chi-7\right|=2\chi+3\)
Trường hợp 1:
Nếu \(\chi-7\ge0\Leftrightarrow\chi\ge7\)
Khi đó:\(\left|\chi-7\right|=2\chi+3\)
\(\Leftrightarrow\chi-7=2\chi+3\)
\(\Leftrightarrow\chi-2\chi=3+7\)
\(\Leftrightarrow\chi=-10\) (KTMĐK)
Trường hợp 2:
Nếu \(\chi-7\le0\Leftrightarrow\chi\le7\)
Khi đó: \(\left|\chi-7\right|=2\chi+3\)
\(\Leftrightarrow-\chi+7=2\chi+3\)
\(\Leftrightarrow-\chi-2\chi=3-7\)
\(\Leftrightarrow-3\chi=-4\)
\(\Leftrightarrow\chi=\dfrac{4}{3}\)(TMĐK)
Vậy phương trình có tập nghiệm S=\(\left\{\dfrac{4}{3}\right\}\)
\(\left|\chi-4\right|=5-3\chi\)
Trường hợp 1:
Nếu \(\chi-4\ge0\Leftrightarrow\chi\ge4\)
Khi đó: \(\left|\chi-4\right|=5-3\chi\)
\(\Leftrightarrow\chi-4=5-3\chi\)
\(\Leftrightarrow\chi+3\chi=5+4\)
\(\Leftrightarrow4\chi=9\)
\(\Leftrightarrow\chi=\dfrac{9}{4}\)(KTMĐK)
Trường hợp 2: Nếu \(\chi-4\le0\Leftrightarrow\chi\le4\)
Khi đó: \(\left|\chi-4\right|=5-3\chi\)
\(\Leftrightarrow-\chi+4=5-3\chi\)
\(\Leftrightarrow-\chi+3\chi=5-4\)
\(\Leftrightarrow2\chi=1\)
\(\Leftrightarrow\chi=\dfrac{1}{2}\)(TMĐK)
Vậy phương trình có tập nghiệm S=\(\left\{\dfrac{1}{2}\right\}\)
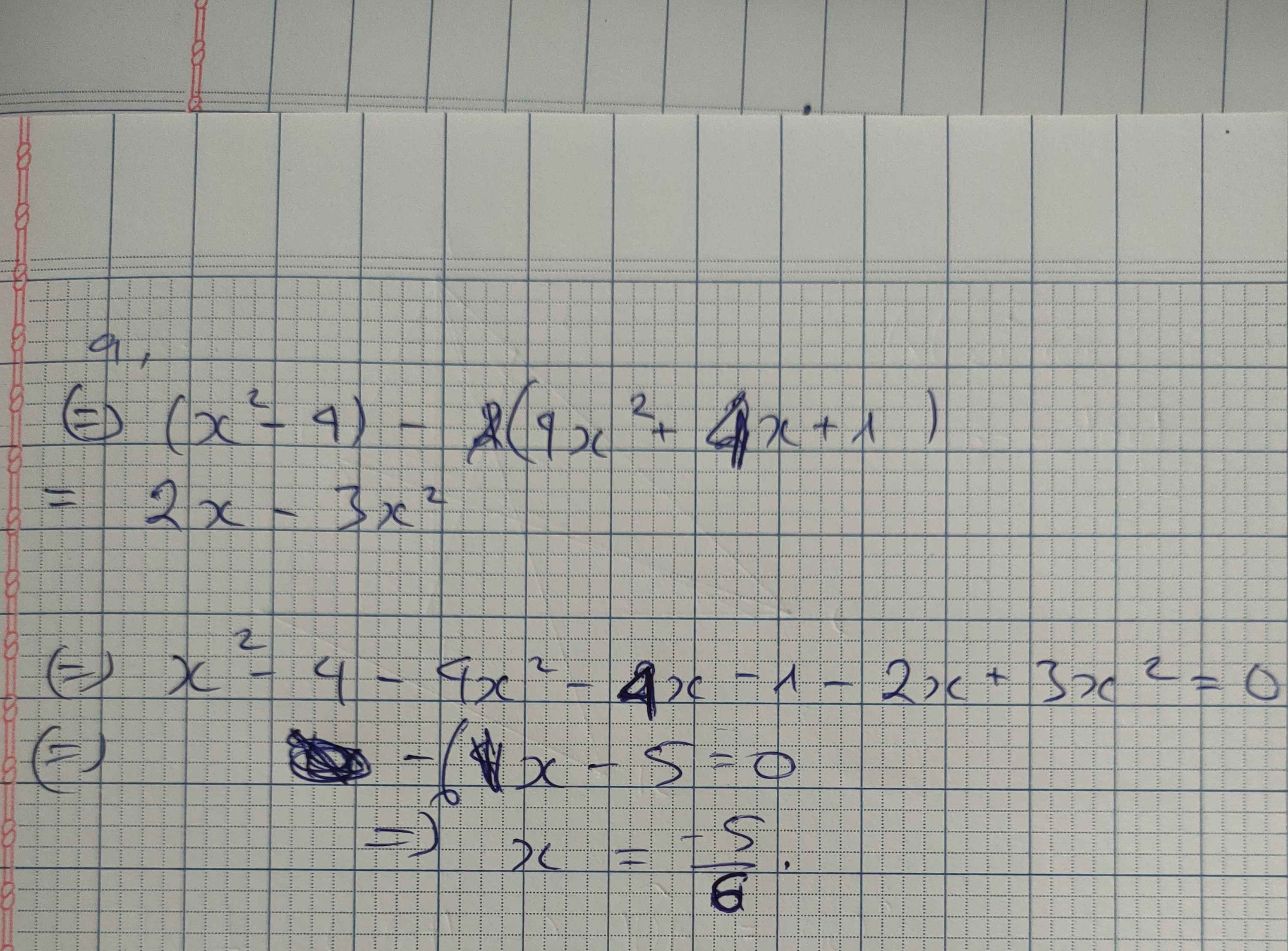
a) |x-3| + |5-x|=4
x-3+5-x=4
x-x=3-5+4
0=2
vậy tập nghiệm của phương trình: S=vô nghệm
b) |x-1| +|x-2|+3|x-4|=11
x-1+x-2+3*(x-4)=11
x-1+x-2+3x-12=11
x+x+3x=1+2+12+11
5x=26
x=\(\frac{26}{15}\)
vậy tập nghiệm của phương trình: S=\(\frac{26}{15}\)
c)|x-1|+|x-2|+|x-3|+|x-4|+30=5x
x-1+x-2+x-3+x-4+30=5x
x+x+x+x-5x=1+2+3+4-30
-x=-20
x=20
vậy tập nghiệm của phương trình: S={20}