K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
GB
28 tháng 10 2021
Tham khảo:
1. Sử dụng hai góc kề bù có ba điểm nằm trên hai cạnh là hai tia đối nhau.
2. Ba điểm cùng thuộc một tia hoặc một một đường thẳng
3. Trong ba đoạn thẳng nối hai trong ba điểm có một đoạn thẳng bằng tổng hai đoạn thẳng kia.
4. Hai đoạn thẳng cùng đi qua hai trong ba điểm ấy cùng song song với đường thẳng thứ ba.
5. Hai đường thẳng cùng đi qua hai trong ba điểm ấy cùng vuông góc với đường thẳng thứ ba.
6. Đường thẳng cùng đi qua hai trong ba điểm ấy có chứa điểm thứ ba.
7. Sử dụng tính chất đường phân giác của một góc, tính chất đường trung trực của đoạn thẳng, tính chất ba đường cao trong tam giác .
8. Sử dụng tính chất hình bình hành.
9. Sử dụng tính chất góc nội tiếp đường tròn.
10. Sử dụng góc bằng nhau đối đỉnh
11. Sử dụng trung điểm các cạnh bên, các đường chéo của hình thang thẳng hàng
12. Chứng minh phản chứng
13. Sử dụng diện tích tam giác tạo bởi ba điểm bằng 0
14. Sử dụng sự đồng qui của các đường thẳng.
2 tháng 10 2019
\(\frac{1}{27}\)x3+\(\frac{1}{125}\)y3
=(\(\frac{1}{3}\)x)3+(\(\frac{1}{5}\)y)3
=(\(\frac{1}{3}\)x+\(\frac{1}{5}\)y)[(\(\frac{1}{3}\)x)2-\(\frac{1}{3}\)x.\(\frac{1}{5}\)y+(\(\frac{1}{5}\)y)2]
=(\(\frac{1}{3}\)x+\(\frac{1}{5}\)y)(\(\frac{1}{9}\)x2-\(\frac{1}{15}\)xy+\(\frac{1}{25}\)y2)
17 tháng 11 2021
\(\left\{{}\begin{matrix}AD=BC\\\widehat{EHG}=\widehat{FGE}\\\widehat{EMH}=\widehat{ENG}=90^0\end{matrix}\right.\Rightarrow\Delta EMH=\Delta ENF\\ \Rightarrow EM=EN=6\left(cm\right)\)
R
23 tháng 11 2021
1)\(\dfrac{4x-5}{x-1}=2+\dfrac{x}{x-1}\)
⇔\(\dfrac{4x-5}{x-1}=\dfrac{2\left(x-1\right)}{x-1}+\dfrac{x}{x-1}\)
⇔\(4x-5=2\left(x-1\right)+x\)
⇔\(4x-5=2x-2+x\)
⇔\(4x-5-2x+2-x=0\)
⇔\(x-3=0\)
⇔\(x=3\)
2)\(\dfrac{7}{x+2}=\dfrac{3}{x-5}\)
⇔\(7\left(x-5\right)=3\left(x+2\right)\)
⇔\(7x-35=3x+6\)
⇔\(7x-35-3x-6=0\)
⇔\(4x-41=0\)
⇔\(4x=41\)
⇔\(x=\dfrac{41}{4}\)
PC
2
23 tháng 7 2021
Bài 1:
a) Ta có: \(2\left(3-4x\right)=10-\left(2x-5\right)\)
\(\Leftrightarrow6-8x-10+2x-5=0\)
\(\Leftrightarrow-6x+11=0\)
\(\Leftrightarrow-6x=-11\)
hay \(x=\dfrac{11}{6}\)
b) Ta có: \(3\left(2-4x\right)=11-\left(3x-1\right)\)
\(\Leftrightarrow6-12x-11+3x-1=0\)
\(\Leftrightarrow-9x-6=0\)
\(\Leftrightarrow-9x=6\)
hay \(x=-\dfrac{2}{3}\)
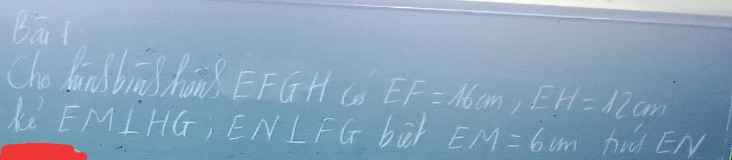
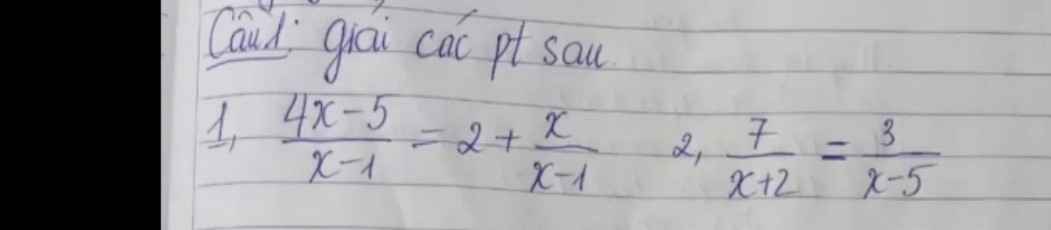
2)\(\dfrac{x+5}{3x-6}-\dfrac{1}{2}=\dfrac{2x-3}{2x-4}\)
⇔\(\dfrac{x+5}{3\left(x-2\right)}-\dfrac{1}{2}=\dfrac{2x-3}{2\left(x-2\right)}\)
⇔\(\dfrac{2\left(x+5\right)}{3.2\left(x-2\right)}-\dfrac{3\left(x-2\right)}{2.3\left(x-2\right)}=\dfrac{3\left(2x-3\right)}{2.3\left(x-2\right)}\)
⇔\(\dfrac{2x+10}{6\left(x-2\right)}-\dfrac{3x-6}{6\left(x-2\right)}=\dfrac{6x-9}{6\left(x-2\right)}\)
⇔\(2x+10-\left(3x-6\right)=6x-9\)
⇔\(2x+10-3x+6-6x+9=0\)
⇔\(-7x+25=0\)
⇔\(-7x=-25\)
⇔\(x=\dfrac{25}{7}\)
3)\(\dfrac{1}{x-1}-\dfrac{3x^2}{x^3-1}=\dfrac{2x}{x^2+x+1}\)
⇔\(\dfrac{1}{x-1}-\dfrac{3x^2}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{2x}{x^2+x+1}\)
⇔\(\dfrac{x^2+x+1}{\left(x-1\right)\left(x^2+x+1\right)}-\dfrac{3x^2}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{2x\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\)
⇔\(x^2+x+1-3x^2=2x^2-2x\)
⇔\(x^2+x+1-3x^2-2x^2+2x=0\)
⇔\(-4x^2+3x+1=0\)
⇔\(-\left(4x^2-3x-1\right)=0\)
⇔\(-\left(4x^2-4x+x-1\right)=0\)
⇔\(-\left[\left(4x^2-4x\right)+\left(x-1\right)\right]=0\)
⇔\(-\left[4x\left(x-1\right)+\left(x-1\right)\right]=0\)
⇔\(-\left[\left(x-1\right)\left(4x+1\right)\right]=0\)
⇔\(-\left(x-1\right)=0\) hay \(-\left(4x+1\right)=0\)
⇔\(-x+1=0\) hay \(-4x-1=0\)
⇔\(-x=-1\) hay \(-4x=1\)
⇔\(x=1\) hay \(x=-\dfrac{1}{4}\)