Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\sqrt{2023-\sqrt{x}}=2023-x\left(ĐK:x\ge0\right)\)
Đặt \(t=\sqrt{x}\left(t\le2023\right)\)
Pt trở thành : \(\sqrt{2023-t}=2023-t^2\)
\(\Leftrightarrow2023-t=\left(2023-t^2\right)^2\)
\(\Leftrightarrow t^4-4046t+4092529=2023-t\)
\(\Leftrightarrow t^4-4045+4090506=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=2023\left(n\right)\\t=2022\left(n\right)\end{matrix}\right.\)
+) Với \(t=2023\Rightarrow x^2=2023\Rightarrow x=\pm17\sqrt{7}\)
+) Với \(t=2022\Rightarrow x^2=2022\Leftrightarrow x=\pm\sqrt{2022}\)
Vì \(x\ge0\) \(\Rightarrow x\in\left\{17\sqrt{7};\sqrt{2022}\right\}\)
Vậy \(S=\left\{17\sqrt{7};\sqrt{2022}\right\}\)

\(a,ĐK:x\in R\)
\(b,ĐK:\dfrac{-7}{8-10x}\ge0\Leftrightarrow8-10x< 0\left(-7< 0\right)\Leftrightarrow x>\dfrac{4}{5}\)
\(c,ĐK:\dfrac{24-6x}{-7}\ge0\Leftrightarrow24-6x\le0\left(-7< 0\right)\Leftrightarrow x\ge4\)

Điều kiện xác định
\(\hept{\begin{cases}2-x^2+2x\ge0\\-x^2-6x-8\ge0\end{cases}}\Leftrightarrow\hept{\begin{cases}-0,73\le x\le2,73\\-4\le x\le-2\end{cases}}\)
=> Tập xác định là tập rỗng
Vậy pt vô nghiệm

\(\sqrt{\dfrac{72x}{128}}=\dfrac{3}{4}\)
\(\Leftrightarrow x\cdot\dfrac{9}{16}=\dfrac{9}{16}\)
hay x=1

\(\sqrt{x^2-9}-3\sqrt{x-3}=0\left(đk:x\ge3\right)\)
\(\Leftrightarrow\sqrt{\left(x-3\right)\left(x+3\right)}-3\sqrt{x-3}=0\)
\(\Leftrightarrow\sqrt{x-3}\left(\sqrt{x+3}-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x-3}=0\\\sqrt{x+3}=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x+3=9\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=3\left(tm\right)\\x=6\left(tm\right)\end{matrix}\right.\)
\(ĐK:x\le-3;x\ge3\\ PT\Leftrightarrow\sqrt{x-3}\left(\sqrt{x+3}-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-3=0\\\sqrt{x+3}=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x+3=9\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\left(tm\right)\\x=6\left(tm\right)\end{matrix}\right.\)

1.
x + \(\sqrt{1-x^2}\) = 1
ĐK: -1 <= x <= 1
<=> \(\sqrt{1-x^2}\)= 1 - x
Vì 1 - x >= 0 nên ta có thể bình phương 2 vế
<=> 1 - x2 = (1 - x)2
<=> 1 - x2 = 1 - 2x + x2
<=> 2x2 - 2x = 0
<=>
x = 0
x = 1
2.
Hệ tương đương
\(\hept{\begin{cases}6\left(x+y\right)=5xy\\\frac{4y-3x}{xy}=1\end{cases}}\)
<=>
\(\hept{\begin{cases}6\left(x+y\right)=5xy\\4y-3x=xy\end{cases}}\)
<=>
\(\hept{\begin{cases}6\left(x+y\right)=5\left(4y-3x\right)\\4y-3x=xy\end{cases}}\)
<=>
\(\hept{\begin{cases}14y-21x=0\\4y-3x=xy\end{cases}}\)
<=>
\(\hept{\begin{cases}14y-21x=0\\y=\frac{3x}{4-x}\end{cases}}\)
Thay y = \(\frac{3x}{4-x}\)Vào PT trên
=> \(\frac{42x}{4-x}\)= 21x
<=> 42x = 21x(4 - x)
<=> 2x = x(4 - x)
<=> x2 - 2x = 0
x = 0 (Loại vi x khác 0)
x = 2, => y = 3
Vậy, Nghiêm của hệ PT:
x = 2
y = 3

\(\sqrt{x-2}-\sqrt{4-x}=0\)
\(\Leftrightarrow\sqrt{x-2}=\sqrt{4-x}\)
\(\Leftrightarrow\left(\sqrt{x-2}\right)^2=\left(\sqrt{4-x}\right)^2\)
\(\Leftrightarrow x-2=4-x\)
\(\Leftrightarrow2x=4+2\)
\(\Leftrightarrow2x=6\)
\(\Leftrightarrow x=3\)
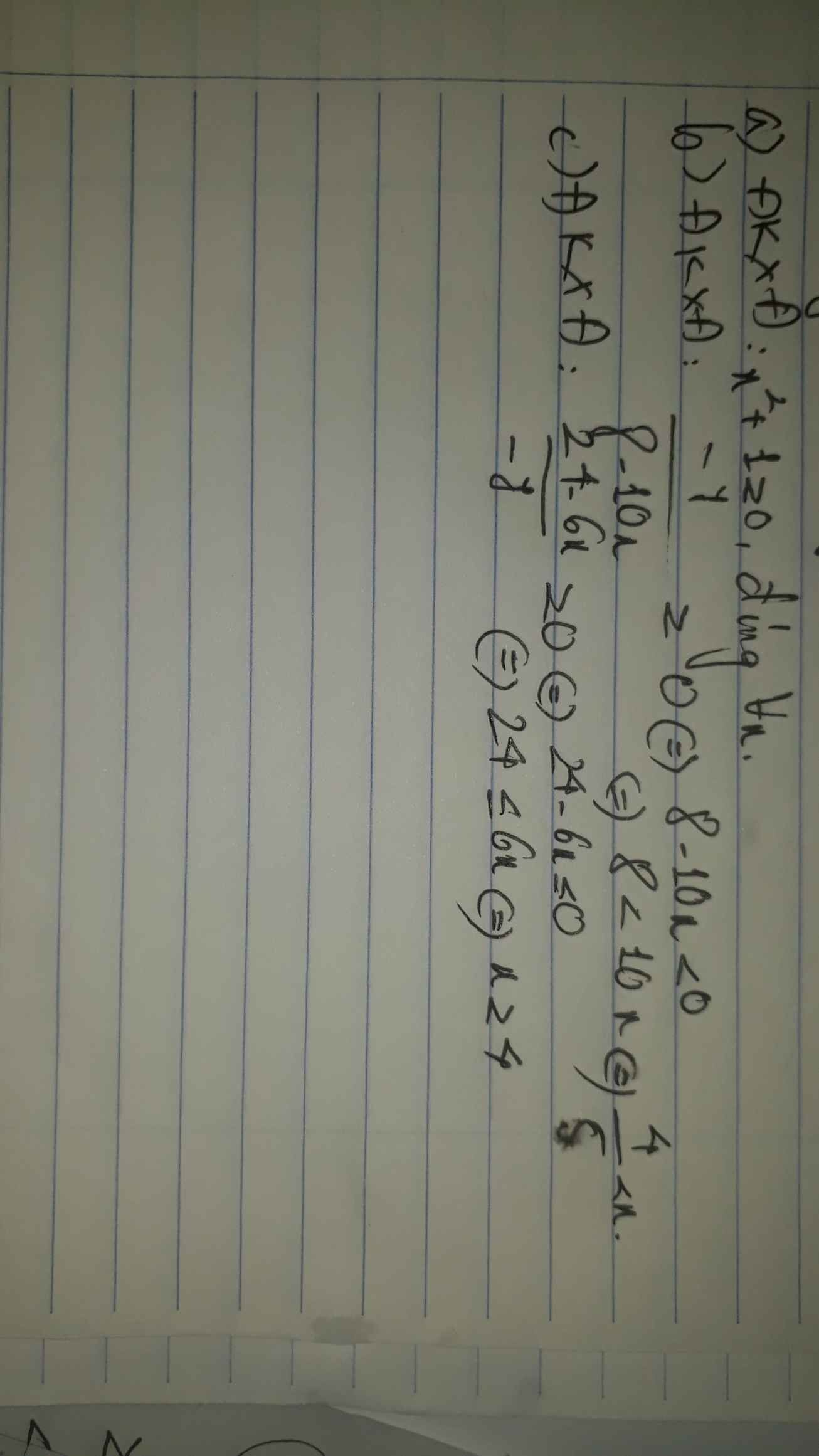
x,y là số nguyên tố đúng ko?
ĐK \(-1\le x\le7\)
Ta có \(VT=x^2-6x+13=\left(x-3\right)^2+4\ge4\)(1)
\(2VP=\sqrt{4\left(7-x\right)}+\sqrt{4\left(x+1\right)}\le\frac{4+7-x+4+1+x}{2}=8\)
=> \(VP\le4\)(2)
Từ (1);(2)
=> đẳng thức xảy ra khi x=3(tm ĐKXĐ)
Vậy x=3