Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
thay x=1/2 vào phương trình, ta được:
(1/2+a)/(a-1/2)+(1/2-a)/(a+1/2) =(a.(5a+10))/(a2-(1/2)2) (a khác +- 1/2)
<=>((1/2+a)2)/(a2-(1/2)2) +((1/2-a).(a-1/2))/(a2-(1/2)2) -(a.(5a+10))/(a2-(1/2)2) =0
<=> a2+a+1/4+a/2-a2-1/4+a/2-5a2+a=0
<=>2a+2a/2-5a2 =0
<=>4a+2a-10a2=0
<=>6a-10a2=0
<=> 2a(3-5a)=0
<=>a=0 hoặc a=3/5(tmđk)
vậy a=0 hoặc a=3/5
1: Hai phương trình gọi là tương đương khi chúng có chung tập nghiệm
2: Phương trình bậc nhất một ẩn là phương trình có dạng ax+b=0(a<>0), với a,b là các số thực
1: Hai phương trình gọi là tương đương khi chúng có chung tập nghiệm
2: Phương trình bậc nhất một ẩn là phương trình có dạng ax+b=0(a<>0), với a,b là các số thực
![[CHUẨN NHẤT] Thế nào là hai phương trình tương đương](https://api.toploigiai.vn/storage/uploads/the-nao-la-hai-phuong-trinh-tuong-duong_1)
![[CHUẨN NHẤT] Thế nào là hai phương trình tương đương (ảnh 2)](https://api.toploigiai.vn/storage/uploads/the-nao-la-hai-phuong-trinh-tuong-duong_2)
+) Cách làm của bạn Sơn sai vì chưa đặt điều kiện xác định cho phương trình đã nhân cả hai vế với ( x- 5).
+) Cách làm của bạn Hà sai vì chưa đặt điều kiện xác định cho phương trình đã rút gọn cả hai vế cho biểu thức (x- 5) phụ thuộc biến x.
+) Cách giải đúng
Điều kiện xác định:
Ta có:
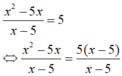
Suy ra: x2 – 5x = 5( x- 5)
x( x- 5) – 5(x – 5) = 0
( x- 5).( x- 5) =0
(x - 5)2 = 0
x – 5= 0
x = 5 ( không thỏa mãn ĐKXĐ).
Vậy phương trình đã cho vô nghiệm.
mình tìm không tháy bạn ơi ~ chủ yếu là mình nhờ mấy bạn từng học qua rồi chỉ giúp những dạng chủ yếu,mẹo vặt các loại đấy bạn !! không phải mình tìm đề đâu ~~`
gọi hs nam là a , hs nữ là b thì ta có
a+b=45
a-b=3 <=$ a=b+3
=> b+3+b=45
<=> 2b=45-3
<=> 2b=42
<=> b= 21 (hs nữ)
a+21=45
=> a=24 (hs nam)
Bài 1
Gọi số học sinh lớp 8A là x (học sinh) ĐK: x ∈ N* và x < 80
Số học sinh lớp 8B là 80 - x(học sinh)
Số sách lớp 8A ủng hộ là 2x (quyển)
Số sách lớp 8B ủng hộ là 3(80 - x) (quyển)
Theo bài ta có phương trình:
<=>2x + 3(80 - x) = 198
<=>2x + 248 - 3x = 198
x = 42 (thoả mãn điều kiện) Vậy số học sinh lớp 8A là 42 học sinh,số học sinh lớp 8B là 38 học sinh.
Bài 2
Gọi độ dài quãng đường AB là x (km) (ĐK: x > 0)
Thời gian lúc đi là: x/35 (giờ), thời gian lúc về là : x/42 (giờ).
Theo bài ra ta có phương trình: x/35 - x/42 = 1/2
Giải phương trình được x = 105, thoả mãn điều kiện của ẩn. Trả lời : Vậy độ dài quãng đường AB là 105 km.
Hok tốt ^^
Bài 1: Gọi x (h/s) là số h/s của lớp 8A (0 < x < 80 ). Số h/s của lớp 8D là: 80 - x
Số cách lớp 8a ủng hộ là 2x (quyển); số sách lớp 8D ủng hộ là 3(80 - x) (quyển)
Theo đề bài 2 lớp góp đc 198 nên ta có phương trình: 2x +3(80 - x) = 198
<=> 2x + 240 - 3x = 198 => x = 42 (h/s) (TMĐK) => Số h/s lớp 8A là: 42 h/s
Số h/s lớp 8D là: 80 - x = 80 - 24 = 56 (h/s)
Bài 2: Gọi t(h) là thời gian đi (t > 0,5) - quãng đường AB (tính theo lúc đi) 35t
- quãng đường AB (tính theo lúc về) 42(t - 0,5)
Ta có phương trình: 35t = 42(t - 0,5) giải phương trình: 35t = 42(t-0,5)
<=> 35t = 42t - 21 <=> -7t = -21 <=> t = 3
=> Quãng đường AB dài là: 35.3 = 105 (km)
Gọi số cần là ab(a+b=16).
Vì khi đổi chỗ 2 chữ số của nó cho nhau thì được 1 số kém số ban đầu là 18.
Do đó: \(ba-ab=18\)
\(\Rightarrow10b+a-10a-b=18\)
\(\Rightarrow9b-9a=18\)
\(\Rightarrow9\left(b-a\right)=18\)
\(\Rightarrow b-a=2\)
Mà \(a+b=16\)
\(\Rightarrow a=\left(16-2\right):2=7\)
\(\Rightarrow b=a+2=7+2=9\)
Vậy số cần tìm là \(79\)
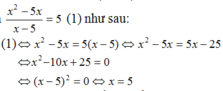
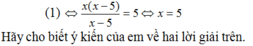
⇔ 9s = 7(90 - s) + 126
⇔ 9s = 756 - 7s
⇔ 16s = 756
⇔ s = 47,25(km)
Thời gian để hai xe gặp nhau từ lúc xe máy khởi hành là:
So sánh hai cách chọn ẩn, cách đầu tiên (chọn ẩn là thời gian từ lúc xe máy khởi hành đến lúc hai xe gặp nhau) cho cách giải ngắn gọn hơn vì phương trình đơn giản hơn.