Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)\(\dfrac{x+1}{x^2+x+1}-\dfrac{x-1}{x^2-x+1}=\dfrac{3}{x\left(x^4+x^2+1\right)}\left(1\right)\)
ĐK:\(x\ne0\)
\(\left(1\right)\Leftrightarrow\dfrac{x^3+1-\left(x^3-1\right)}{\left(x^2+1+x\right)\left(x^2+1-x\right)}=\dfrac{3}{x\left(x^4+x^2+1\right)}\\ \Leftrightarrow\dfrac{2}{\left(x^2+1\right)^2-x^2}=\dfrac{3}{x\left(x^4+x^2+1\right)}\\ \Leftrightarrow\dfrac{2x-3}{x\left(x^4+x^2+1\right)}=0\Rightarrow2x-3=0\Leftrightarrow x=\dfrac{3}{2}\left(TM\right)\)
\(\dfrac{9-x}{2009}+\dfrac{11-x}{2011}=2\Leftrightarrow\left(\dfrac{9-x}{2009}-1\right)+\left(\dfrac{11-x}{2011}-1\right)=0\Leftrightarrow\dfrac{-2000-x}{2009}+\dfrac{-2000-x}{2011}=0\\ \Leftrightarrow\left(-2000-x\right)\left(\dfrac{1}{2009}+\dfrac{1}{2011}\right)=0\Rightarrow x=-2000\)

\(\dfrac{123}{456}\cdot\left(\dfrac{2010}{2011}-\dfrac{2011}{2010}\right)-\left(\dfrac{2009}{2010}-\dfrac{1}{2011}\right):\dfrac{456}{123}\)
\(=\dfrac{123}{456}\cdot\left(\dfrac{2010}{2011}-\dfrac{2011}{2010}\right)-\left(\dfrac{2009}{2010}-\dfrac{1}{2011}\right)\cdot\dfrac{123}{456}\)
\(=\dfrac{123}{456}\left[\left(\dfrac{2010}{2011}-\dfrac{2011}{2010}\right)-\left(\dfrac{2009}{2010}-\dfrac{1}{2011}\right)\right]\)
\(=\dfrac{123}{456}\left(\dfrac{2010}{2011}-\dfrac{2011}{2010}-\dfrac{2009}{2010}+\dfrac{1}{2011}\right)\)
\(=\dfrac{123}{456}\left[\left(\dfrac{2010}{2011}+\dfrac{1}{2011}\right)-\left(\dfrac{2011}{2010}+\dfrac{2009}{2010}\right)\right]\)
\(=\dfrac{123}{456}\left(1-2\right)\)
\(=-\dfrac{123}{456}\)

1.
ĐK: \(x\ne7;x\ne-1;x\ne3\)
\(\dfrac{2x-5}{x^2-6x-7}\le\dfrac{1}{x-3}\left(1\right)\)
TH1: \(x< -1\)
\(\left(1\right)\Leftrightarrow\left(2x-5\right)\left(x-3\right)\ge x^2-6x-7\)
\(\Leftrightarrow2x^2-11x+15\ge x^2-6x-7\)
\(\Leftrightarrow x^2-5x+22\ge0\)
\(\Leftrightarrow\) Bất phương trình đúng với mọi \(x< -1\)
TH2: \(-1< x< 3\)
\(\left(1\right)\Leftrightarrow\left(3-x\right)\left(2x-5\right)\ge\left(7-x\right)\left(x+1\right)\)
\(\Leftrightarrow-2x^2+11x-15\ge-x^2+6x+7\)
\(\Leftrightarrow-x^2+5x-22\ge0\)
\(\Rightarrow\) vô nghiệm
TH3: \(3< x< 7\)
Khi đó \(\dfrac{2x-5}{x^2-6x-7}\le0\); \(\dfrac{1}{x-3}>0\)
\(\Rightarrow\) Bất phương trình đúng với mọi \(3< x< 7\)
TH4: \(x>7\)
\(\left(1\right)\Leftrightarrow\left(2x-5\right)\left(x-3\right)\le x^2-6x-7\)
\(\Leftrightarrow2x^2-11x+15\le x^2-6x-7\)
\(\Leftrightarrow x^2-5x+22\le0\)
\(\Rightarrow\) vô nghiệm
Vậy ...
Các bài kia tương tự, chứ giải ra mệt lắm.

a) \(\left(x+1\right)\left(x-1\right)\left(3x-6\right)>0\)
Lập bảng xét dấu ta được kết quả :
\(Bpt\Leftrightarrow\left[{}\begin{matrix}-1< x< 1\\x>2\end{matrix}\right.\)
b) \(\dfrac{x+3}{x-2}\le0\)
Lập bảng xét dấu ta được kết quả :
\(Bpt\Leftrightarrow-3\le x< 2\)
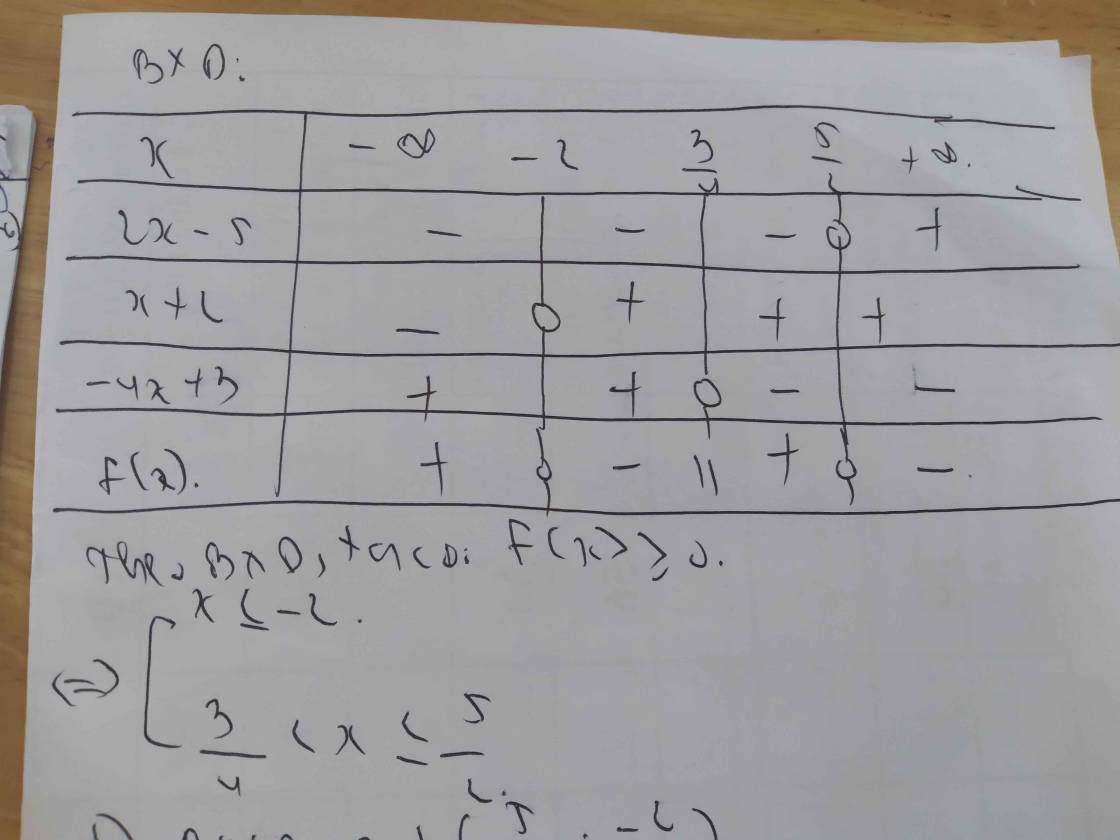
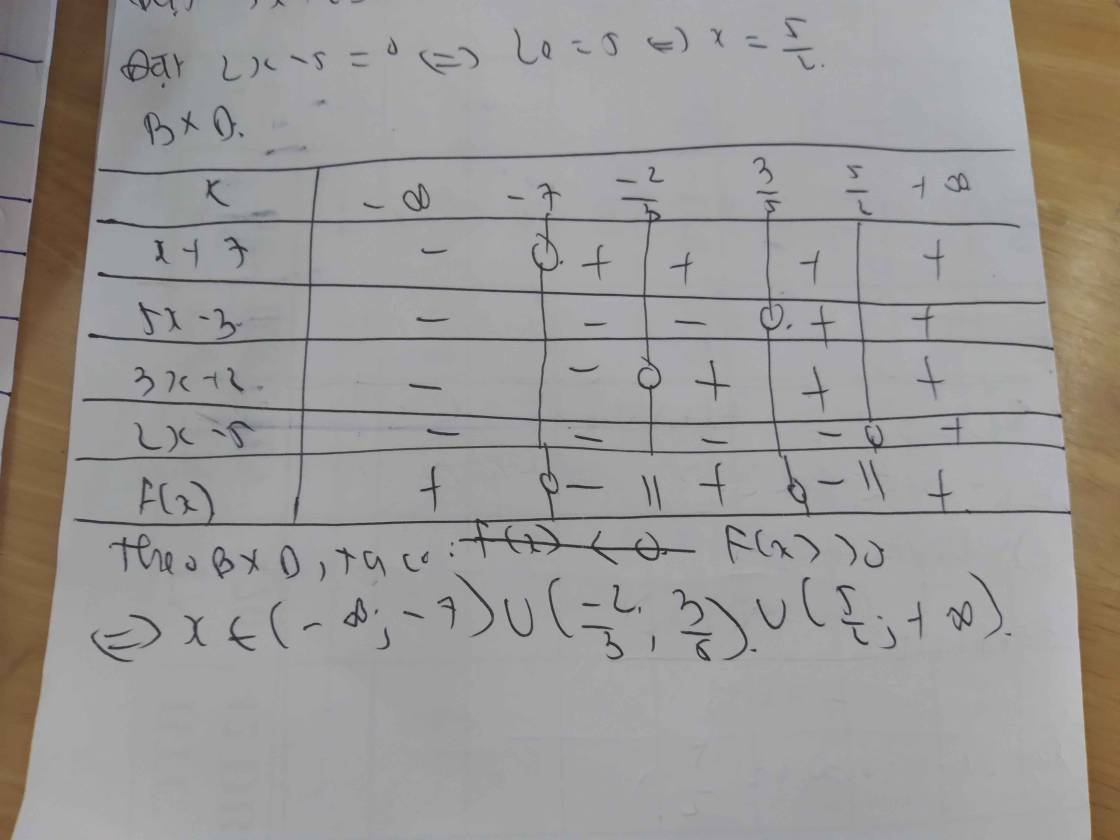
d) \(\dfrac{2x-5}{3x+2}< \dfrac{3x+2}{2x-5}\)
\(\Leftrightarrow\dfrac{2x-5}{3x+2}-\dfrac{3x+2}{2x-5}< 0\)
\(\Leftrightarrow\dfrac{\left(2x-5\right)^2-\left(3x+2\right)^2}{\left(3x+2\right)\left(2x-5\right)}< 0\)
\(\Leftrightarrow\dfrac{\left(2x-5+3x+2\right)\left(2x-5-3x-2\right)}{\left(3x+2\right)\left(2x-5\right)}< 0\)
\(\Leftrightarrow\dfrac{-\left(5x-3\right)\left(x+7\right)}{\left(3x+2\right)\left(2x-5\right)}< 0\)
Lập bảng xét dấu ta được kết quả :
\(Bpt\Leftrightarrow\left[{}\begin{matrix}-7< x< -\dfrac{2}{3}\\\dfrac{5}{3}< x< \dfrac{5}{2}\end{matrix}\right.\)

lời giải
a) \(\left\{{}\begin{matrix}-2x+\dfrac{3}{5}>\dfrac{2x-7}{3}\left(1\right)\\x-\dfrac{1}{2}< \dfrac{5\left(3x-1\right)}{2}\left(2\right)\end{matrix}\right.\)
(1)\(\Leftrightarrow\)
\(\dfrac{3}{5}+\dfrac{7}{3}>\left(\dfrac{2}{3}+2\right)x\)
\(\dfrac{44}{15}>\dfrac{8}{3}x\) \(\Rightarrow x< \dfrac{44.3}{15.8}=\dfrac{11}{5.2}=\dfrac{11}{10}\)
Nghiêm BPT(1) là \(x< \dfrac{11}{10}\)
(2) \(\Leftrightarrow2x-1< 15x-5\Rightarrow13x>4\Rightarrow x>\dfrac{4}{13}\)
Ta có: \(\dfrac{4}{13}< \dfrac{11}{10}\) => Nghiệm hệ (a) là \(\dfrac{4}{13}< x< \dfrac{11}{10}\)


1.
\(x^4-6x^2-12x-8=0\)
\(\Leftrightarrow x^4-2x^2+1-4x^2-12x-9=0\)
\(\Leftrightarrow\left(x^2-1\right)^2=\left(2x+3\right)^2\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-1=2x+3\\x^2-1=-2x-3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-2x-4=0\\x^2+2x+2=0\end{matrix}\right.\)
\(\Leftrightarrow x=1\pm\sqrt{5}\)
3.
ĐK: \(x\ge-9\)
\(x^4-x^3-8x^2+9x-9+\left(x^2-x+1\right)\sqrt{x+9}=0\)
\(\Leftrightarrow\left(x^2-x+1\right)\left(\sqrt{x+9}+x^2-9\right)=0\)
\(\Leftrightarrow\sqrt{x+9}+x^2-9=0\left(1\right)\)
Đặt \(\sqrt{x+9}=t\left(t\ge0\right)\Rightarrow9=t^2-x\)
\(\left(1\right)\Leftrightarrow t+x^2+x-t^2=0\)
\(\Leftrightarrow\left(x+t\right)\left(x-t+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-t\\x=t-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\sqrt{x+9}\\x=\sqrt{x+9}-1\end{matrix}\right.\)
\(\Leftrightarrow...\)

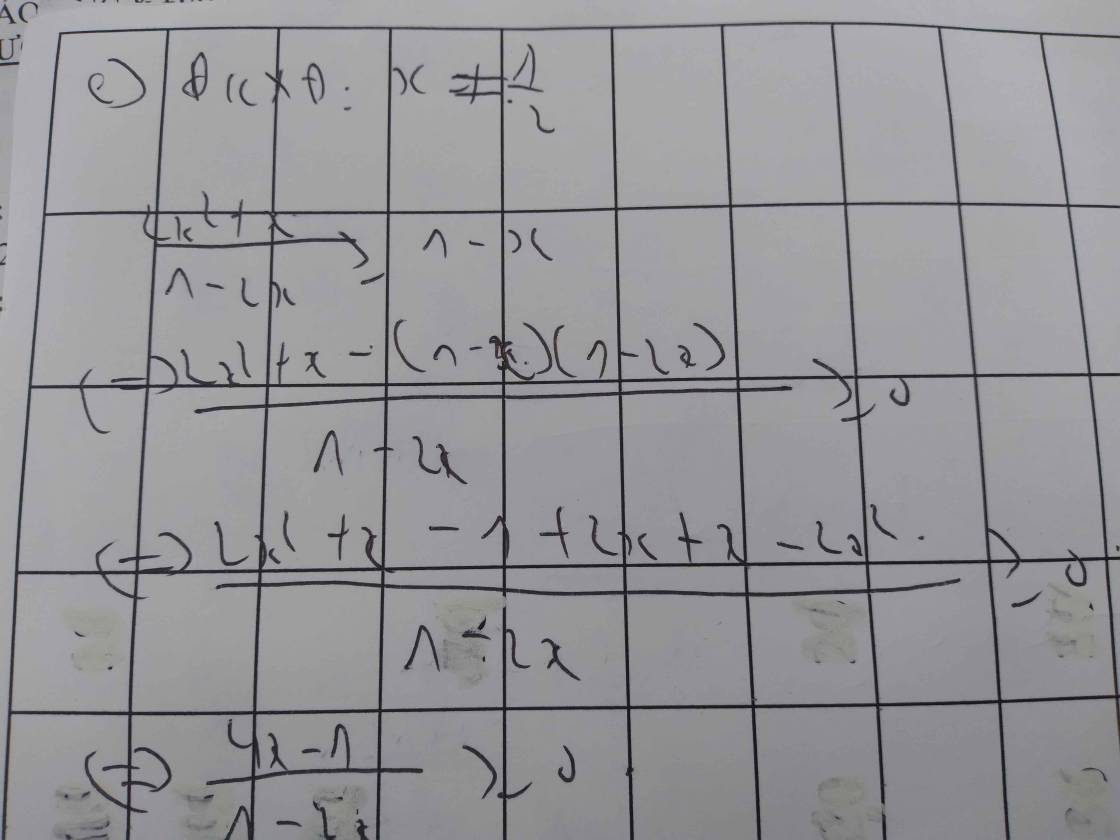
\(a,\Leftrightarrow\dfrac{\left(3x+4\right)\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}-\dfrac{x-2}{\left(x+2\right)\left(x-2\right)}=\dfrac{4+3x^2-12}{\left(x-2\right)\left(x+2\right)}\)
ĐKXĐ:\(x\ne2;x\ne-2\)
\(\Rightarrow3x^2+10x+8-x+2-4-3x^2+12=0\)
\(\Leftrightarrow\)\(9x+18=0\)
\(\Leftrightarrow x=-2\)(loại).
Vậy phương trình vô nghiệm.
b,ĐKXĐ:\(x\ne\dfrac{1}{2}\)
PT đã cho \(\Rightarrow6x^2-4x+6-6x^2+13x-5=0\)
\(\Leftrightarrow9x+1=0\)
\(\Leftrightarrow x=-\dfrac{1}{9}\left(tmđk\right)\)
c,\(ĐKXĐ:x\ge2\)
Bình phương 2 vế ta được:
\(x^2-4-x^2+2x-1=0\)
\(\Leftrightarrow2x-5=0\)
\(\Leftrightarrow x=\dfrac{5}{2}\left(tmđk\right)\)




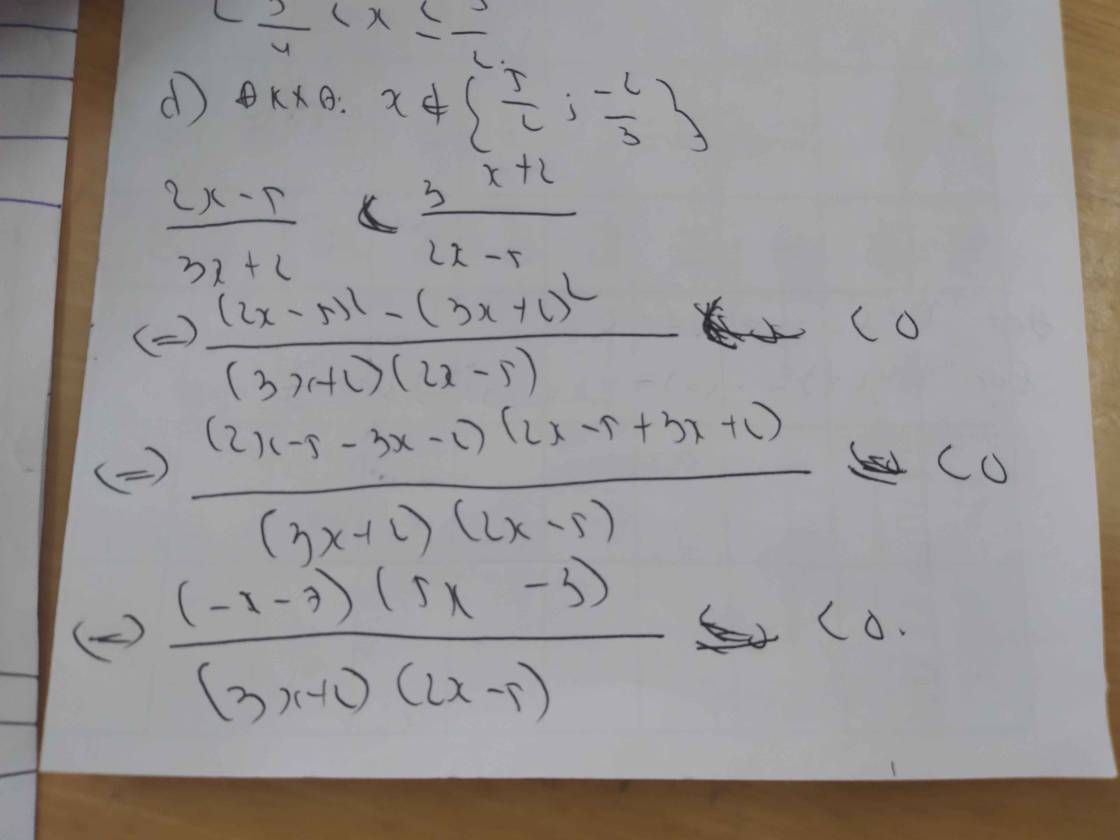


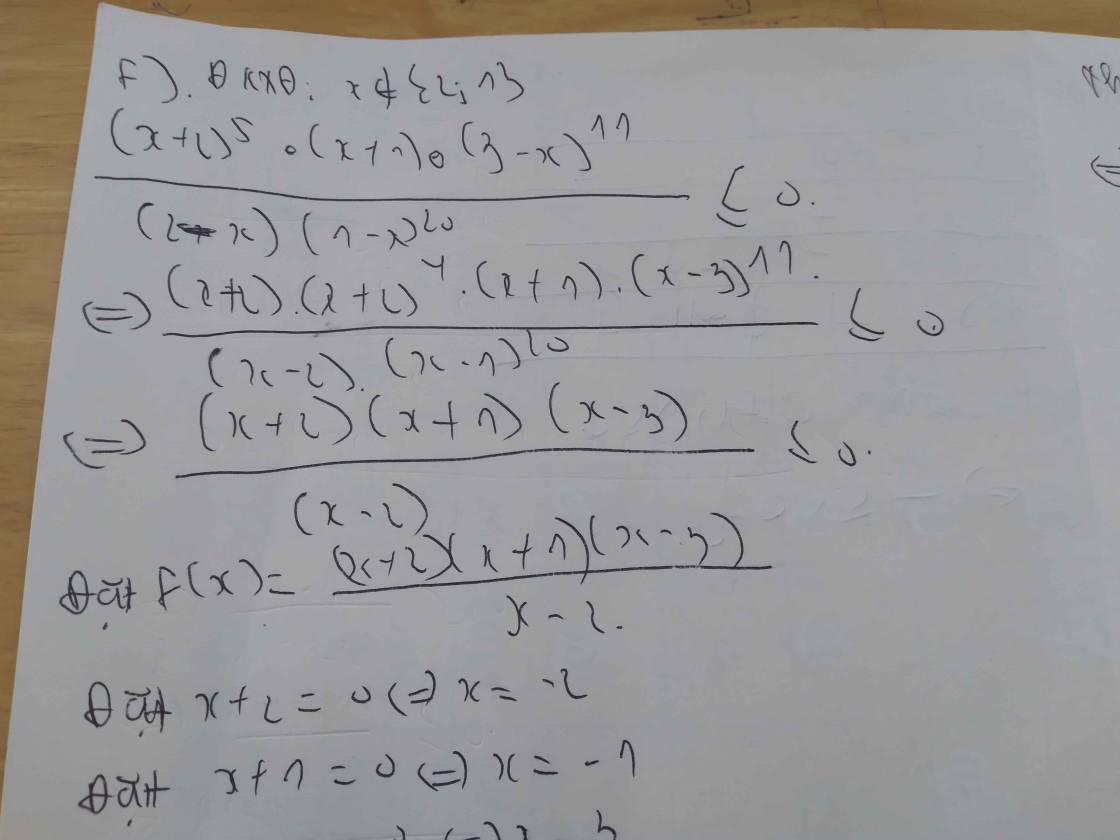



Đặt \(\left\{{}\begin{matrix}x-2008=n\\2x+2009=h\\3x-2011=t\end{matrix}\right.\Rightarrow n+h+t=6x-2010\)
\(\Rightarrow pt\Leftrightarrow\dfrac{1}{n}+\dfrac{1}{h}=\dfrac{1}{n+h+t}-\dfrac{1}{t}\)
\(\Leftrightarrow\dfrac{n+h}{hn}=\dfrac{-\left(n+h\right)}{t\left(n+h+t\right)}\)
\(\Leftrightarrow\left(n+h\right)\left(\dfrac{1}{hn}+\dfrac{1}{t\left(n+h+t\right)}\right)=0\)
\(\Leftrightarrow\left(n+h\right)\dfrac{t\left(n+h+t\right)+hn}{hnt\left(n+h+t\right)}=0\)
\(\Leftrightarrow\dfrac{\left(n+h\right)\left(n+t\right)\left(t+h\right)}{hnt\left(n+h+t\right)}=0\)
\(\Rightarrow\left[{}\begin{matrix}n=-h\\n=-t\\t=-h\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x-2008=-\left(2x+2009\right)\\x-2008=-\left(3x-2011\right)\\3x-2011=-\left(2x+2009\right)\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{1}{3}\\x=\dfrac{4019}{4}\\x=\dfrac{2}{5}\end{matrix}\right.\)