
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a,
c, Gọi \(\left(D_3\right):y=ax+b\) là đt cần tìm
\(\Leftrightarrow\left\{{}\begin{matrix}a=-2;b\ne0\\3x+3=ax+b,\forall x=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2\\-a+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b=-2\end{matrix}\right.\)
Vậy \(\left(D_3\right):y=-2x-2\)



\(\sqrt{12+2\sqrt{18}}.\dfrac{6-\sqrt{3}}{3+\sqrt{3}}\)
\(\sqrt{24+4\sqrt{18}}.\dfrac{6-\sqrt{3}}{3\sqrt{2}+\sqrt{6}}\)
\(\left(\sqrt{18}+2\right).\dfrac{\sqrt{3}\left(2\sqrt{3}-1\right)}{\sqrt{6}\left(\sqrt{3}+1\right)}\)

\(C=\sqrt{\left(\sqrt{x}-1\right)^2}+\sqrt{\left(\sqrt{x}+1\right)^2}=\sqrt{x}-1+\sqrt{x}+1=2\sqrt{x}\\ D=\sqrt{\left(\sqrt{x-1}+1\right)^2}+\sqrt{\left(\sqrt{x-1}-1\right)^2}\\ D=\sqrt{x-1}+1+\sqrt{x-1}-1=2\sqrt{x-1}\)

Công thức đây nhé (Áp dụng làm thử đi)
Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc , kí hiệu .Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc , kí hiệu .
Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc , kí hiệu .
Tỉ số giữa cạnh kề và cạnh đối gọi là côtang của góc , kí hiệu .

\(a,A=\left(\dfrac{x+14\sqrt{x}-5}{x-25}+\dfrac{\sqrt{x}}{\sqrt{x}+5}\right):\dfrac{\sqrt{x}+2}{\sqrt{x}-5}\)
\(\Rightarrow A=\left(\dfrac{x+14\sqrt{x}-5}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}+\dfrac{\sqrt{x}\left(\sqrt{x}-5\right)}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}\right).\dfrac{\sqrt{x}-5}{\sqrt{x}+2}\)
\(\Rightarrow A=\left(\dfrac{x+14\sqrt{x}-5}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}+\dfrac{x-5\sqrt{x}}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}\right).\dfrac{\sqrt{x}-5}{\sqrt{x}+2}\)
\(\Rightarrow A=\dfrac{x+14\sqrt{x}-5+x-5\sqrt{x}}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}.\dfrac{\sqrt{x}-5}{\sqrt{x}+2}\)
\(\Rightarrow A=\dfrac{2x+9\sqrt{x}-5}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}.\dfrac{\sqrt{x}-5}{\sqrt{x}+2}\)
\(\Rightarrow A=\dfrac{2x+10\sqrt{x}-\sqrt{x}-5}{\left(\sqrt{x}+5\right)\left(\sqrt{x}+2\right)}\)
\(\Rightarrow A=\dfrac{2\sqrt{x}\left(\sqrt{x}+5\right)-\left(\sqrt{x}+5\right)}{\left(\sqrt{x}+5\right)\left(\sqrt{x}+2\right)}\)
\(\Rightarrow A=\dfrac{\left(2\sqrt{x}-1\right)\left(\sqrt{x}+5\right)}{\left(\sqrt{x}+5\right)\left(\sqrt{x}+2\right)}\)
\(\Rightarrow A=\dfrac{2\sqrt{x}-1}{\sqrt{x}+2}\)

Câu 6: Để hàm số y=(1-m)x+3 nghịch biến trên R thì 1-m<0
=>m>1
=>Chọn B
Câu 7: D
Câu 10: (D)//(D')
=>\(\left\{{}\begin{matrix}3m+1=2\left(m+1\right)\\-2\ne-2\left(loại\right)\end{matrix}\right.\Leftrightarrow m\in\varnothing\)
=>Chọn D
Câu 11: \(x^2+2x+2=\left(x+1\right)^2+1>=1>0\forall x\)
=>\(\sqrt{x^2+2x+2}\) luôn xác định với mọi số thực x
=>Chọn A
Câu 12: Để hai đường thẳng y=x+3m+2 và y=3x+2m+3 cắt nhau tại một điểm trên trục tung thì \(\left\{{}\begin{matrix}1\ne3\left(đúng\right)\\3m+2=2m+3\end{matrix}\right.\)
=>3m+2=2m+3
=>m=1
=>Chọn C

\(b,\text{PT hoành độ giao điểm: }-2x=3x+3\\ \Leftrightarrow x=-\dfrac{3}{5}\Leftrightarrow y=\dfrac{6}{5}\\ \Leftrightarrow A\left(-\dfrac{3}{5};\dfrac{6}{5}\right)\)



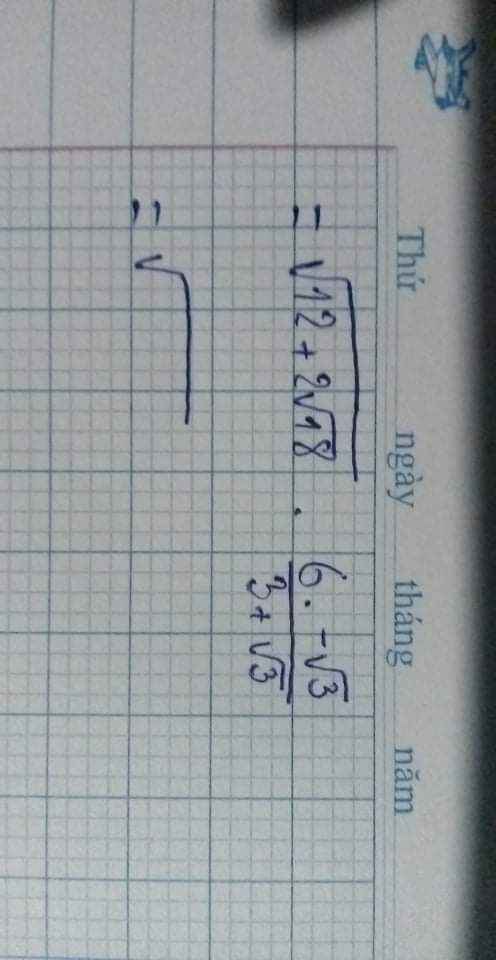





a: Xét ΔCNM vuông tại N và ΔCAB vuông tại A có
\(\widehat{C}\) chung
Do đó: ΔCNM\(\sim\)ΔCAB
Suy ra: \(\dfrac{CN}{CA}=\dfrac{CM}{CB}\)
hay \(\dfrac{AC}{BC}=\dfrac{NC}{MC}\)