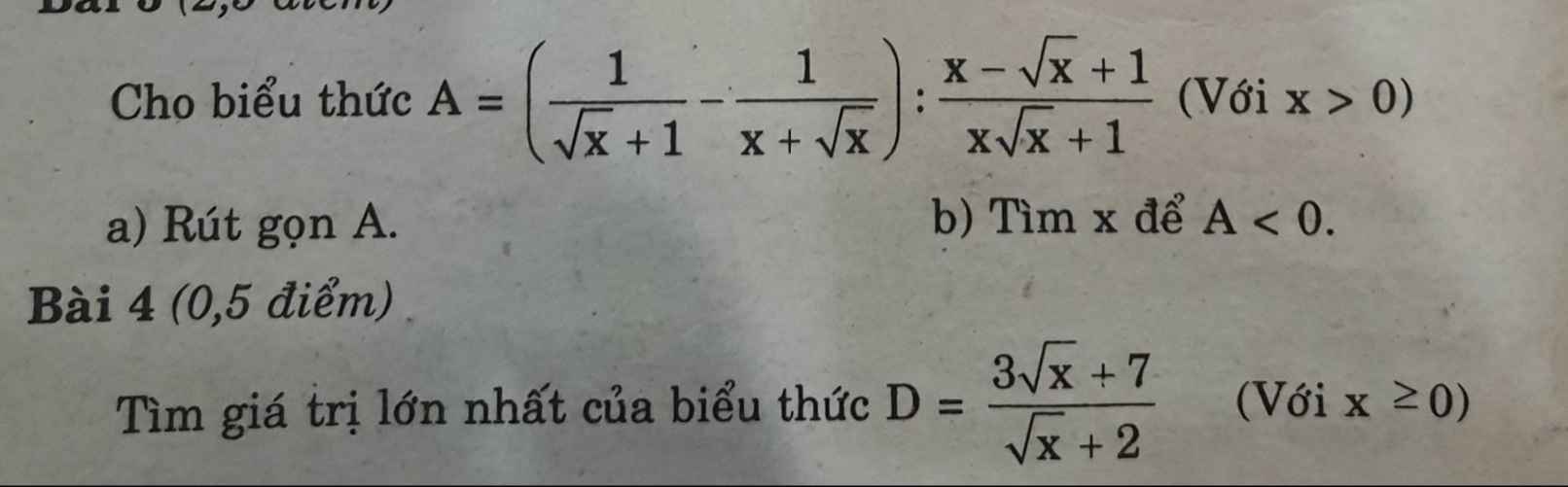K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
4 tháng 9 2021
Bài 2:
a: Vì (d) có hệ số góc là 3 nên a=3
Vậy: (d): y=3x+b
Thay x=1 và y=0 vào (d), ta được:
b+3=0
hay b=-3
b: Vì (d)//y=0,5x-2 nên a=0,5
Vậy: (d): y=0,5x+b
Thay x=0 và y=2 vào (d), ta được:
b=2
GIẢI HỘ EM BÀI 3 VỚI Ạ
NA
0
22 tháng 1
1: ĐKXĐ: x<>1 và y>=2
\(\left\{{}\begin{matrix}\dfrac{2}{x-1}-\sqrt{y-2}=-1\\\dfrac{3}{x-1}+2\sqrt{y-2}=9\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{4}{x-1}-2\sqrt{y-2}=-2\\\dfrac{3}{x-1}+2\sqrt{y-2}=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{7}{x-1}=7\\\dfrac{3}{x-1}+2\sqrt{y-2}=9\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x-1=1\\2\sqrt{y-2}=9-3=6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x-1=1\\\sqrt{y-2}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y-2=9\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=2\\y=11\end{matrix}\right.\left(nhận\right)\)
2:
a: Phương trình hoành độ giao điểm là:
\(x^2-\left(m-2\right)x-m-4=0\)
\(\text{Δ}=\left[-\left(m-2\right)\right]^2-4\left(-m-4\right)\)
\(=m^2-4m+4+4m+16\)
\(=m^2+20>=20>0\forall m\)
=>(d) luôn cắt (P) tại hai điểm phân biệt
b: Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=\dfrac{-\left[-\left(m-2\right)\right]}{1}=m-2\\x_1\cdot x_2=\dfrac{c}{a}=-m-4\end{matrix}\right.\)
\(\left|x_1+x_2\right|=\left|x_1-x_2\right|\)
=>\(\left[{}\begin{matrix}x_1+x_2=x_1-x_2\\x_1+x_2=-x_1+x_2\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}-2x_2=0\\2x_1=0\end{matrix}\right.\Leftrightarrow x_1\cdot x_2=0\)
=>-m-4=0
=>m+4=0
=>m=-4
4 tháng 11 2021
b, PTGD (d1) và trục hoành là \(2x+5=0\Leftrightarrow x=-\dfrac{5}{2}\Leftrightarrow B\left(-\dfrac{5}{2};0\right)\Leftrightarrow OB=\dfrac{5}{2}\)
PTGD (d2) và trục hoành là \(2-x=0\Leftrightarrow x=2\Leftrightarrow A\left(2;0\right)\Leftrightarrow OA=2\)
Do đó \(AB=OA+OB=\dfrac{9}{2}\)
PTHDGD (d1) và (d2) là \(2x+5=2-x\Leftrightarrow x=-1\Leftrightarrow y=3\Leftrightarrow C\left(-1;3\right)\)
Gọi H là chân đg cao từ C tới Ox thì \(CH=3\)
Do đó \(S_{ABC}=\dfrac{1}{2}CH\cdot AB=\dfrac{1}{2}\cdot\dfrac{9}{2}\cdot3=\dfrac{27}{4}\left(đvdt\right)\)
c, Vì \(-1=-1;2\ne4\) nên (d2)//(d3)
NT
1
22 tháng 8 2021
a: Ta có: \(A=\left(\dfrac{1}{\sqrt{x}+1}-\dfrac{1}{x+\sqrt{x}}\right):\dfrac{x-\sqrt{x}+1}{x\sqrt{x}+1}\)
\(=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}+1}{1}\)
\(=\dfrac{x-1}{\sqrt{x}}\)
b: Để A<0 thì x-1<0
hay x<1
Kết hợp ĐKXĐ, ta được: 0<x<1
22 tháng 8 2021
với \(x\ge0\) ta có :\(D=\dfrac{3\sqrt{x+7}}{\sqrt{x}+2}=\dfrac{3\left(\sqrt{x}+2\right)+1}{\sqrt{x}+2}=3+\dfrac{1}{\sqrt{x}+2}\)
D lớn nhất \(\Leftrightarrow\sqrt{x}+2\) nhỏ nhất:
Mà:\(\sqrt{x}+2\ge2\)
vậy:\(\max\limits_D=3+\dfrac{1}{2}=\dfrac{7}{2}\Leftrightarrow x=0\)