K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
10 tháng 1 2022
Bài 4:
\(\Leftrightarrow3x-6-1⋮x-2\)
\(\Leftrightarrow x-2\in\left\{1;-1\right\}\)
hay \(x\in\left\{3;1\right\}\)
31 tháng 7 2023
4:
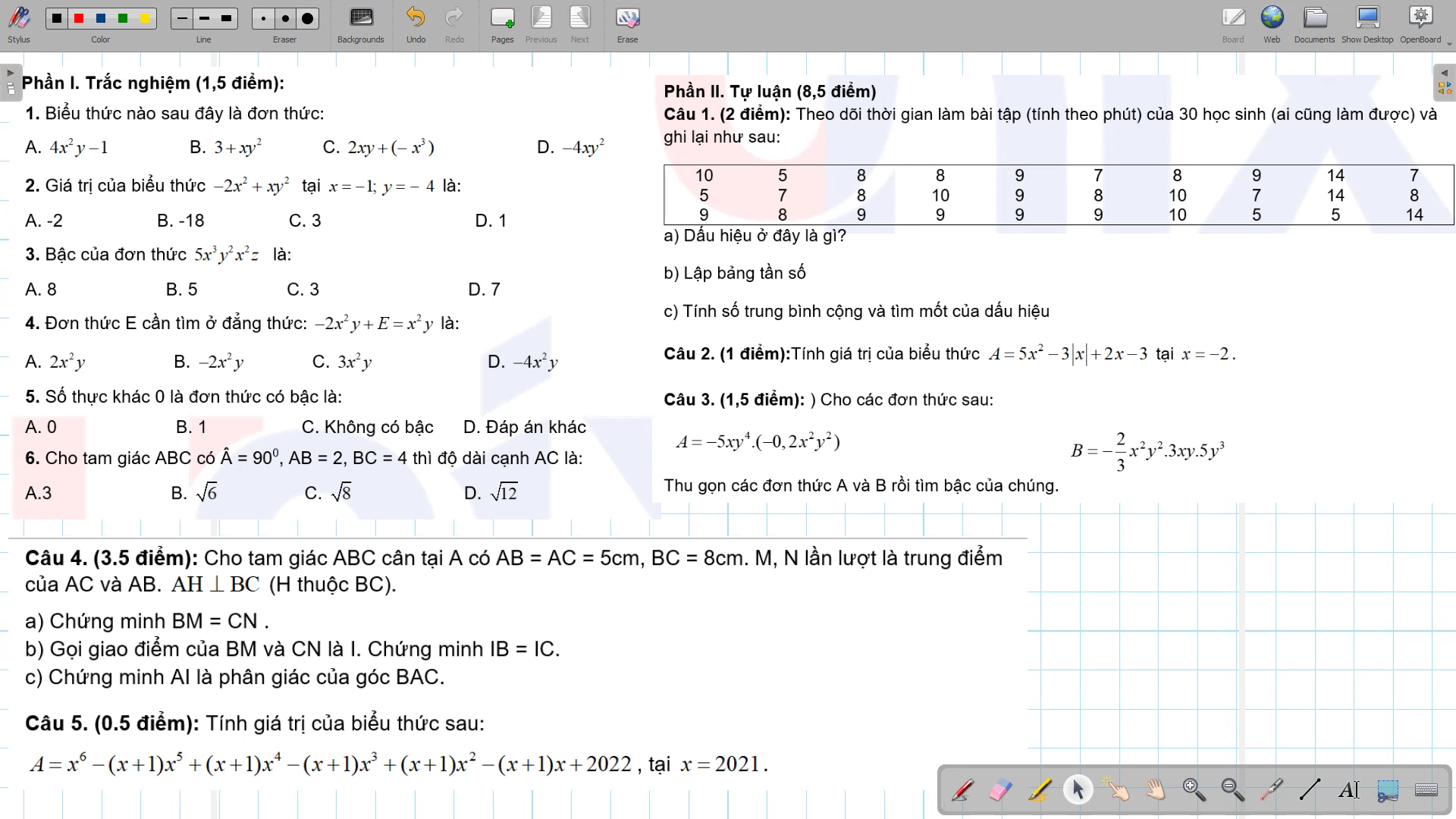
a: Xét ΔABM và ΔACN có
AB=AC
góc A chung
AM=AN
=>ΔABM=ΔACN
=>BM=CN
b: Xét ΔNBC và ΔMCB có
NB=MC
góc NBC=góc MCB
BC chung
=>ΔNBC=ΔMCB
=>góc IBC=góc ICB
=>IB=IC
c: Xét ΔABI và ΔACI có
AB=AC
IB=IC
AI chung
=>ΔABI=ΔACI
=>góc BAI=góc CAI
=>AI là phân giác của góc BAC
5 tháng 3 2022
Câu 3:
a: \(BD=\sqrt{BC^2-DC^2}=4\left(cm\right)\)
b: \(\widehat{A}=180^0-2\cdot70^0=40^0< \widehat{B}\)
nên BC<AC=AB
c: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó:ΔEBC=ΔDCB
d: Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)
nên ΔOBC cân tại O
KV
31 tháng 10 2023
Câu 2
a) Thay y = -2 vào biểu thức đã cho ta được:
2.(-2) + 3 = -1
Vậy giá trị của biểu thức đã cho tại y = -2 là -1
b) Thay x = -5 vào biểu thức đã cho ta được:
2.[(-5)² - 5] = 2.(25 - 5) = 2.20 = 40
Vậy giá trị của biểu thức đã cho tại x = -5 là 40
VT
3 tháng 1 2022
2xy - 3x + 5y=4
2x(y-1) + 5y = 4
2x(y-1) + 5y - 5 = 4 - 5
2x(y-1) - 1(y-1) = -1
(2x-1)(y-1) = -1
Ta thấy -1= (-1).1 => Ta có bảng sau:
| 2x-1 | -1 | 1 |
| y-1 | 1 | -1 |
| x | 0 | 1 |
| y | 2 | 0 |
Như vậy, ta có 2 trường hợp (x;y) thỏa mãn yêu cầu đề bài là ( 0;2 ) ; ( 1;0 )
Hok tốt~
4 tháng 1 2022
b: \(=\dfrac{3}{8}\left(19+\dfrac{1}{3}-33-\dfrac{1}{3}\right)=\dfrac{3}{8}\cdot\left(-14\right)=\dfrac{-42}{8}=\dfrac{-21}{4}\)
c: \(=\dfrac{27}{23}+\dfrac{5}{21}-\dfrac{4}{23}+\dfrac{1}{2}+\dfrac{16}{21}=2+\dfrac{1}{2}=\dfrac{5}{2}\)
d: \(=\dfrac{21+26}{47}+\dfrac{1+4}{5}=2\)
HD
0
20 tháng 9 2021
\(D=10\cdot\left(-2.5\right)\cdot0.4\cdot\left(-0.1\right)\)
\(=10\cdot1\cdot2.5\cdot0.4\)
=10
\(\text{#TNam}\)
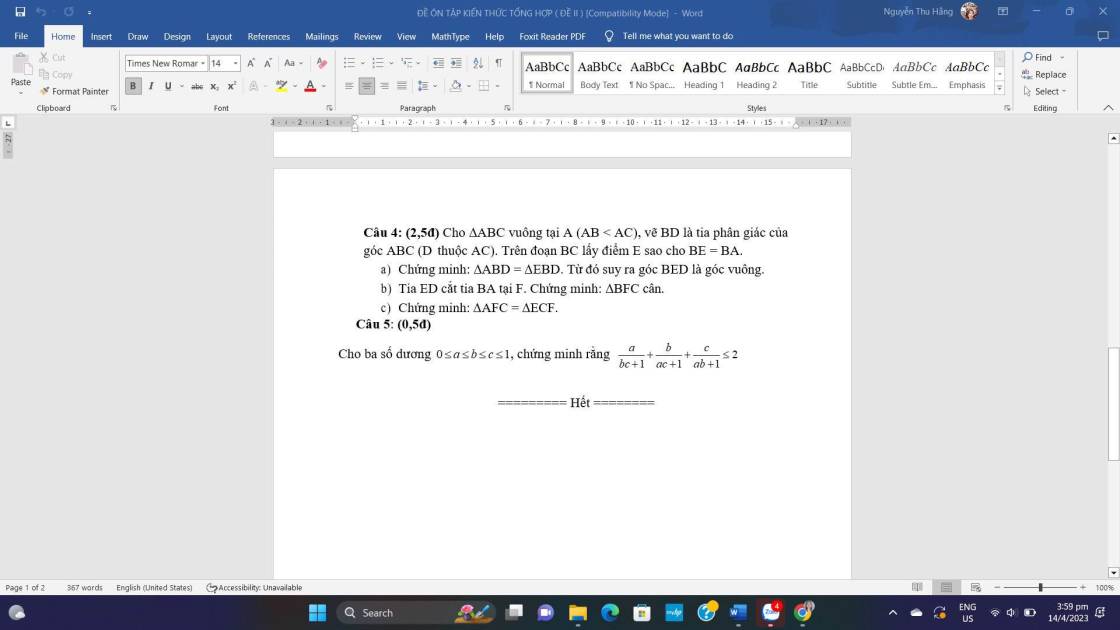
`a,`
Xét Tam giác `ABD` và Tam giác `EBD` có:
`AB = EB (g``t)`
\(\widehat{ABD}=\widehat{EBD} (\text {tia phân giác}\) \(\widehat{ABE})\)
`\text {BD chung}`
`=> \text {Tam giác ABD = Tam giác EBD (c-g-c)}`
`->`\(\widehat{BAD}=\widehat{BED} (\text {2 góc tương ứng})\)
Mà \(\widehat{BAD}=90^0\)
`->`\(\widehat{BAD}=\widehat{BED}=90^0\)
`->`\(\widehat{BED}\) \(\text {là góc vuông}\)
`b,`
Xét Tam giác `BAC` và Tam giác `BEF` có:
\(\widehat{BAC}=\widehat{BEF}=90^0\)
`BA = BE (g``t)`
\(\widehat{B}\) \(\text {chung}\)
`=> \text {Tam giác BAC = Tam giác BEF (g-c-g)}`
`-> BF = BC (\text {2 cạnh tương ứng})`
Xét Tam giác `BFC:`
`BF = BC (CMT)`
`-> text {Tam giác BFC cân tại B}`
`c,`
Vì Tam giác `BFC` cân tại `B`
`->`\(\widehat{F}=\widehat{C}\)
Xét Tam giác `AFC` và Tam giác `ECF` có:
\(\widehat{F}=\widehat{C}\)
`\text {FC chung}`
\(\widehat{CAF}=\widehat{FEC}=90^0\)
`=> \text {Tam giác AFC = Tam giác ECF (ch-gn)}`