
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



b, ( \(\dfrac{1}{6}\))2.62 + \(\dfrac{\left(0,6\right)^5}{\left(0,2\right)^6}\)
= (\(\dfrac{6}{6}\))2 + ( \(\dfrac{0,6}{0,2}\))5. \(\dfrac{1}{0,2}\)
= 1 + 35. \(\dfrac{1}{0,2}\)
= 1 + 1215
= 1216


\(\text{#TNam}\)
`a,`
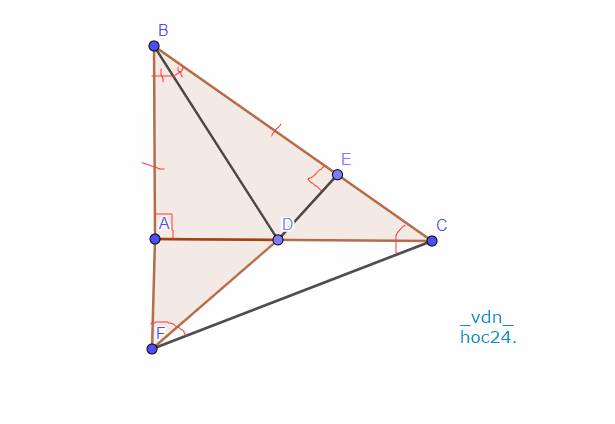
Xét Tam giác `ABD` và Tam giác `EBD` có:
`AB = EB (g``t)`
\(\widehat{ABD}=\widehat{EBD} (\text {tia phân giác}\) \(\widehat{ABE})\)
`\text {BD chung}`
`=> \text {Tam giác ABD = Tam giác EBD (c-g-c)}`
`->`\(\widehat{BAD}=\widehat{BED} (\text {2 góc tương ứng})\)
Mà \(\widehat{BAD}=90^0\)
`->`\(\widehat{BAD}=\widehat{BED}=90^0\)
`->`\(\widehat{BED}\) \(\text {là góc vuông}\)
`b,`
Xét Tam giác `BAC` và Tam giác `BEF` có:
\(\widehat{BAC}=\widehat{BEF}=90^0\)
`BA = BE (g``t)`
\(\widehat{B}\) \(\text {chung}\)
`=> \text {Tam giác BAC = Tam giác BEF (g-c-g)}`
`-> BF = BC (\text {2 cạnh tương ứng})`
Xét Tam giác `BFC:`
`BF = BC (CMT)`
`-> text {Tam giác BFC cân tại B}`
`c,`
Vì Tam giác `BFC` cân tại `B`
`->`\(\widehat{F}=\widehat{C}\)
Xét Tam giác `AFC` và Tam giác `ECF` có:
\(\widehat{F}=\widehat{C}\)
`\text {FC chung}`
\(\widehat{CAF}=\widehat{FEC}=90^0\)
`=> \text {Tam giác AFC = Tam giác ECF (ch-gn)}`

7:
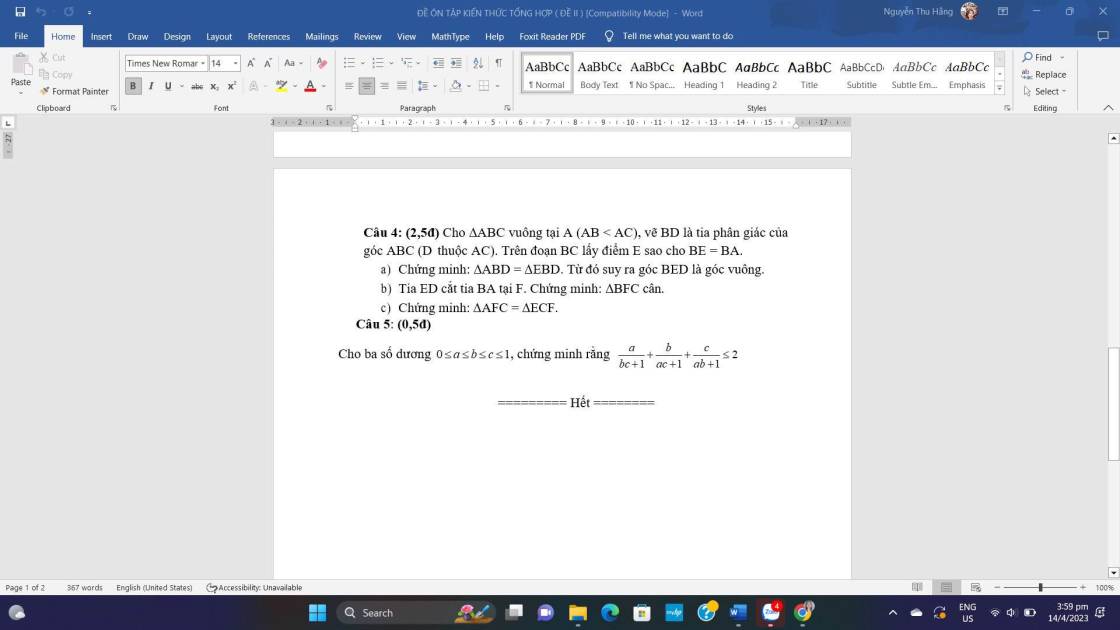
A+B
\(=x^4-2xy+y^2+y^2+2xy+x^2+1\)
=x^4+2y^2+x^2+1
A-B
=x^4-2xy+y^2-y^2-2xy-x^2-1
=x^4-4xy-x^2-1
5:
a: =8x^2-4x^2=4x^2
b: =(5-7)*x^2y^3z^3=-2x^2y^3z^3
c: =(3+2-1/3-1/2-1/6)*x^2y^2
=4x^2y^2


4:
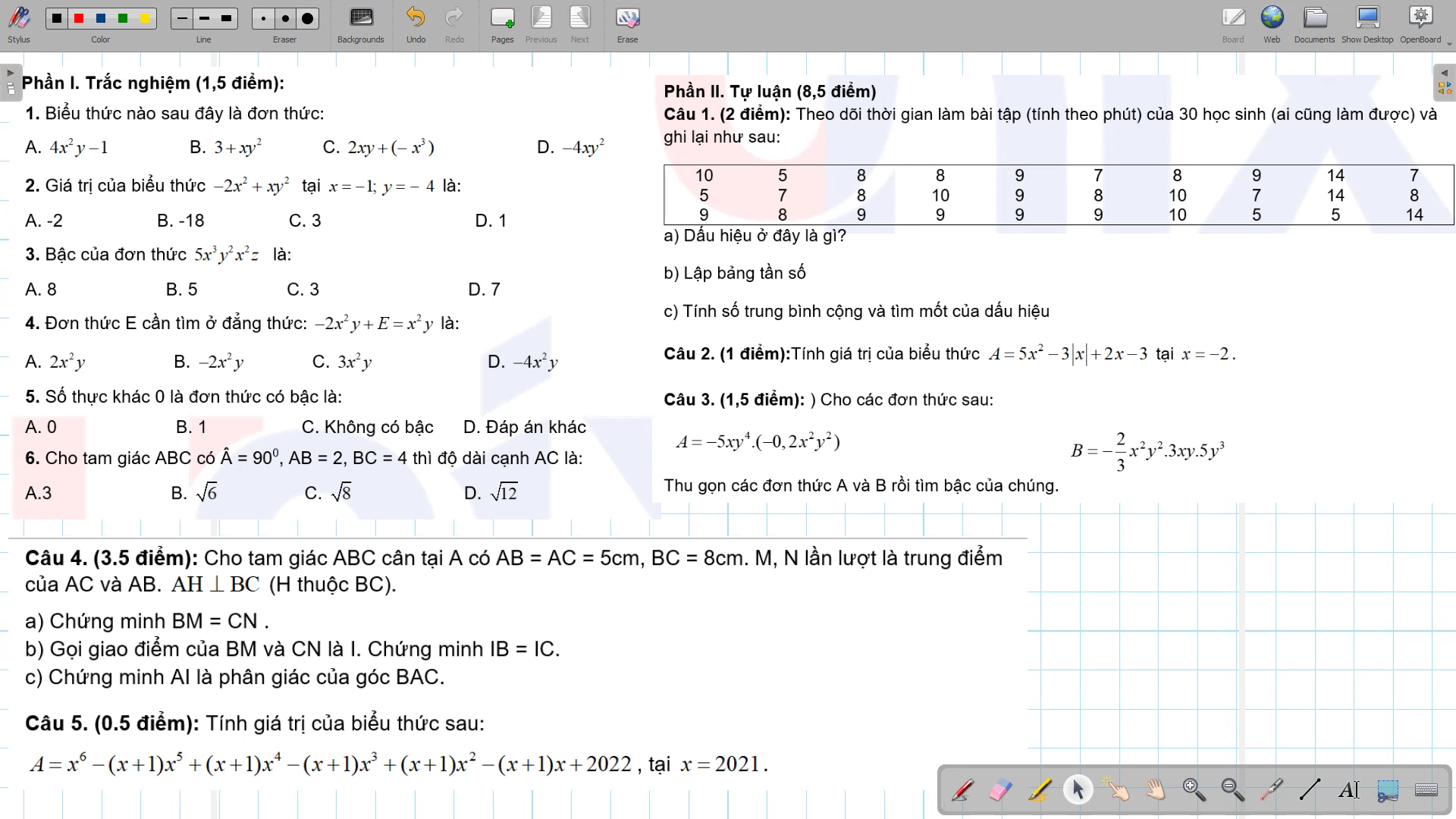
a: Xét ΔABM và ΔACN có
AB=AC
góc A chung
AM=AN
=>ΔABM=ΔACN
=>BM=CN
b: Xét ΔNBC và ΔMCB có
NB=MC
góc NBC=góc MCB
BC chung
=>ΔNBC=ΔMCB
=>góc IBC=góc ICB
=>IB=IC
c: Xét ΔABI và ΔACI có
AB=AC
IB=IC
AI chung
=>ΔABI=ΔACI
=>góc BAI=góc CAI
=>AI là phân giác của góc BAC




Bài 4:
\(\Leftrightarrow3x-6-1⋮x-2\)
\(\Leftrightarrow x-2\in\left\{1;-1\right\}\)
hay \(x\in\left\{3;1\right\}\)