
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
3: ĐKXĐ: x>=1
\(x-\sqrt{x+3+4\sqrt{x-1}}=1\)
=>\(x-\sqrt{x-1+2\cdot\sqrt{x-1}\cdot2+4}=1\)
=>\(x-\sqrt{\left(\sqrt{x-1}+2\right)^2}=1\)
=>\(x-\left|\sqrt{x-1}+2\right|=1\)
=>\(x-\left(\sqrt{x-1}+2\right)=1\)
=>\(x-\sqrt{x-1}-2-1=0\)
=>\(x-1-\sqrt{x-1}-2=0\)
=>\(\left(\sqrt{x-1}\right)^2-2\sqrt{x-1}+\sqrt{x-1}-2=0\)
=>\(\left(\sqrt{x-1}-2\right)\left(\sqrt{x-1}+1\right)=0\)
=>\(\sqrt{x-1}-2=0\)
=>\(\sqrt{x-1}=2\)
=>x-1=4
=>x=5(nhận)

Câu 2:
Ta có: \(\sqrt{x^2-4x+4}=x-1\)
\(\Leftrightarrow2-x=x-1\left(x< 2\right)\)
\(\Leftrightarrow-2x=-3\)
hay \(x=\dfrac{3}{2}\left(tm\right)\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2x-3=2\cdot1-3=-1\end{matrix}\right.\)

16:
a: ĐKXĐ: x>0
\(x+\dfrac{1}{x}+\sqrt{x}+\dfrac{1}{\sqrt{x}}=4\)
\(x+\dfrac{1}{x}>=2\cdot\sqrt{x\cdot\dfrac{1}{x}}=2\)
\(\sqrt{x}+\dfrac{1}{\sqrt{x}}>=2\cdot\sqrt{\sqrt{x}\cdot\dfrac{1}{\sqrt{x}}}=2\)
Do đó: \(x+\dfrac{1}{x}+\sqrt{x}+\dfrac{1}{\sqrt{x}}>=2+2=4\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x^2=1\\x=1\end{matrix}\right.\)
=>x=1

Điều kiện:`a>=0,a ne 1` $\\$ `E=(1+(a-sqrta)/(sqrta-1))(1-(a+sqrta)/(1+sqrta))`
`=(1+(sqrta(sqrta-1))/(sqrta-1))(1-(sqrta(sqrta+1))/(sqrta+1))`
`=(1+sqrta)(1-sqrta)`
`=1-a`
\(E=\left(1+\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\right)\left(1-\dfrac{a+\sqrt{a}}{1+\sqrt{a}}\right)\)
ĐK: a ≥ 0; a khác 1
\(=\left[1+\dfrac{\sqrt{a}\left(\sqrt{a}-1\right)}{\sqrt{a}-1}\right]\left[1-\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)}{\sqrt{a}+1}\right]\)
\(=\left(1+\sqrt{a}\right)\left(1-\sqrt{a}\right)=1-a\)

Bài 2:
a: \(\dfrac{2-\sqrt{3}}{3\sqrt{6}}=\dfrac{2\sqrt{6}-3\sqrt{2}}{18}\)
b: \(\dfrac{1}{\sqrt{3}+\sqrt{2}}=\sqrt{3}-\sqrt{2}\)







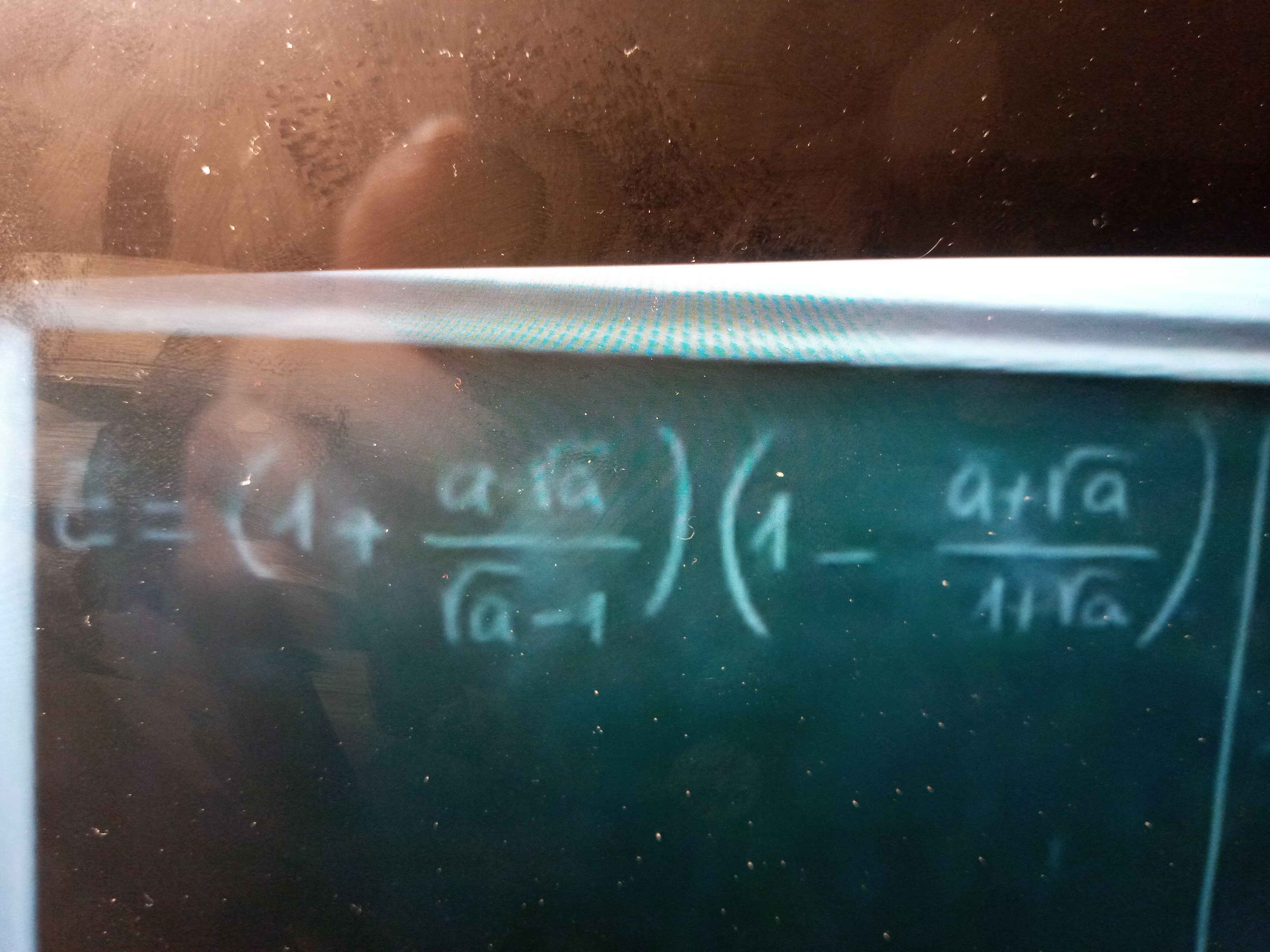

a: Xét ΔAHB vuông tại H có HE là đường cao ứng với cạnh huyền AB, ta được:
\(AE\cdot AB=AH^2\left(1\right)\)
Xét ΔHAC vuông tại H có HF là đường cao ứng với cạnh huyền AC, ta được:
\(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
hay \(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Xét ΔAEF vuông tại A và ΔACB vuông tại A có
\(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Do đó: ΔAEF\(\sim\)ΔACB
Suy ra: \(\widehat{AEF}=\widehat{ACB}\)