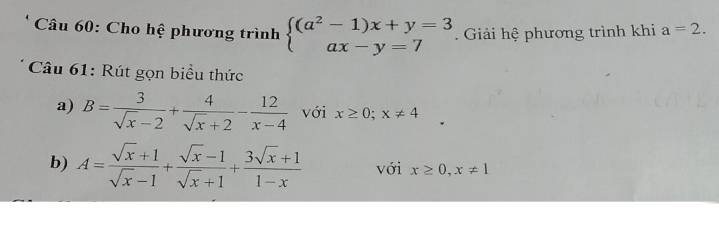K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
30 tháng 6 2023
1:
d: P=A+B
\(=\dfrac{2\sqrt{x}}{\sqrt{x}+3}+\dfrac{15-\sqrt{x}+2\sqrt{x}-10}{x-25}\cdot\dfrac{\sqrt{x}-5}{\sqrt{x}+3}\)
\(=\dfrac{2\sqrt{x}}{\sqrt{x}+3}+\dfrac{1}{\sqrt{x}+3}=\dfrac{2\sqrt{x}+1}{\sqrt{x}+3}\)
P nguyên
=>2căn x+6-5 chia hết cho căn x+3
=>căn x+3 thuộc Ư(-5)
=>căn x+3=5
=>x=4
3:
2:
b: PTHĐGĐ là:
x^2-2(m+1)x+2m+1=0
Theo đề, ta có:
x1^2+x2^2=(căn 5)^2=5
=>(x1+x2)^2-2x1x2=5
=>(2m+2)^2-2(2m+1)=5
=>4m^2+8m+4-4m-2-5=0
=>4m^2+4m+1=0
=>m=-1/2
2
22 tháng 5 2022
`a)A` có nghĩa `<=>x-1 >= 0 <=>x >= 1`
`b)B=\sqrt{3^2 .2}+\sqrt{2^3}-\sqrt{5^2 .2}`
`<=>B=3\sqrt{2}+2\sqrt{2}-5\sqrt{2}`
`<=>B=0`
`c)` Với `a >= 0,a \ne 1` có:
`C=[a-1]/[\sqrt{a}-1]-[a\sqrt{a}-1]/[a-1]`
`C=[(a-1)(\sqrt{a}+1)-a\sqrt{a}+1]/[(\sqrt{a}-1)(\sqrt{a}+1)]`
`C=[a\sqrt{a}+a-\sqrt{a}-1-a\sqrt{a}+1]/[(\sqrt{a}-1)(\sqrt{a}+1)]`
`C=a/[a-1]`
S
27 tháng 11 2021
để em viết ra vậy ạ
cho tam giac mnp vuông tại m (mn>mp) có đường cao mk
a) biết mn=20cm, mp=15cm, tính mk và góc mnp (góc làm tròn đến đơn vị phút).
b) vẽ trung tuyến me của tam giác mnp. từ p vẽ đường thẳng vuông góc với me cắt mn tại d. cm tam giác mnp đồng dạng với tam giác mpd, từ đó suy ra mn.md=np.pk
1N
1
22 tháng 12 2023
Câu 61:
a: \(B=\dfrac{3}{\sqrt{x}-2}+\dfrac{4}{\sqrt{x}+2}-\dfrac{12}{x-4}\)
\(=\dfrac{3}{\sqrt{x}-2}+\dfrac{4}{\sqrt{x}+2}-\dfrac{12}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{3\left(\sqrt{x}+2\right)+4\left(\sqrt{x}-2\right)-12}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{3\sqrt{x}+6+4\sqrt{x}-8-12}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{7\sqrt{x}-14}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{7\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{7}{\sqrt{x}+2}\)
b: \(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}+\dfrac{\sqrt{x}-1}{\sqrt{x}+1}+\dfrac{3\sqrt{x}+1}{1-x}\)
\(=\dfrac{\left(\sqrt{x}+1\right)}{\sqrt{x}-1}+\dfrac{\sqrt{x}-1}{\sqrt{x}+1}-\dfrac{3\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\left(\sqrt{x}+1\right)^2+\left(\sqrt{x}-1\right)^2-3\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x+2\sqrt{x}+1+x-2\sqrt{x}+1-3\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{2x-3\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\left(\sqrt{x}-1\right)\left(2\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}\)
Câu 60
Khi a=2 thì hệ phương trình sẽ trở thành:
\(\left\{{}\begin{matrix}\left(2^2-1\right)x+y=3\\2x-y=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x+y=3\\2x-y=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x=10\\2x-y=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=2\\y=2x-7=2\cdot2-7=-3\end{matrix}\right.\)
9 tháng 5 2022
a> Vì tam giác ABC vuông tại A => góc BAC = 90 hay BAD = 90
Vì DE \(\perp\) BC => BED =90
Xét tứ giác ABED có :
BAD +BED = 180
mà góc ở vị trí đối diện
=> Tứ giác ABED nội tiếp
=> Tâm của đường tròn nội tiếp tứ giác ABED là trung điểm của cạnh BD
b> Vì góc BAC = 90 => ABC + ACB = 90 *
Vì AK \(\perp BC\) =>KAB + ABK =90 **
Từ * và ** => ABK = ACB
Mà góc ABK =góc BHK < tứ giác ABED nt>
=> góc ACB = góc BHK
c> Xét tam giác BKH và tam giác BDC có:
góc BHK = góc ACB cmt
góc DBC Chung
=> tam giác BKH đồng dạng vs tam giác BDC <g-g>
=> \(\dfrac{BK}{BD}=\dfrac{HK}{CD}\)
<=> \(\dfrac{BK}{HK}=\dfrac{BD}{CD}\)
=> BK.CD = HK . BD
TM
4 tháng 11 2023
a, xét \(\Delta ABC\left(\widehat{BAC}=90^o\right)\) có \(AM\) là đường cao
\(BC^2=AB^2+AC^2\left(pytago\right)\Leftrightarrow BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
\(sinABC=\dfrac{AC}{BC}=\dfrac{16}{20}\Rightarrow\widehat{ABC}\approx53^o8'\)
\(sinACB=\dfrac{AB}{BC}=\dfrac{12}{20}\Rightarrow\widehat{ACB}\approx32^o52'\)
\(AB^2=BM.BC\Rightarrow BM=\dfrac{AB^2}{BC}=\dfrac{12^2}{20}=7,2\left(cm\right)\)
b, Xét \(\Delta ABM\left(\widehat{AMB}=90^o\right)\) có \(AE\perp AB\)
\(AB^2=BM^2+AM^2\left(pytago\right)\Leftrightarrow AM=\sqrt{20^2-7,2^2}=\dfrac{16\sqrt{34}}{5}\left(cm\right)\)
\(AM^2=AE.AB\) (hệ thức lượng trong tam giác vuông)\(\left(1\right)\)
c, Xét \(\Delta AMC\left(\widehat{AMC}=90^o\right)\)
\(AC^2=AM^2+MC^2\left(pytago\right)\Leftrightarrow AM^2=AC^2-MC^2\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow AE.AB=AC^2-MC^2\left(đpcm\right)\)