
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\widehat{C}=30^0\)
AB=10cm
\(AC=10\sqrt{3}\left(cm\right)\)

a: Xét ΔSBM và ΔSNB có
\(\widehat{SBM}=\widehat{SNB}\)
\(\widehat{BSM}\) chung
Do đó: ΔSBM\(\sim\)ΔSNB
Suy ra: SB/SN=SM/SB
hay \(SB^2=SM\cdot SN\)
b: Xét (O) có
SA là tiếp tuyến
SB là tiếp tuyến
Do đó: SA=SB
mà OA=OB
nên SO là đường trung trực của AB
=>SO⊥AB
Xét ΔOBS vuông tại B có BH là đường cao
nên \(SH\cdot SO=SB^2=SM\cdot SN\)

a: Ta có: BC⊥BA tại B
nên BC là tiếp tuyến của (A;AB)
b: Xét (A) có
CB là tiếp tuyến
CD là tiếp tuyến
Do đó: CB=CD
hay C nằm trên đường trung trực của BD(1)
Ta có: AB=AD
nên A nằm trên đường trung trực của BD(2)
Từ (1) và (2) suy ra AC là đường trung trực của BD
hay AC\(\perp\)BD
Giúp mình luôn câu c d được không:((( sắp hết h rồi mà không bt làm

b: Gọi giao của AH với BC là F
=>AH vuông góc BC tại F
góic CHI=góc AHD=90 độ-góc HAD=góc ABC=1/2*sđ cung AC
góc CIH=1/2*sđ cung CA
=>góc CHI=góc CIH
=>ΔCHI cân tại C
c:
góc BDC=góc BEC=90 độ
=>BDEC nội tiếp đường tròn đường kính BC
=>MD=ME
=>ΔMDE cân tại M
mà MN là trung tuyến
nên MN vuông góc DE
Kẻ tiếp tuyến Ax của (O)
=>góc xAC=góc ABC
=>góc xAC=góc AED
=>Ax//DE
=>DE vuông góc OA
=>MN//AO


a: AC=12(cm)
\(\sin\widehat{C}=\dfrac{9}{15}=\dfrac{3}{5}\)
\(\Leftrightarrow C=37^0\)
\(\Leftrightarrow\widehat{B}=53^0\)

a: AI=8cm
=>AB=16cm
b: Xét ΔMAO và ΔMBO có
OA=OB
\(\widehat{MOA}=\widehat{MOB}\)
OM chung
Do đó: ΔMAO=ΔMBO
Suy ra: \(\widehat{MAO}=\widehat{MBO}=90^0\)
hay MB là tiếp tuyến của (O)
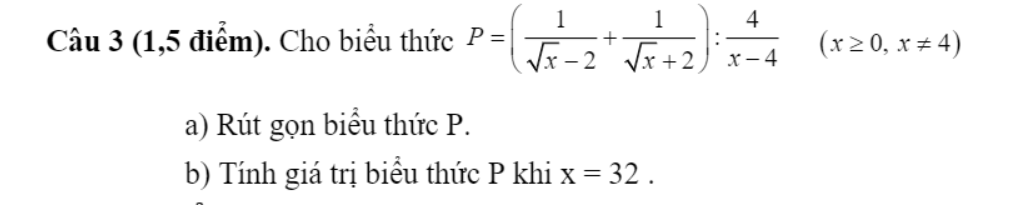
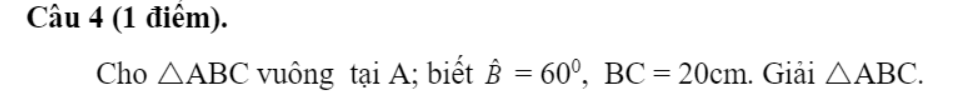






a: \(P=\dfrac{\sqrt{x}+2+\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\cdot\dfrac{x-4}{4}=\dfrac{\sqrt{x}}{2}\)