Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+) Dễ có tam giác OAB đồng dạng với tam giác ODC (góc AOB = DOC do đối đỉnh; góc BAC = BDC do góc nội tiếp cùng chắn cung BC)
=> \(\frac{OA}{OD}=\frac{OB}{OC}=\frac{AB}{DC}=\frac{a}{c}\)
+) Tương tự, tam giác OAD đồng dạng với tam giác OBC (g - g)
=> \(\frac{OA}{OB}=\frac{OD}{OC}=\frac{AD}{BC}=\frac{b}{d}\)
+) Ta có: \(\frac{OB}{OC}+\frac{OD}{OC}=\frac{a}{c}+\frac{b}{d}=\frac{ad+bc}{cd}\)=> \(\frac{OB+OD}{OC}=\frac{BD}{OC}=\frac{ad+bc}{cd}\Rightarrow\frac{OC}{BD}=\frac{cd}{ad+bc}\) (1)
+) ta có: \(\frac{OA}{OD}=\frac{a}{c};\frac{OA}{OB}=\frac{b}{d}\Rightarrow\frac{OD}{OA}=\frac{c}{a};\frac{OB}{OA}=\frac{d}{b}\)
=> \(\frac{OD}{OA}+\frac{OB}{OA}=\frac{BD}{OA}=\frac{c}{a}+\frac{d}{b}=\frac{bc+ad}{ab}\Rightarrow\frac{OA}{BD}=\frac{ab}{bc+ad}\)(2)
Từ (1)(2) => \(\frac{OC}{BD}+\frac{OA}{BD}=\frac{cd+ab}{ad+bc}\Rightarrow\frac{AC}{BD}=\frac{ab+cd}{ad+bc}\)


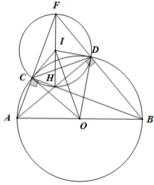
a) Vì C, D thuộc nửa đường tròn đường kính AB nên
A C B = A D B = 90 o ⇒ F C H = F D H = 90 o ⇒ F C H + F D H = 180 o
Suy ra tứ giác CHDF nội tiếp
b) Vì AH ⊥ BF, BH ⊥ AF nên H là trực tâm ∆ AFB ⇒ FH ⊥ AB
⇒ C F H = C B A ( = 90 o − C A B ) ⇒ Δ C F H ~ Δ C B A ( g . g ) ⇒ C F C B = C H C A ⇒ C F . C A = C H . C B

a) Xét ΔOCD có OC=OD(=R)
nên ΔOCD cân tại O(Định nghĩa tam giác cân)
Xét ΔOCD cân tại O có CD=OC(=R)
nên ΔOCD đều(Dấu hiệu nhận biết tam giác đều)
\(\Leftrightarrow\widehat{COD}=60^0\)
hay \(sđ\stackrel\frown{CD}=60^0\)