
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b) Ta có: \(\sqrt{150}-\sqrt{1.6}\cdot\sqrt{60}+4.5\cdot\sqrt{2\dfrac{2}{3}}-\sqrt{6}\)
\(=5\sqrt{6}-4\sqrt{6}-\sqrt{6}+\dfrac{9}{2}\cdot\sqrt{\dfrac{8}{3}}\)
\(=\dfrac{9}{2}\cdot\dfrac{2\sqrt{2}}{\sqrt{3}}\)
\(=3\sqrt{6}\)
\(\sqrt{150}+\sqrt{1,6}.\sqrt{60}+4.5\sqrt{2\dfrac{2}{3}}-\sqrt{6}\\ =5\sqrt{6}+4\sqrt{6}+3\sqrt{6}-\sqrt{6}\\ =11\sqrt{6}\)


Câu 15:
Hàm số y=ax+b, với a<>0 nghịch biến trên R khi a<0
Từ đó bạn thay vào thôi
Câu 14:
Bạn cần biến đổi về dạng y=ax+b(a<>0) rồi sau đó lần lượt thay x=0 và y=0 vào là ra

Điều kiện:`a>=0,a ne 1` $\\$ `E=(1+(a-sqrta)/(sqrta-1))(1-(a+sqrta)/(1+sqrta))`
`=(1+(sqrta(sqrta-1))/(sqrta-1))(1-(sqrta(sqrta+1))/(sqrta+1))`
`=(1+sqrta)(1-sqrta)`
`=1-a`
\(E=\left(1+\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\right)\left(1-\dfrac{a+\sqrt{a}}{1+\sqrt{a}}\right)\)
ĐK: a ≥ 0; a khác 1
\(=\left[1+\dfrac{\sqrt{a}\left(\sqrt{a}-1\right)}{\sqrt{a}-1}\right]\left[1-\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)}{\sqrt{a}+1}\right]\)
\(=\left(1+\sqrt{a}\right)\left(1-\sqrt{a}\right)=1-a\)

1: góc DMB+góc DHB=180 độ
=>DMBH nội tiếp
2: Kẻ tiếp tuyến Ax của (O)
=>góc xAC=góc ABC
góc AMD+góc AND=180 độ
=>AMDN nội tiếp
=>góc ANM=góc ADM=góc ABH
=>góc ANM=góc xAC
=>Ax//MN

Do (d) đi qua E và G nên thay tọa độ E và G vào pt (d) ta được:
\(\left\{{}\begin{matrix}a.1+b=-3\\a.\left(-2\right)+b=6\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a+b=-3\\-2a+b=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3a=-9\\-2a+b=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-3\\b=0\end{matrix}\right.\)
Vậy pt (d) là: \(y=-3x\)

1.
$(m^2-m-1)x-5m=(3-m)x$
$\Leftrightarrow (m^2-m-1+m-3)x=5m$
$\Leftrightarrow (m^2-4)x=5m$
$\Leftrightarrow (m-2)(m+2)x=5m$
Nếu $m=-2$ thì $0x=-10$ (vô lý) $\Rightarrow$ pt vô nghiệm
Nếu $m=2$ thì $0x=10$ (vô lý) $\Rightarrow$ pt vô nghiệm
Nếu $m\neq \pm 2$ thì pt có nghiệm duy nhất $x=\frac{5m}{(m-2)(m+2)}$
2.
$m^2x+mx+x-m-2=0$
$\Leftrightarrow x(m^2+m+1)=m+2$
Vì $m^2+m+1=(m+\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}>0$ với mọi $m\in\mathbb{R}$
$\Rightarrow m^2+m+1\neq 0$
Do đó pt có nghiệm duy nhất $x=\frac{m+2}{m^2+m+1}$ với mọi $m\in\mathbb{R}$

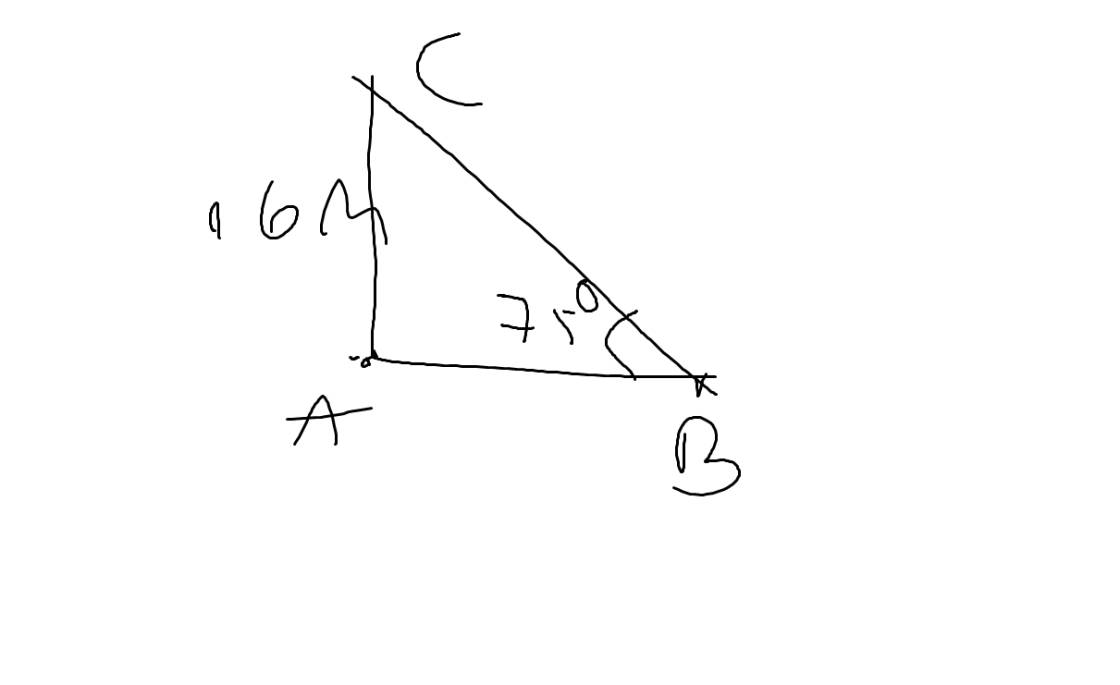
Gọi A,B lần lượt là hai mốc của bờ sông. Gọi điểm C là điểm nằm trên đường thước dây vuông góc với bờ sông tại A
=>AB vuông góc AC tại A
Theo đề, ta có: AC=16m \(\widehat{ABC}=75^0\)
Xét ΔABC vuông tại A có \(tanB=\dfrac{AC}{AB}\)
=>\(AB=\dfrac{AC}{tanB}=16:tan75\simeq4,3\left(m\right)\)

\(\dfrac{1}{2+\sqrt{3}}+\dfrac{1}{2-\sqrt{3}}\\ =\dfrac{2-\sqrt{3}}{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}+\dfrac{2+\sqrt{3}}{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}\\ =\dfrac{2-\sqrt{3}+2+\sqrt{3}}{2^2-\left(\sqrt{3}\right)^2}\\ =\dfrac{2+2}{4-3}\\ =4\)
Ta có: \(\dfrac{1}{2+\sqrt{3}}+\dfrac{1}{2-\sqrt{3}}\)
\(=2-\sqrt{3}+2+\sqrt{3}\)
=4
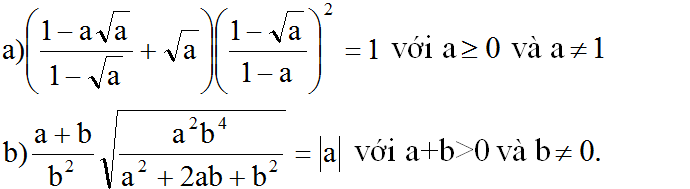
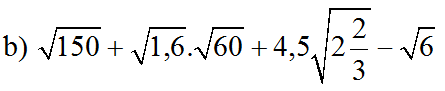

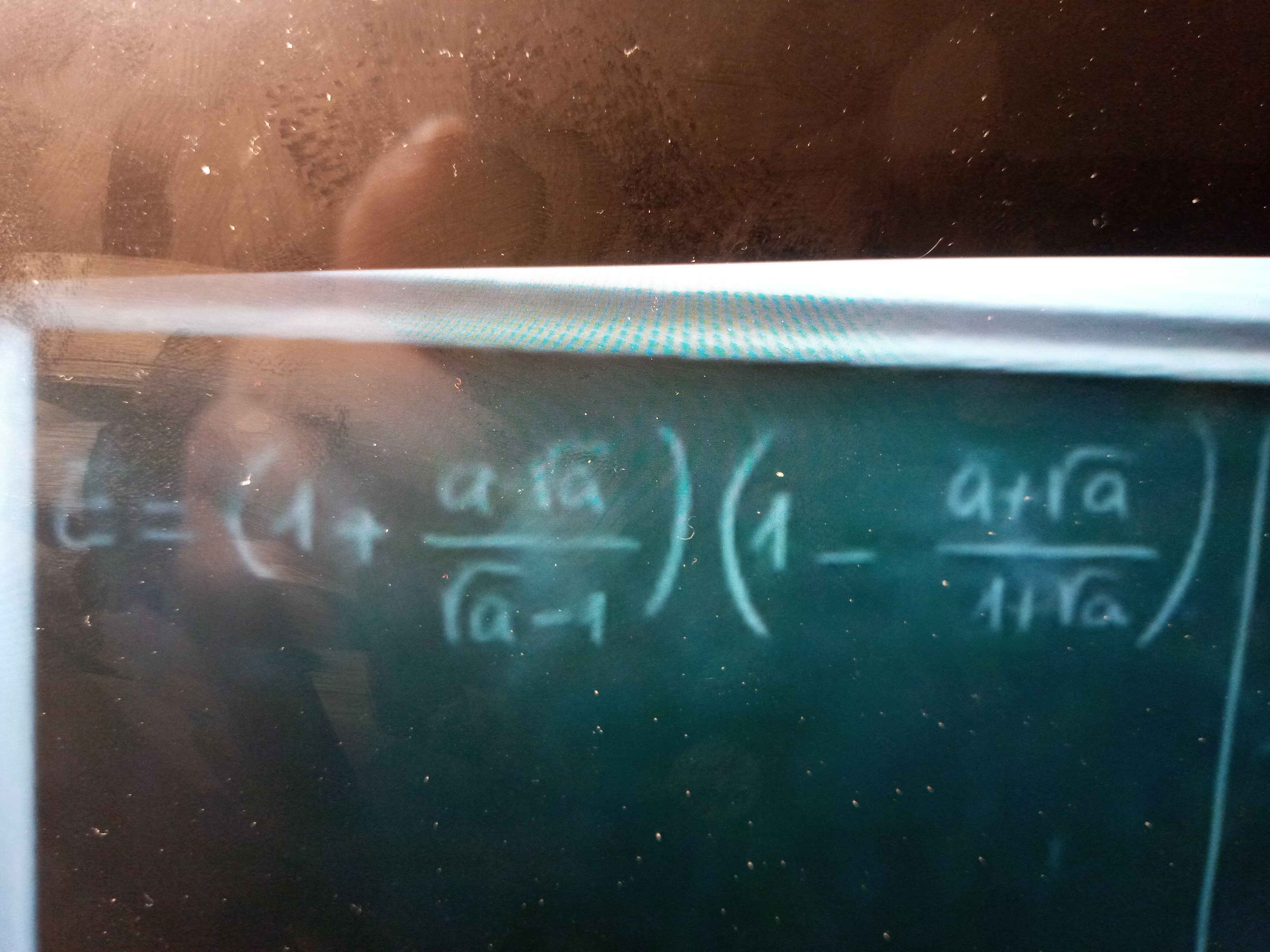




a) Ta có: \(\left(\dfrac{1-a\sqrt{a}}{1-\sqrt{a}}+\sqrt{a}\right)\left(\dfrac{1-\sqrt{a}}{1-a}\right)^2\)
\(=\left(a+2\sqrt{a}+1\right)\cdot\left(\dfrac{1}{\sqrt{a}+1}\right)^2\)
\(=1\)
b) Ta có: \(\dfrac{a+b}{b^2}\cdot\sqrt{\dfrac{a^2b^4}{a^2+2ab+b^2}}\)
\(=\dfrac{a+b}{b^2}\cdot\dfrac{\left|a\right|\cdot b^2}{a+b}\)
=|a|