
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Mình nghĩ là không tồn tại , số chính phương hay ta có thể gọi nó là lũy thừa căn bậc 2 của 1 số , mà đây ta có các chữ số đều giống nhau , không thể thực hiên .
Các chữ số giống nhau nên nếu a có tồn tại thì a sẽ là các chữ số từ 1 - 9 ( a không thể là 0 )
mà các số đều dư khi sử dụng căn bậc \(\sqrt{ }\)
nên không có bất cứ số a nào thỏa mãn đề bài


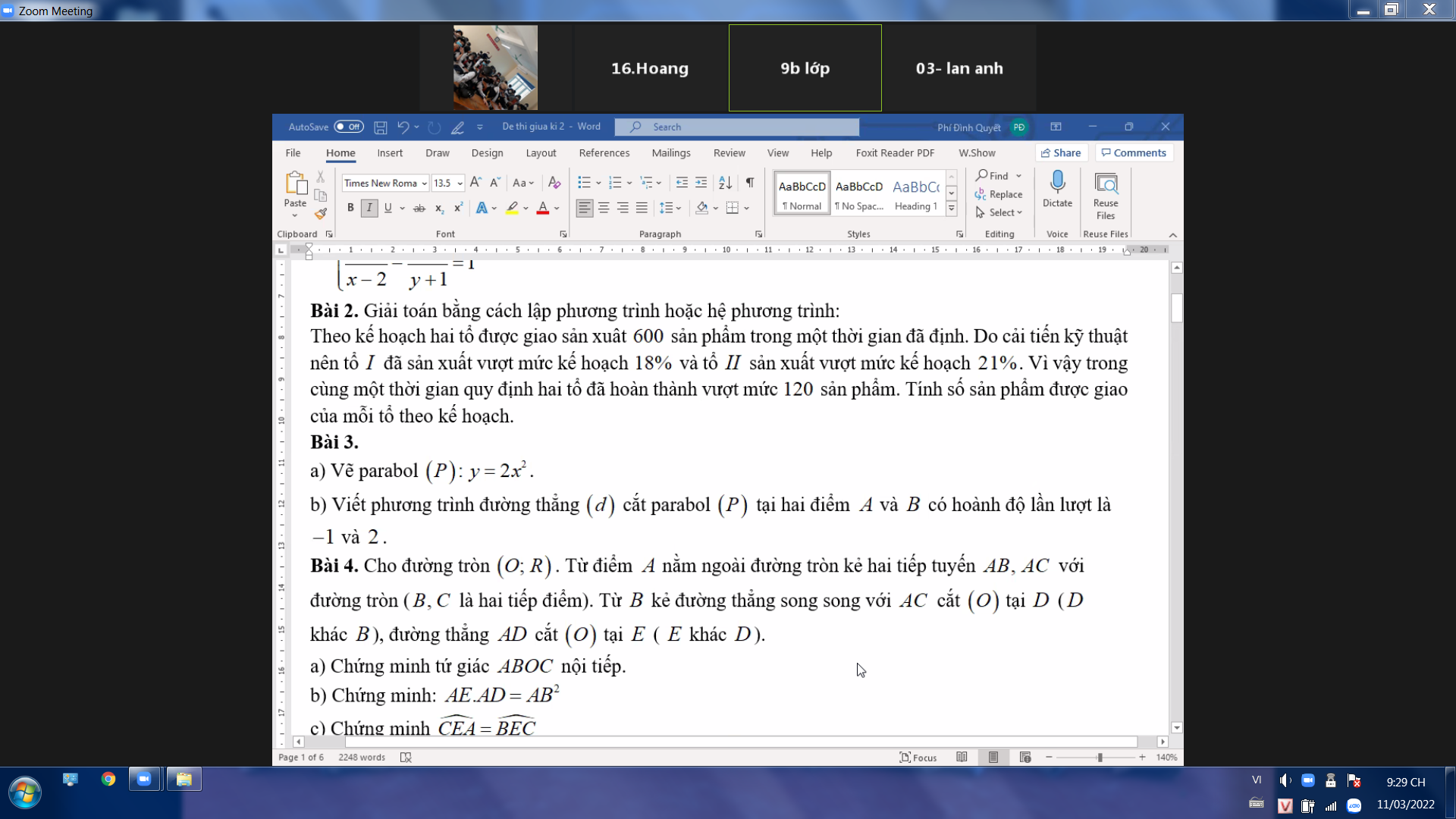
1.
a. Ta có: \(AB^2+AC^2=6^2+8^2=36+64=100\)
\(BC^2=10^2=100\)
\(\Rightarrow AB^2+AC^2=BC^2\) \(\Rightarrow\Delta\)ABC vuông tại A
b. \(\Delta\)ABC vuông tại A, đường cao AH. Ta có:
AB.AC = AH.BC
hay 6.8 = AH.10
=> AH = \(\dfrac{6.8}{10}=4.8\)

4: \(=\dfrac{x-3\sqrt{x}+2-x-4\sqrt{x}-3-x-5}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{-x-7\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{-\left(\sqrt{x}+1\right)\left(\sqrt{x}+6\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}=\dfrac{-\sqrt{x}-6}{\sqrt{x}-2}\)
5: \(=\dfrac{x-4\sqrt{x}+3-\left(2x-5\sqrt{x}+2\right)+x-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{2x-4\sqrt{x}+1-2x+5\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\sqrt{x}-1}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}=\dfrac{1}{\sqrt{x}-2}\)
6: \(=\dfrac{x+2+x-1-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}=\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\)
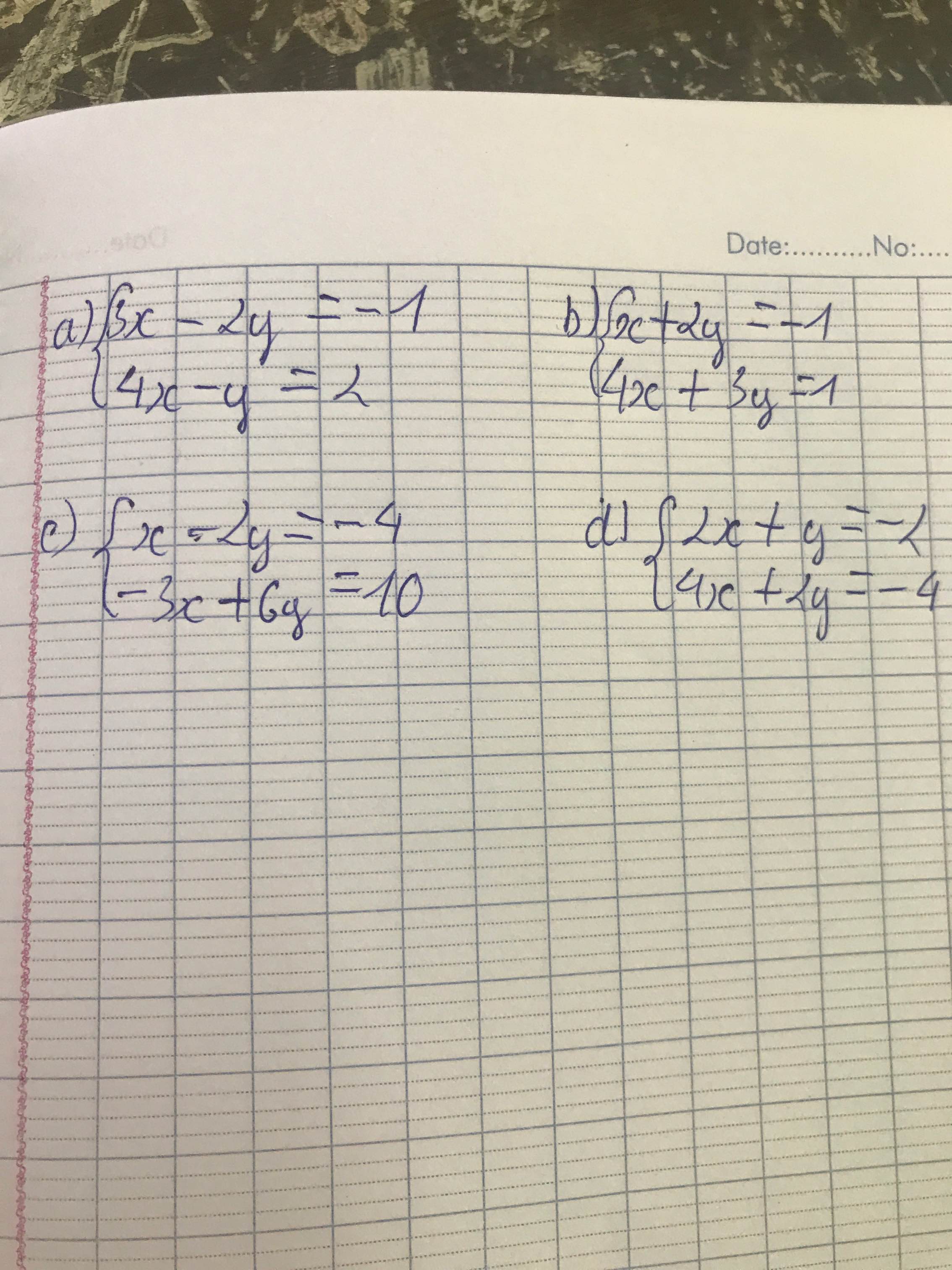
 Mình giải được câu a) và b) rồi . Mọi người giúp c) và d) nhé ! (Ưu tiên gải câu c , không giải câu d cũng được ) Cảm ơn!
Mình giải được câu a) và b) rồi . Mọi người giúp c) và d) nhé ! (Ưu tiên gải câu c , không giải câu d cũng được ) Cảm ơn!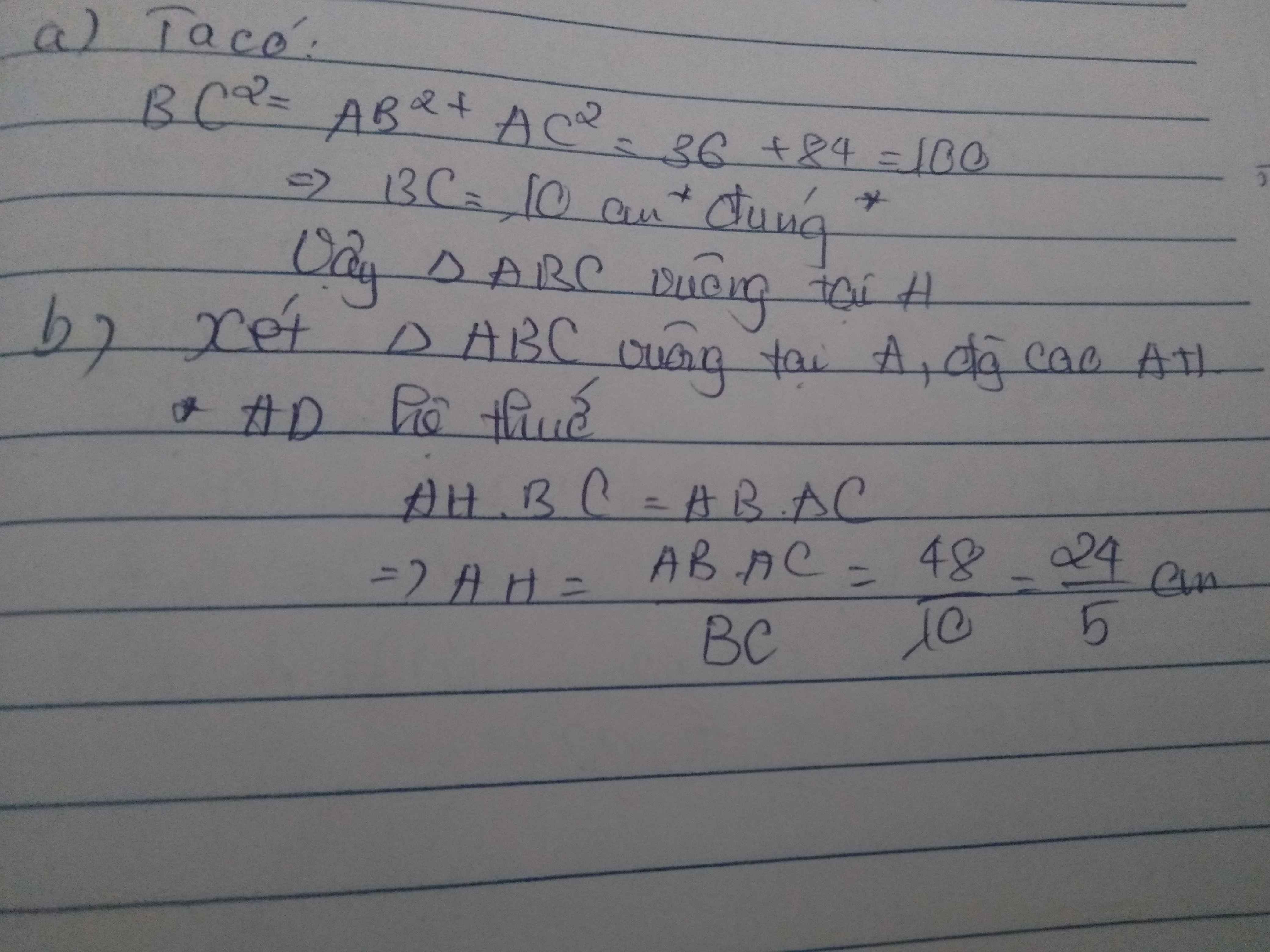
 Giúp mình nhé !!!
Giúp mình nhé !!!
a: \(\Leftrightarrow\left\{{}\begin{matrix}3x-2y=-1\\8x-2y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-5x=-5\\4x-y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
b: \(\Leftrightarrow\left\{{}\begin{matrix}4x+8y=-4\\4x+3y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5y=-5\\x+2y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-1\\x=1\end{matrix}\right.\)
c: \(\Leftrightarrow\left\{{}\begin{matrix}3x-6y=-12\\-3x+6y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}0x=-2\left(loại\right)\\-3x+6y=10\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\varnothing\)
d: \(\Leftrightarrow\left\{{}\begin{matrix}2x+y=-2\\2x+y=-2\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in R\)
\(a,\left\{{}\begin{matrix}3x-2y=-1\\4x-y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-2\left(4x-2\right)=-1\\y=4x-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-8x+4=-1\\y=4x-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-5x=-5\\y=4x-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=4.1-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
\(b,\left\{{}\begin{matrix}x+2y=-1\\4x+3y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1-2y\\4\left(-1-2y\right)+3y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1-2y\\-4-8y+3y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1-2y\\-5y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1-2\left(-1\right)\\y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)
\(c,\left\{{}\begin{matrix}x-2y=-4\\-3x+6y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2y-4\\-3\left(2y-4\right)+6y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2y-4\\-6y+12+6y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2y-4\\12=10\left(vô.lí\right)\end{matrix}\right.\)
\(d,\left\{{}\begin{matrix}2x+y=-2\\4x+2y=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+y=-2\\2x+y=-2\left(luôn.đúng\right)\end{matrix}\right.\)