NN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 8 2020
1.
\(y=2\left(\frac{1}{2}sinx-\frac{\sqrt{3}}{2}cosx\right)=2sin\left(x-\frac{\pi}{3}\right)\)
\(sin\left(x-\frac{\pi}{3}\right)\le1\) ;\(\forall x\Rightarrow y\le2\) ;\(\forall x\)
\(y_{max}=2\) khi \(sin\left(x-\frac{\pi}{3}\right)=1\)
2.
\(y=5\left(\frac{3}{5}sinx+\frac{4}{5}cosx\right)\)
Đặt \(\frac{3}{5}=cosa\) với \(a\in\left(0;\pi\right)\)
\(\Rightarrow y=5\left(sinx.cosa+cosx.sina\right)=5sin\left(x+a\right)\)
\(-1\le sin\left(x+a\right)\le1\Rightarrow-5\le y\le5\)
\(y_{min}=-5\) ; \(y_{max}=5\)
PT
1
TA
19 tháng 12 2020
\(y=\dfrac{3sinx-cosx-4}{2sinx+cosx-3} \Leftrightarrow (2sinx+cosx-3)y=3sinx-cosx-4 \Leftrightarrow (3-2y)sinx+(y-1)cosx=4-3y \)
\(\Rightarrow (3-2y)^2+(y-1)^2 ≥ (4-3y)^2 \Leftrightarrow 5y^2−14y+10 ≥ 16−24y+9y^2 \Leftrightarrow 1 ≤ y ≤ \dfrac{3}{2}\)
Vậy hàm số không có giá trị nguyên.
PT
1
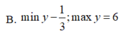
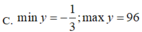
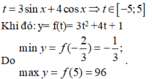
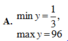
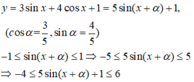
\(y=cosx-3.sinx\le\sqrt{\left(1+\left(-3\right)^2\right)\left(cos^2x+sin^2x\right)}=\sqrt{10}\)
\(\Rightarrow y_{max}=\sqrt{10}\)