

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn B
Vì y = a x 3 + c x + d , a ≠ 0 là hàm số bậc ba và có m i n x ∈ - ∞ ; 0 f ( x ) = f ( - 2 ) nên a < 0 và y' = 0 có hai nghiệm phân biệt.
Ta có ![]() có hai nghiệm phân biệt
⇔
ac < 0
có hai nghiệm phân biệt
⇔
ac < 0
Vậy với a < 0, c > 0 thì y' = 0 có hai nghiệm đối nhau 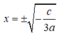
Từ đó suy ra
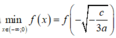
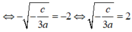
⇔
c = -12a
Ta có bảng biến thiên
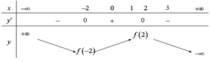
Ta suy ra ![]()

Ta có bảng biến thiên như hình vẽ sau:
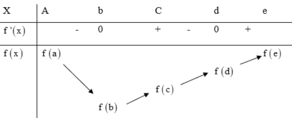
Giá trị nhỏ nhất của hàm số là f( b) nhưng giá trị lớn nhất có thể là f (a) hoặc f( e) Theo giả thiết ta có: f(a) + f( c)) = f( b) + f( d) nên f(a) - f( d)) = f( b) - f( c)< 0
Suy ra : f( a) < f( d) < f( e)
Vậy m a x [ a ; e ] f ( x ) = f ( e ) ; m i n [ a ; e ] f ( x ) = f ( b )
Chọn C.

Chọn B
Ta có 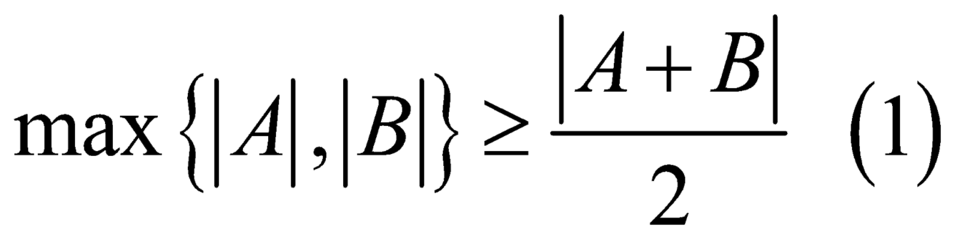 .
.
Dấu = xảy ra khi A=B.
Ta có 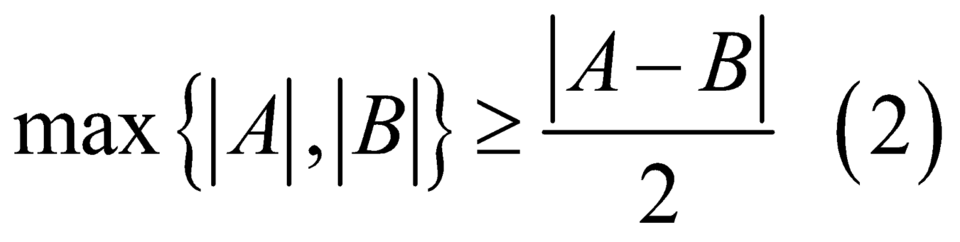 .
.
Dấu = xảy ra khi A= -B.
Xét hàm số ![]() , có
, có ![]() .
.
Trường hợp 1: ![]()
![]() .
.
Khi đó ![]() .
.
Áp dụng bất đẳng thức (1) ta có ![]() .
.
Trường hợp 2: ![]()
![]() .
.
Khi đó  .
.
Áp dụng bất đẳng thức (1) và(2) ta có
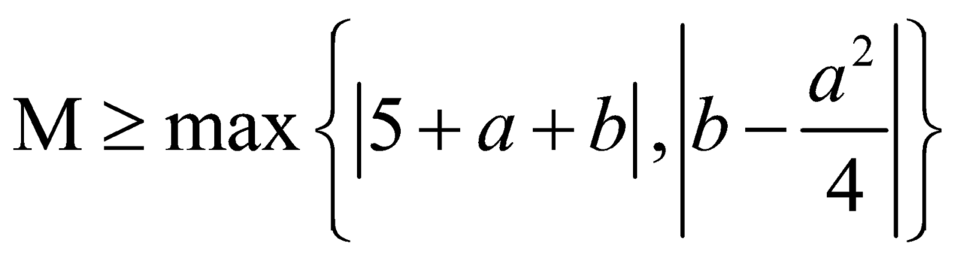
![]()
![]() .
.
Suy ra ![]() .
.
Vậy M nhận giá trị nhỏ nhất ![]() khi
khi
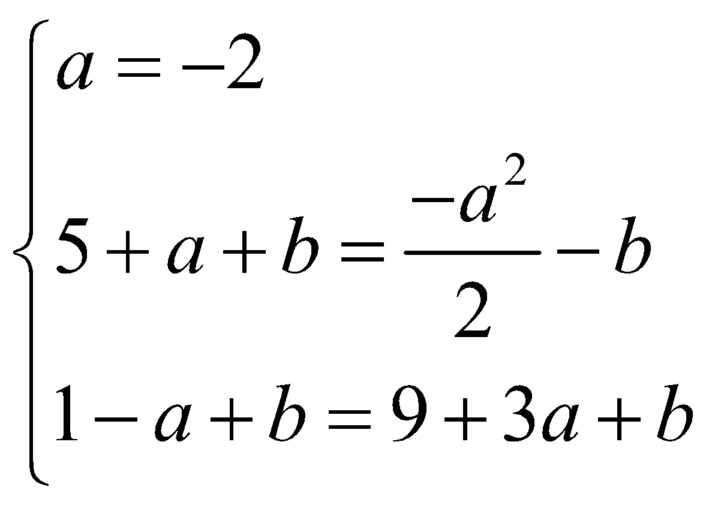
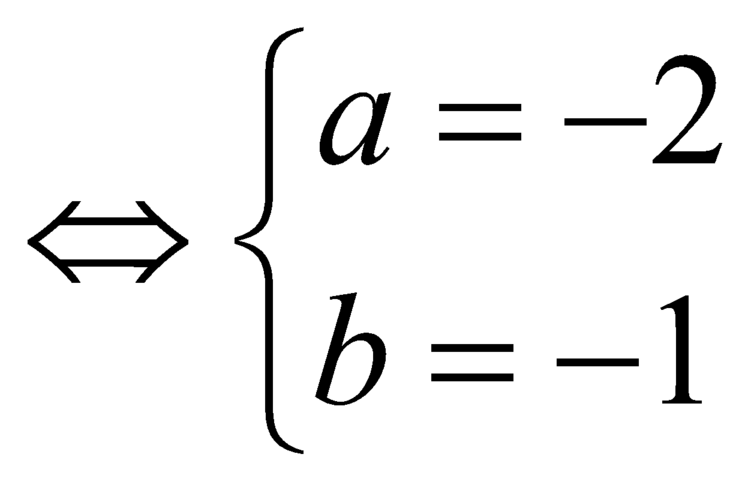 .
.
Do đó ![]() .
.

Đáp án D
Phương pháp:
Dựa vào đồ thị hàm số ta xác định được điểm cao nhất và điểm thấp nhất của đồ thị trên đoạn [-1;3]
Tung độ điểm cao nhất là giá trị lớn nhất của hàm số, tung độ điểm thấp nhất là giá trị nhỏ nhất của hàm số trên đoạn [-1;3].
Từ đó ta tìm được: M;m => M-m
Cách giải:
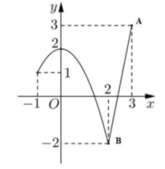
Từ đồ thị hàm số ta thấy trên đoạn [-1;3] thì điểm cao nhất của đồ thị là điểm A(3;3) và điểm thấp nhất của đồ thị là B(2;-2) nên GTLN của hàm số là M=3 và GTNN của hàm số là m = -2
Từ đó M - m = 3 - (-2) = 5

Chọn A
+ Từ đồ thị của đạo hàm ta lập được bảng biến thiên như sau
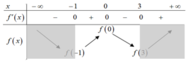
+ Dựa vào BBT ta suy ra giá trị lớn nhất của hàm số trên đoạn [-1;3] là f(0)

Chọn C
Xét hàm số f(x) = | x 2 + a x + b |. Theo đề bài, M là giá trị lớn nhất của hàm số trên [-1;3]
Suy ra
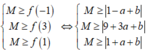
![]()
![]()
![]()
Nếu M = 2 thì điều kiện cần là ![]() và
và ![]() cùng dấu
cùng dấu
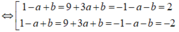
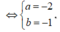
Ngược lại, khi 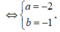
Ta có, hàm số ![]()
![]()
M là giá trị lớn nhất của hàm số f(x) trên [-1;3] ![]()
Vậy 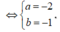
Ta có: a + 2b = -4.