Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng bất đẳng thức |m|+ |n|≥ |m + n| .Dấu = xảy ra khi m,n cùng dấu
A ≥ |x − a + x − b|+ |x − c + x − d| = |2x − a − b|+ |c + d − 2x| ≥ |2x − a − b − 2x + c + d| =|c + d − a − b|
Dấu = xảy ra khi x − a và x − b cùng dấu hay(x ≤ a hoặc x ≥ b)
x − c và x − d cùng dấu hay(x ≤ c hoặc x ≥ d)
2x − a − b và c + d − 2x cùng dấu hay (x + b ≤ 2x ≤ c + d)
Vậy Min A =c+d-a-b khi b ≤ x ≤ c
~ Học tốt ~ K cho mk nha. Thank you.

a) \(\Rightarrow\left(x-3\right)\left(x+4\right)=5.12\)
\(\Rightarrow x^2+x-72=0\)
\(\Rightarrow\left(x-8\right)\left(x+9\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=8\\x=-9\end{matrix}\right.\)
b) \(\Rightarrow\left(x+3\right)^2=36\)
\(\Rightarrow\left[{}\begin{matrix}x+3=6\\x+3=-6\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=3\\x=-9\end{matrix}\right.\)
c) \(\Rightarrow2x^2=8\Rightarrow x^2=4\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)

Gấp thì giúp đây ^_^ !!
+) Ta có : AM = BM ; M thuộc cạnh huyền BC
=> AM là đường trung tuyến ứng với cạnh huyền BC
=> AM = BM = MC
+) \(\widehat{BAC}+\widehat{B}+\widehat{C}=180^o\)
\(\Leftrightarrow90^o+30^o+\widehat{C}=180^o\)
\(\Leftrightarrow\widehat{C}=60^o\)
Xét tam giác AMC có :
\(\hept{\begin{cases}\widehat{C}=60^o\\AM=MC\end{cases}}\)
=> AMC là tam giác đều ( đpcm )

Theo đề bài ta có:
;
cân bằng phương trình bằng cách nhân x vào cả hai vế ta có:
cân bằng phương trình bằng cách nhân y vào cả hai vế ta có:
cân bằng phương trình bằng cách nhân z vào cả hai vế ta có:
vì
Vì Có cùng số mũ và bằng nhau
Nên các cơ số cũng bằng nhau
Ta có: \(x^2=y\cdot z\)
nên \(z=\dfrac{x^2}{y}\)(1)
Ta có: \(y^2=z\cdot x\)
nên \(z=\dfrac{y^2}{x}\)(2)
Từ (1) và (2) suy ra \(\dfrac{x^2}{y}=\dfrac{y^2}{x}\)
\(\Leftrightarrow x^3=y^3\)
hay x=y(3)
Ta có: \(x^2=y\cdot z\)
nên \(y=\dfrac{x^2}{z}\)(4)
Ta có: \(z^2=x\cdot y\)
nên \(y=\dfrac{z^2}{x}\)(5)
Từ (4) và (5) suy ra \(\dfrac{x^2}{z}=\dfrac{z^2}{x}\)
\(\Leftrightarrow x^3=z^3\)
hay x=z(6)
Từ (3) và (6) suy ra x=y=z(đpcm)

đúng rồi ạ, giúp em với ạ hoặc làm đc câu nào giúp em cũng được ạ

Ta có \(A= \left|x-3\right|+\left|x+7\right|+\left|x+1\right|=\left(\left|x-3\right|+\left|x+7\right|\right)+\left|x+1\right|\)
\(=\left(\left|3-x\right|+\left|x+7\right|\right)+\left|x+1\right|\)
Ta thấy \(\left|3-x\right|+\left|x+7\right|\ge\left|3-x+x+7\right|=10\)
Dấu bằng xảy ra khi và chỉ khi \(\left(3-x\right).\left(x+7\right)\ge0\Leftrightarrow-7\le x\le3\)
Mà \(\left|x+1\right|\ge0\)nên \(A=\left|x-3\right|+\left|x+7\right|+\left|x+1\right|\ge0+4=4\)
Dấu bằng xảy ra khi và chỉ khi \(-7\le x\le3\)
Vậy GTNN của A là 4 khi và chỉ khi \(-7\le x\le3\)
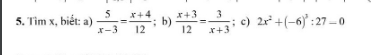
\(\frac{12}{99}\)x9+90/99
giải bình thường!